Liebe Datenanalysten,

was gut ist, kommt wieder, besagt ein geflügeltes Wort. Das wollen wir hoffen! In den Sechzigerjahren beispielsweise war es fast selbstverständlich, dass man betriebswirtschaftliche Statistiken über Umsätze, Preise, Kosten und vieles andere mit einer logarithmischen Achsenskalierung zeichnete. Wie sonst hätte man prozentuale Veränderungen, auf die es ankam, dem Diagramm entnehmen können? Damals war die Datenaufbereitung arbeitsintensiv, das Zeichnen mühsam, spezielle Arbeitsmittel wie Logarithmenpapier waren nötig. Durch Software ist vieles einfacher geworden, Logarithmenpapier wird heute nicht mehr hergestellt. Mit neuen Technologien scheinen jedoch einige bewährte Methoden in Vergessenheit geraten zu sein. Wenn wir in Seminaren und Vorträgen dafür plädieren, ebendiese logarithmischen Skalen verstärkt zu verwenden, weil nur sie die prozentualen Veränderungen vergleichbar machen, schlägt uns immer wieder eine gewisse Skepsis, ja Unbehagen entgegen. Mit diesen clicks! möchten wir Ihnen zeigen, warum der Logarithmus so wichtig ist und dass Sie dank DeltaMaster mühelos damit umgehen können. Auf dass die logarithmische Skala bald wiederkommt: Weil sie gut ist. Für aussagekräftige Berichte ebenso wie für unsere Informationskultur im Allgemeinen.

Herzliche Grüße
Ihr Team von Bissantz & Company

Es klingt unglaublich: Viele Zeitreihendarstellungen, die uns tagtäglich in Controllingberichten und in den Medien begegnen, sind verzerrt – so verzerrt, dass wir nicht mehr richtig einschätzen können, was uns an der Darstellung eigentlich interessiert: die relativen (prozentualen) Wertänderungen.

Schuld daran ist die herkömmliche, lineare Skalierung der Y-Achse. In einem Liniendiagramm lässt sie dieselbe prozentuale Veränderung mal mehr, mal weniger steil erscheinen. Dadurch sind die Steigungswinkel im Diagramm nicht vergleichbar. Die Lösung ist vergleichsweise einfach – aber, so haben wir es immer wieder erlebt, nicht ganz einfach durchzusetzen: Mit einer logarithmischen Skala werden die Steigungen zwischen zwei Zeiteinheiten vergleichbar. Allerdings erscheint „logarithmisch“ vielen Berichtsempfängern etwas unheimlich. Deshalb möchten wir Ihnen in diesen DeltaMaster clicks! vor allem Argumente an die Hand geben, wann und warum die logarithmische Skalierung so wichtig ist. Damit sind Sie gerüstet für Diskussionen und Rückfragen und können sich wirkungsvoll einsetzen für die bessere und nicht selten: die einzig richtige Visualisierung. Daneben erläutern wir natürlich, wie man das in DeltaMaster umsetzt. Sie werden sehen: Logarithmisch zu skalieren, ist ganz einfach.

Trugschlüsse bei linearer Achsenskalierung

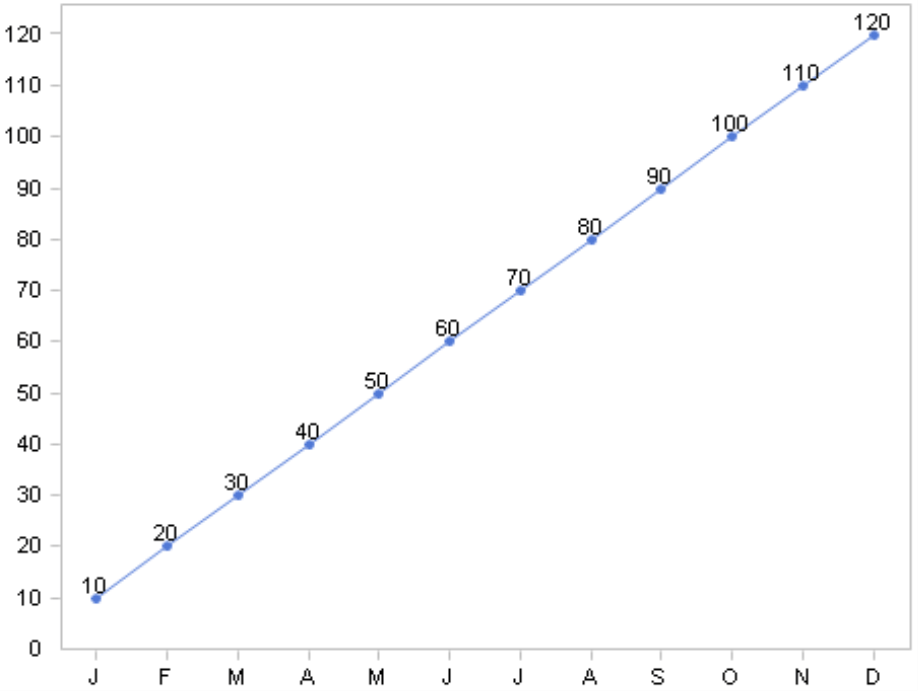
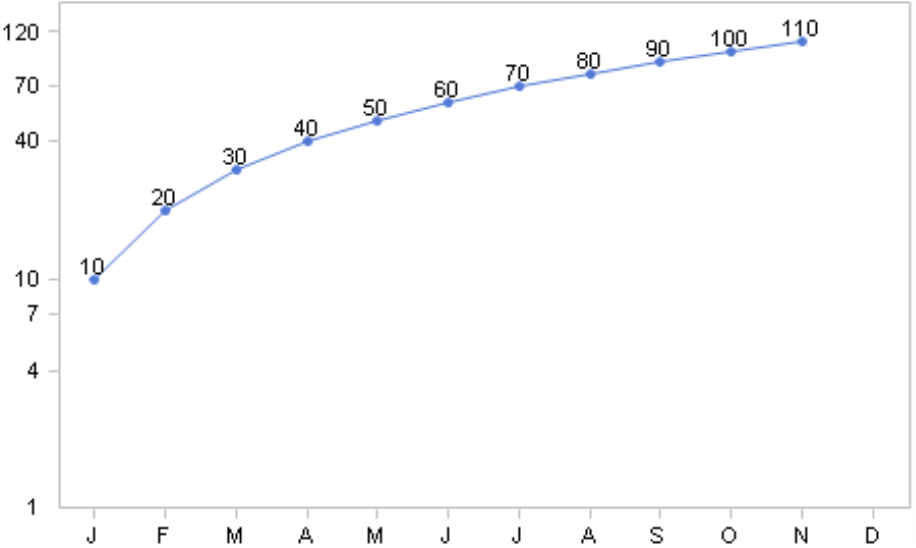
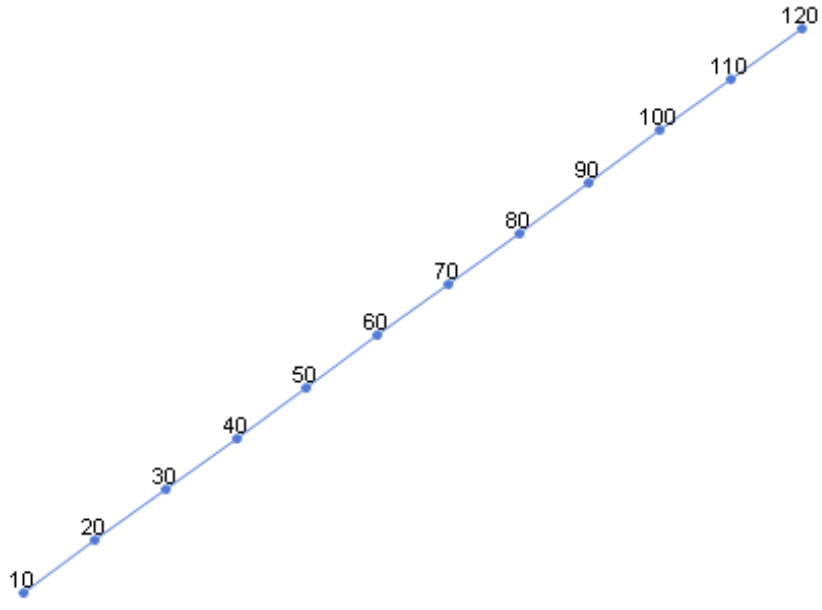
Um zu demonstrieren, wie sehr die übliche Achsenskalierung verzerrt, wenn es um relative Veränderungen geht, haben wir ein kleines Beispiel konstruiert. Unser Modell enthält einen Analysewert, zum Beispiel einen Aktienkurs oder den Umsatz, und eine Zeitdimension mit 12 Elementen – Kalendermonaten, die wir abkürzend „J“, „F“, „M“ usw. genannt haben. Die Zeitreihe beginnt im Januar mit einem Wert von 10. Dieser wächst jeden Monat um 10, sodass wir im Dezember auf 120 kommen. Die nebenstehende Abbildung zeigt diese Wertentwicklung im Modul Zeitreihenanalyse von DeltaMaster. Die Linie sieht aus, wie jedermann es erwarten würde: Eine Gerade von links unten nach rechts oben, der Steigungswinkel der Linienabschnitte zwischen zwei Monaten ist immer derselbe. Das legt den Schluss nahe: Der Wert ist schön gleichmäßig gewachsen, wir sind auf einem guten Kurs.

Ist das wirklich so? Nicht, wenn es auf die relativen Veränderungen ankommt!

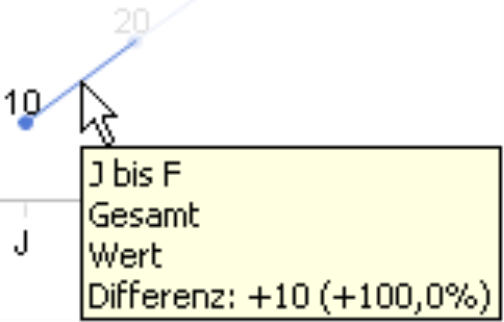
Die lassen sich einfach abrufen: Wenn Sie in DeltaMaster mit der Maus auf einen Linienabschnitt zeigen, werden die absolute und die prozentuale Veränderung in einem „Tooltipp“ eingeblendet.

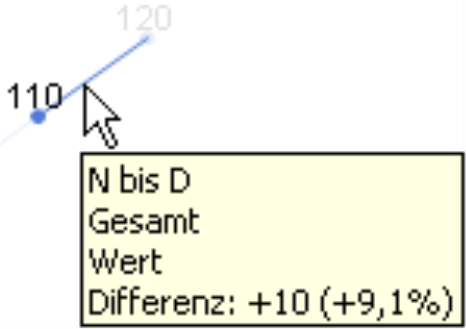
Die gleiche Steigung steht einmal für 100 % Veränderung (von 10 auf 20) und einmal für nur 9,1 % (von 110 auf 120). In der Grafik ist von diesem gewaltigen Unterschied nichts zu erkennen. Bei der Analyse von relativen Veränderungen führt uns die lineare Skala in die Irre, denn der gleiche Steigungswinkel kann für ganz unterschiedliche Wertentwicklungen stehen, je nachdem, wie klein oder groß der Vergleichswert des Vormonats ist. Und umgekehrt kann die gleiche relative Änderung zwischen zwei benachbarten Zeitpunkten im selben Diagramm einmal sehr steil, einmal sehr flach erscheinen, wiederum abhängig vom Startwert.

Angesichts dieses eklatanten Mangels der linearen Skalierung verwundert es, dass sie so etabliert ist: In wirtschaftlichen Fragen, etwa wenn von Wachstum die Rede ist, geht es schließlich fast immer um relative Veränderungen. Es ist eine Binsenweisheit, dass wir einen Änderungsbetrag nur dann richtig beurteilen können, wenn wir den Ausgangswert kennen. Das leisten die herkömmlichen Diagramme aber nicht, wie wir oben gesehen haben: Eine Steigerung von 10 auf 20 Euro sieht grafisch genauso aus wie die von 110 auf 120 Euro oder von 1.000 auf 1.010 Euro. Eine solche Grafik verschleiert, wo sich tatsächlich etwas bewegt hat und wo ein einmal erreichter Wert nur mehr oder weniger gehalten wurde.

Vergleichbarkeit durch logarithmische Skala

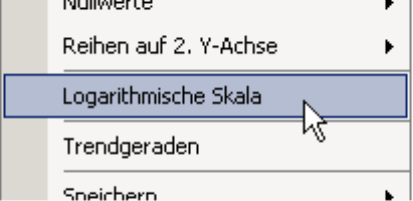
Die Lösung für dieses Problem ist denkbar einfach, auch wenn sie nicht so klingt: Wir skalieren die Y-Achse logarithmisch. Dadurch wird die gleiche prozentuale Wertänderung immer als die gleiche Steigung im Diagramm dargestellt. In DeltaMaster aktivieren Sie die logarithmische Skala über das Kontextmenü oder das Menü Ich möchte in der Zeitreihenanalyse.

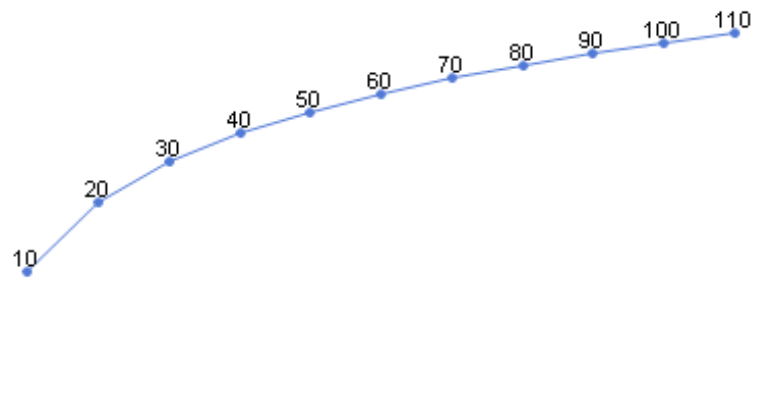
Damit sieht der Graph aus, wie hier gezeigt. Die Linie beginnt jetzt mit einem steilen Anstieg, der für die große Veränderung von 100 % steht, von 10 auf 20. Danach verläuft die Linie immer flacher, denn prozentual gesehen nimmt auch der Wert immer weniger zu. Den geringen Anstieg am Ende (um 9,1 %, von 110 auf 120) können wir jetzt auch als solchen erkennen. Die abnehmenden Abstände zwischen den Teilungen auf der Y-Achse sind charakteristisch für logarithmische Skalen.

Gleiche Steigung, gleiche Änderung

Ein zweites Beispiel: der Aktienkurs von Infineon. Wir haben den Zeitraum von Dezember 2007 bis Februar 2009 erhoben, mit DeltaMaster ImportWizard in einem OLAP-Würfel umgesetzt und mit DeltaMaster ausgewertet.
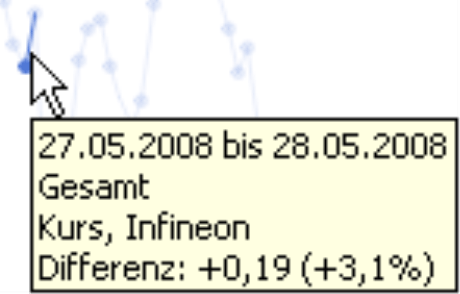
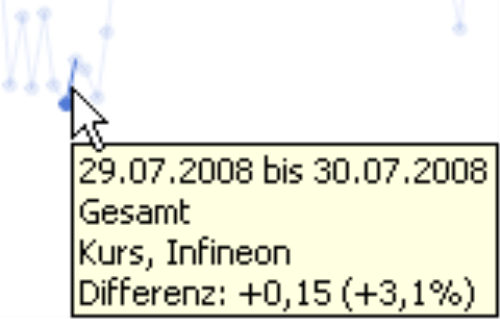
Werfen wir zunächst einen Blick auf Details: Im betrachteten Zeitraum ist der Kurs an drei Tagen jeweils um denselben Prozentsatz gestiegen, um 3,1 %. Das folgende Bild zeigt diese drei Punkte; die Ausschnitte stammen aus demselben linear skalierten Diagramm. Am 27./28. Mai (links) sieht die Steigung größer aus als dieselbe Steigung von 3,1 % am 29./30. Juli (Mitte). Und wiederum dieselben 3,1 % gehen vom 12. über das Wochenende zum 15. Dezember in der Darstellung vollkommen unter. Der Kurs stand bei 6,25 Euro im Mai, 4,93 Euro im Juli und 0,67 Euro im Dezember.

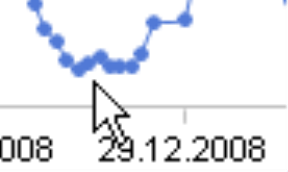Nun dieselben Ausschnitte in logarithmischer Skalierung:

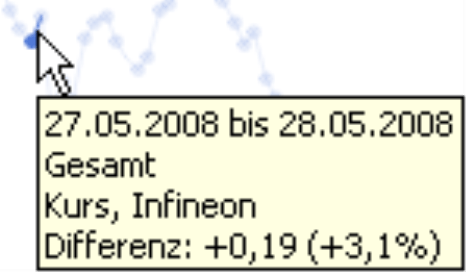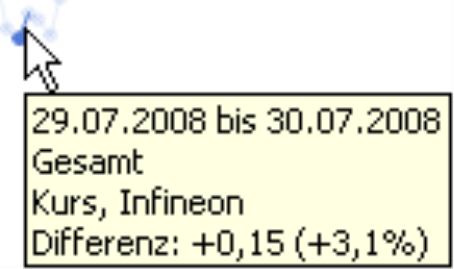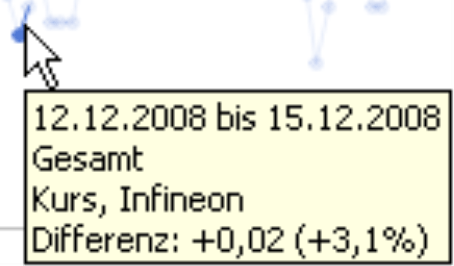Jetzt sehen alle Steigungen gleich aus. Erst die logarithmische Skala macht die relativen Veränderungen vergleichbar.

In der Totalen auf der nächsten Seite erkennt man, dass die Skalierung zu einem ganz anderen Bild der Lage führt.
Lineare Skala:

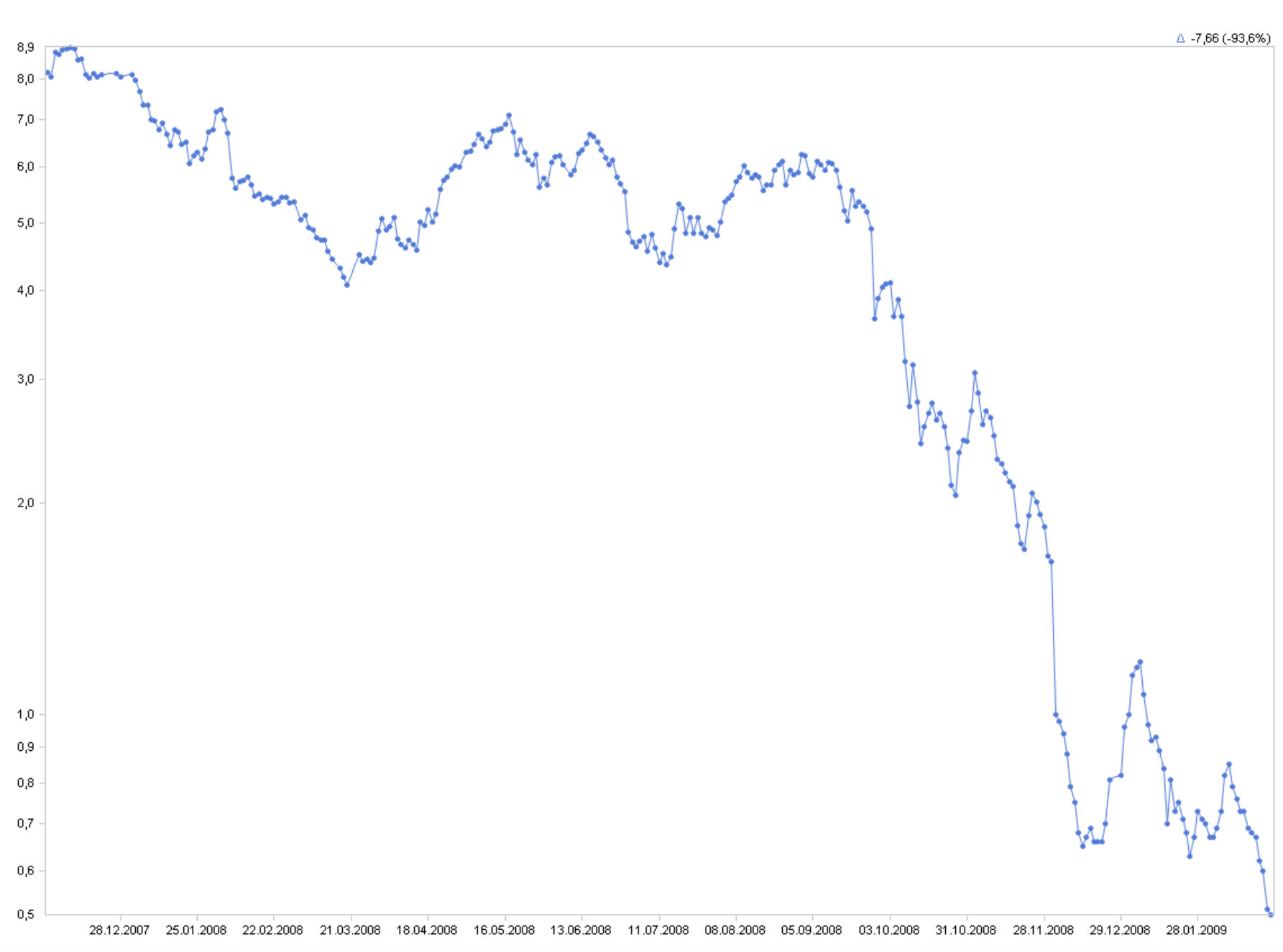
Logarithmische Skala:

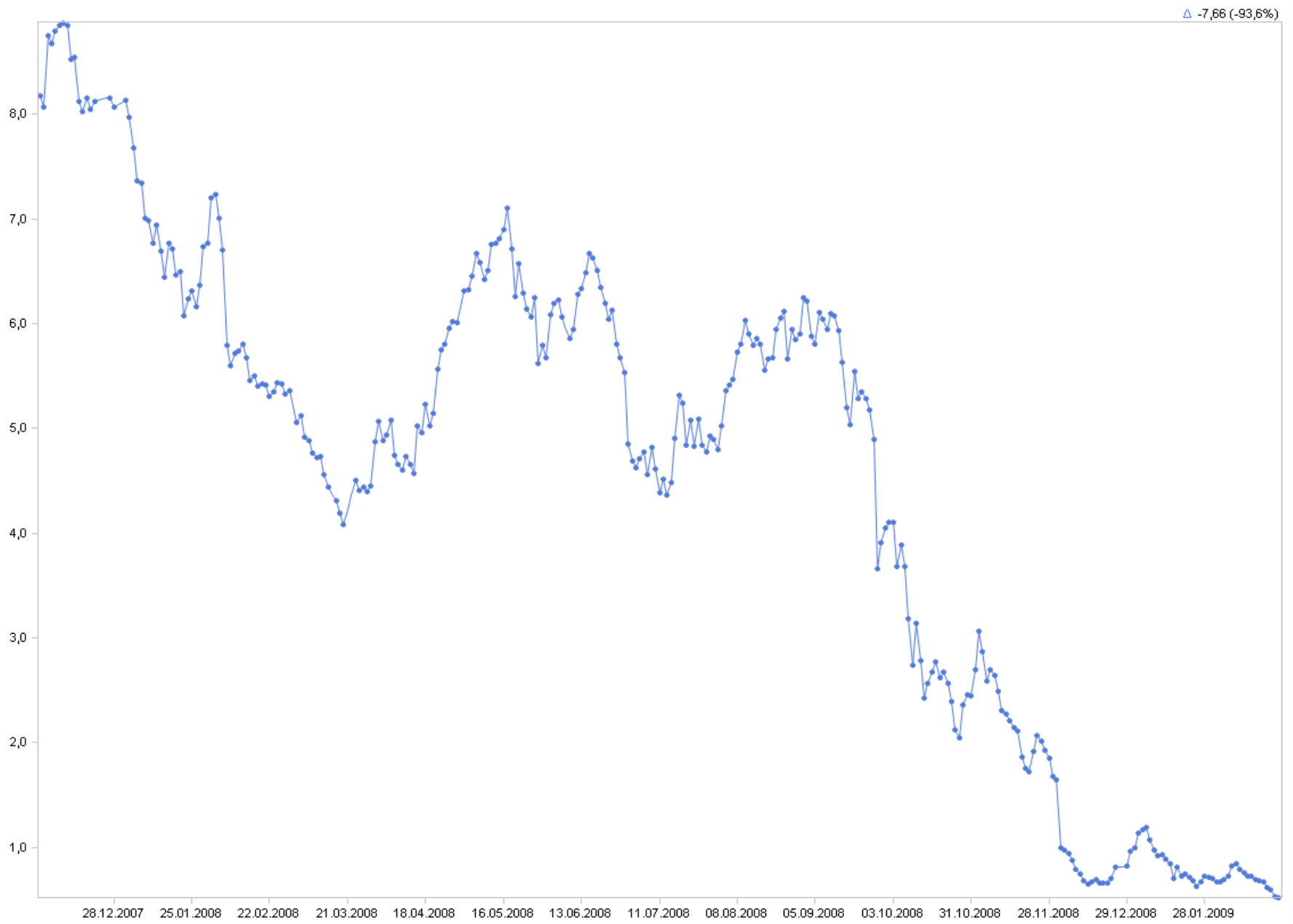
Beachten Sie vor allem die Ecke rechts unten: Bei linearer Skalierung meint man, die Aktie dümpele nur noch vor sich hin, mit lediglich einer kleinen Zuckung, die Anleger und Spekulanten kaum reizen dürfte. Bei logarithmischer Skalierung hingegen ist zu erkennen, dass in dieser Phase erhebliche relative Kursbewegungen stattfanden, auf niedrigem Niveau, aber mit Sprüngen von bis zu 17 %, was veritable Gewinne versprach.

Negativ ist anders, aber auch gleich

In realen Datenlagen, wie bei den Aktienkursen, findet man meist ein Auf und Ab der Werte, positive und negative Veränderungen in einem Diagramm. Kommt es darauf an, betragsgleiche positive und negative Veränderungen verzerrungsfrei darzustellen, versagen selbst logarithmische Skalen. Zwar wird eine Veränderung von +5 % im gesamten Diagramm stets als dieselbe Steigung dargestellt und ebenso wird eine Veränderung von –5 % im gesamten Diagramm stets als dieselbe Steigung dargestellt – diese ist aber nicht spiegelbildlich zu der Steigung von +5 %. In der Regel geht es uns jedoch um den Trendvergleich über mehrere Perioden, wo das eine untergeordnete Rolle spielt.

Frühwarnung dank logarithmischer Skalen

Vergleicht man noch einmal die beiden ersten Diagramme mit den fiktiven Zahlen, so fällt ein weiterer Vorteil der logarithmischen Achsenskalierung ins Auge: Sie erlaubt eine Frühwarnung.

Dass die Zuwächse prozentual gesehen abnehmen, kann man aus dem ersten Kurvenverlauf beim besten Willen nicht herauslesen, geht es doch mit konstanter Steigung bergauf. Kein Grund zur Sorge, signalisiert das. Beim zweiten, logarithmisch skalierten Graphen hingegen sieht jeder sofort: Noch wächst etwas, aber immer langsamer. Die Steigung nimmt ab. Eine fast verblüffende Erkenntnis: Diese einfache Form der Frühwarnung kommt ganz ohne komplizierte Prognose- und Simulationsalgorithmen aus. Es genügt, das entsprechende Diagramm richtig zu zeichnen, mit logarithmischer Skala nämlich.

Achsen abschneiden: bei Linien erlaubt und manchmal geboten

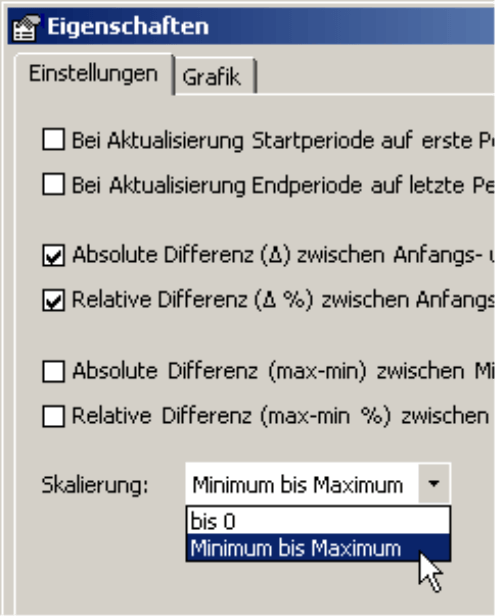
Entgegen einer weit verbreiteten Meinung ist es bei einem Liniendiagramm durchaus zulässig und in vielen Fällen sogar ratsam, die Y-Achse „abzuschneiden“, sodass nur der Bereich zu sehen ist, in dem sich die Werte bewegen, also zwischen dem Minimum und dem Maximum der Reihe. Das liegt an der Deutungspriorität: Bei einem Balken- oder Säulendiagramm achtet das Auge auf die Länge der Balken bzw. die Höhe der Säulen und somit den Abstand der Punkte zur Achse. Das Kürzen der Achsen führt zwangsläufig zu einer Verzerrung, weil die Wertunterschiede nicht mehr proportional zu den Längen-/Höhenunterschieden sind. Anders bei Liniensegmenten: Hier achten wir nicht auf den Abstand zur Achse, sondern primär auf die Steigungen der Liniensegmente. Das Auge gleitet förmlich von einem Punkt zum nächsten und streift über die Linie wie beim Blick über einen Bergkamm. Die Steigungen geben die Wertänderungen aber auch bei verkürzter Achse korrekt und unverzerrt wieder, eine logarithmische Skalierung vorausgesetzt. Deshalb sollte man die Achsen so definieren, dass die Veränderungen mit der größtmöglichen Differenzierung gezeigt werden.

Die Skalierung von Minimum bis Maximum ist in den Eigenschaften (Kontextmenü, Menü Ich möchte) der Zeitreihenanalyse direkt einstellbar. Damit kann man es sich ersparen, die Einstellungen für die Y-Achse (Kontextmenü der Achse in einem Zeitreihendiagramm) individuell zu bearbeiten; stattdessen wählt DeltaMaster den jeweils passenden Ausschnitt automatisch.

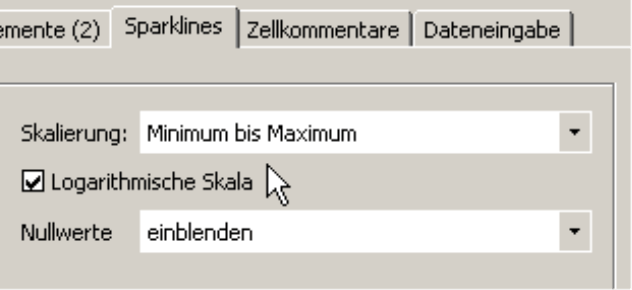
Logarithmisch skalierte Sparklines

Mit wenigen Mausklicks stellen Sie die logarithmische Skala auch für Sparklines in der Pivottabelle ein und passen gegebenenfalls die Skalierung so an, dass nur der Bereich zwischen Minimum und Maximum gezeichnet wird. Diese Optionen finden Sie in den Tabelleneigenschaften (Kontextmenü, Menü Ich möchte) der Pivottabelle auf der Registerkarte Sparklines.

Mathematischer Hintergrund für Nicht-Mathematiker

Zum Glück müssen wir nicht einsteigen in die Geheimnisse der Mathematik, wenn wir die logarithmische Skala verwenden wollen: Die Optionen, die es dazu braucht, sind in DeltaMaster leicht zu finden. Dennoch hat sich gezeigt: Manchen Anwendern erleichtert es das Verständnis, wenn sie die mathematischen Zusammenhänge kennen. Machen wir also einen kleinen Exkurs.

Der Logarithmus ist die Umkehrfunktion des Potenzierens. Zum Beispiel ist 10³ = 1.000; umgekehrt sagt man: „Der Logarithmus von 1.000 zur Basis 10 ist 3.“ Zur Basis 10 berechnet auch DeltaMaster den Logarithmus (dekadischer Logarithmus, „lg“), aber auch jede andere Basis würde eine maßstabsgetreue, unverzerrte Darstellung liefern. Für Null und negative Zahlen ist der Logarithmus nicht definiert. Für das Business Intelligence ist das schade, aber nicht zu ändern: Negative Zahlen in einer Datenreihe, wie sie etwa in Plan-Ist-Abweichungen vorkommen können, werden in einem Diagramm oder einer Sparkline nicht gezeichnet; die Reihe hat eine Lücke.

Eine wichtige Eigenschaft des Logarithmus ist: Man kann damit eine Multiplikation in eine Addition auflösen. Diese Qualität hat man sich beispielsweise bei Rechenschiebern zunutze gemacht und wenn wir Diagramme und Sparklines zeichnen, um relative Wertänderungen zu vergleichen, kommt sie uns ebenfalls zugute. Damit lässt sich zeigen, dass innerhalb einer Datenreihe tatsächlich gleiche relative Wertänderungen als gleiche Steigungen abgebildet werden:

• Eine relative Wertänderung kann man als eine Multiplikation verstehen. Ist beispielsweise der Umsatz von Mai auf Juni um 5 % gestiegen ist, so rechnen wir: „Umsatz_Juni = Umsatz_Mai * 1,05“. Um die entsprechende Grafik am Bildschirm aufzubauen, müssen wir ausrechnen, wo der Punkt für Juni zu zeichnen ist, das heißt, wie viele Pixel er höher liegt als der Punkt für den Startwert im Mai. Also ist eine Addition gefragt.
• Mathematiker wissen, dass dieser Zusammenhang gilt: log(a*b) = log(a) + log(b).
• Wenn wir bei „a“ an den Umsatz denken und bei „b“ an dessen Steigerungsrate, zum Beispiel 1,05 für eine Zunahme um 5 %, dann lautet der Ausdruck: „log(Umsatz * 1,05) = log(Umsatz) + log(1,05)“.
• Jetzt sieht man: „log(1,05)“ ergibt immer denselben Wert. Wenn also, wie im Beispiel, der Umsatz von Mai auf Juni um 5 % zunimmt, dann zeichnen wir den Juni-Wert immer um dieselbe Anzahl Pixel höher als den Mai-Wert – unabhängig davon, ob der Umsatz im Mai bei 10.000 oder bei 10 Millionen lag.

Wie sag ich’s dem Leser?

Im Wall Street Journal stößt man regelmäßig auf logarithmisch skalierte Diagramme für Börsenkurse. Als Erläuterung findet man etwa dies: „The charts show the percentage change in each index’s or stock’s value, rather than the point change, for purposes of comparison.“ Von Logarithmus kein Wort. Stattdessen weist man schlicht daraufhin, dass die Skala die Vergleichbarkeit der relativen Veränderungen herstellt. Vom üblichen Argument, logarithmische Darstellungen würden nicht verstanden, lässt sich das Journal also nicht von einer korrekten Darstellung abhalten. Das Wall Street Journal verkauft 2 Millionen Zeitungen täglich.

Manchmal nicht

Die logarithmische Skalierung bietet sich nur für Liniendiagramme an – für Säulen oder Balken ist sie ungeeignet: Wegen der Deutungspriorität würde die Logarithmierung bei diesem Diagrammtyp zu einer Verzerrung führen.

Wie oben beschrieben, ist der Logarithmus für negative Werte und für Null nicht definiert. Daher ist zu prüfen, wie groß die Lücken sind, die bei logarithmischer Skalierung entstünden. So könnte etwa die Visualisierung einer Abweichungskennzahl darunter leiden, wenn viele negative Werte nicht dargestellt werden können.

Die Verzerrung durch eine lineare Skala wird umso deutlicher, je stärker die Werte innerhalb der Reihe variieren. Sind hingegen in der gesamten Reihe nur geringe Änderungen zu verzeichnen, zum Beispiel weil sie einem nur sehr schwachen Trend folgt oder eng um einen Mittelwert pendelt, so sind die Verzerrungen zu vernachlässigen und es geht auch ohne logarithmische Skala.

Lesetipps

Für eine Renaissance der logarithmischen Skalierung machen wir uns schon seit langem stark. In diesen Blogartikeln finden Sie weitere Beispiele und Argumente:

• Vergleichen Zeitreihenvergleiche Zeitreihen?
• Müssen Manager den tollwütigen Logarithmus-Tiger reiten? (1)
• Müssen Manager den tollwütigen Logarithmus-Tiger reiten? (2)
• Unter Piratenflagge segeln
• Daten richtig darstellen: Deutungspriorität
• Über allen Gipfeln keine Ruh‘
• Verbieten verboten
  bzw. Regel 72: Schneide Linien ruhig die Füße ab
  im Buch „Bella berät“
• Log? Logo!
  bzw. Regel 73: Benutze logarithmische Skalen
  im Buch „Bella berät“