In Projekten stellt sich häufig die Frage, welcher Datentyp der richtige ist für die zugrunde liegenden Werte. Bei Dezimalzahlen hatte ich bisher float als Datentyp bevorzugt, bis ich jetzt aber auf die Probleme gestoßen bin, die diese Wahl mit sich bringt. In meinem konkreten Fall ist das Problem beim Runden einer berechneten Kennzahl im SQL-Server aufgetreten. Dieser Blogbeitrag zeigt das Ergebnis meiner Tests und Recherchen.
Innerhalb eines Projektes sind wir auf ein Phänomen gestoßen, das zunächst überraschend schien: ein berechneter Wert von exakt 1,5 sollte mittels SQL-Befehl ROUND gerundet werden. Zu erwarten wäre als Ergebnis den Wert 2, bekommen haben wir den Wert 1. Was ebenfalls zur Verwirrung beigetragen hat, war, dass die meisten Werte korrekt gerundet wurden, nur wenige Ausnahmen nicht. Die Ursache des Problems: der Datentyp der Werte innerhalb der Berechnung war float.
Über msdn.microsoft.com lässt sich schon der entscheidende Hinweis finden: float sowie real sind „ungefähre Zahlendatentypen“ und hierfür gilt folgende Definition: „Ungefähre Zahlendatentypen für numerische Gleitkommadaten. Gleitkommadaten sind Näherungswerte, deshalb können nicht alle Werte im Bereich des Datentyps exakt dargestellt werden.“ (Quelle: https://msdn.microsoft.com/de-de/library/ms173773.aspx)
Korrektes Runden
In diesem konkreten Fall trat das Problem beim Runden eines Wertes auf, der vorher aus drei Kennzahlen errechnet werden musste. Nachzustellen ist die Problematik recht einfach:
DECLARE @f float
SET @f = 2.3
SELECT
(@f - 2) * 5 AS value,
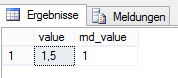
ROUND((@f - 2) * 5, 0) AS rnd_valueWird @f als 2,3 definiert, lautet die Berechnung (2,3 -2)*5, mit 1,5 als Ergebnis. Gerundet auf ganze Zahlen sollte sich hier der Wert 2 ergeben, im SQL-Server wurde allerdings 1 ausgewiesen.
Abbildung 1: Rundungsergebnis der Berechnung mit float
Auch der Wert @f = 3,3 wird falsch gerundet, @f = 4,3 aber wiederum korrekt, hier wird das Ergebnis von 11,5 richtig auf 12 gerundet.
Auch bei weniger Berechnungsschritten, wie z. B. direkt 0,3*5 wird wieder richtig auf 2 gerundet.
DECLARE @f float
SET @f = 0.3
SELECT
@f * 5 AS value,
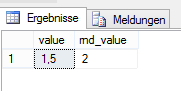
ROUND(@f * 5, 0) AS rnd_valueAbbildung 2: Rundungsergebnis der Berechnung mit weniger Berechnungsschritten mit float
Innerhalb meiner Berechnungskette gibt es also einen Zwischenschritt, der mit dem Datentyp float nicht in jedem Fall exakt wiedergegeben wird.
Um das Problem zu lösen, setze ich im ersten Beispiel den Datentyp von float auf numeric. So wird das Ergebnis immer korrekt gerundet.
DDECLARE @f numeric(10,1)
SET @f = 2.3
SELECT
(@f - 2) * 5 AS value,
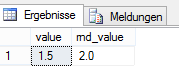
ROUND((@f - 2) * 5, 0) AS rnd_valueAbbildung 3: Rundungsergebnis der Berechnung mit numeric
Aggregation
Ein weiteres Problem beschreibt folgender Beitrag:
http://holgerschmeling.blogspot.de/2009/12/aggregatfunktionen-und-der-datentyp.html
In diesem Blogbeitrag wird dargestellt, dass die Summierung über Werte vom Datentyp float zusätzlich nicht reproduzierbar ist. Vor allem bei einer größeren Anzahl an Datensätzen lassen sich eindeutige Schwankungen feststellen. Und: Je größer die einzelnen Datenwerte, desto höher die absolute Auswirkung.
Wir haben das Skript aus diesem Blogbeitrag mit deutlich mehr Datensätzen (zwei Millionen) nachgestellt. Allerdings mit einer kleineren, für gängige Projekte realistischeren Zahl.
In einer Testtabelle wird ein Wert x-fach eingefügt, einmal mit positivem Vorzeichen und dieselbe An-zahl Datensätze mit negativen Vorzeichen, so dass die Summe über die Spalte immer 0 ergeben sollte. Getestet wird in einer Spalte mit dem Datentyp float, in einer zweiten Spalte mit Datentyp decimal(38,5). Der Tabellenaufbau für die Testtabelle ist wie folgt definiert:
-- Testtabelle anlegen
CREATE TABLE Test_float
(c1 float
,c2 decimal(38,5))
GO
DECLARE @x decimal(38,5)
SET @x = 1000.12345
-- Werte in die Testtabelle eintragen
INSERT Test_float(c1,c2)
SELECT @x, -@x
FROM ( SELECT ROW_NUMBER() OVER (ORDER BY current_timestamp) as rn
FROM sys.trace_event_bindings as a
,sys.trace_event_bindings as b) as rd
WHERE rn <= 1000000
-- Noch einmal dieselben Werte, diesmal mit umgekehrten Vorzeichen
INSERT Test_float(c1,c2)
SELECT -@x, @x
FROM ( SELECT ROW_NUMBER() OVER (ORDER BY current_timestamp) as rn
FROM sys.trace_event_bindings as a
,sys.trace_event_bindings as b) as rd
WHERE rn <= 1000000
GOIm Anschluss habe ich noch einmal überprüft, ob tatsächlich exakt die gleichen Werte in jeder Spalte zu finden sind:
-- Testabfrage, sind wirklich dieselben Werte in jeder Spalte?
SELECT c1
,c2
,count(*) Anzahl_DS
FROM Test_float
GROUP BY c1
,c2
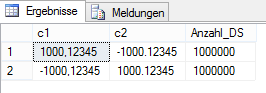
GOAbbildung 4: Test des Tabelleninhalts
Schließlich folgt die Abfrage der Spaltensummen: zehnmal dasselbe SELECT-Statement untereinander. Erwartungsgemäß sollte die Summe in jeder Spalte immer genau 0 ergeben, oder, unter der Prämisse, dass float nicht exakt ist, zumindest immer denselben Wert in der Nähe von 0.
-- Summenbildung über float und decimal
SELECT SUM(c1) AS SumFloat, SUM(c2) AS SumDecimal FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
UNION ALL
SELECT SUM(c1), SUM(c2) FROM Test_float
GODas Ergebnis der Abfrage variiert allerdings von Durchlauf zu Durchlauf, hier ein Beispiel eines möglichen Ergebnisses:
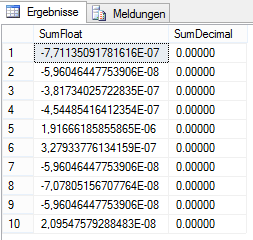
Abbildung 5: Ergebnis der Aggregation von float im Vergleich zu decimal
Die Summe der float-Spalte ergibt niemals exakt 0, bei Summierung von zwei Millionen Datensätzen mit einem Wert von ca. 1.000 liegt die Differenz aber erst in der 6. bis 8. Nachkommastelle. Bei höheren Werten ist die absolute Abweichung von 0 entsprechend größer.
Hier wird auch ersichtlich, dass neben der Problematik der nur ungefähren float-Zahlenwerte auch die Summenbildung in sich nicht konsistent ist. Fast jede Ausführung ergibt eine leicht abweichende Summe. Die Erklärung hierfür liefert der Ausführungsplan.
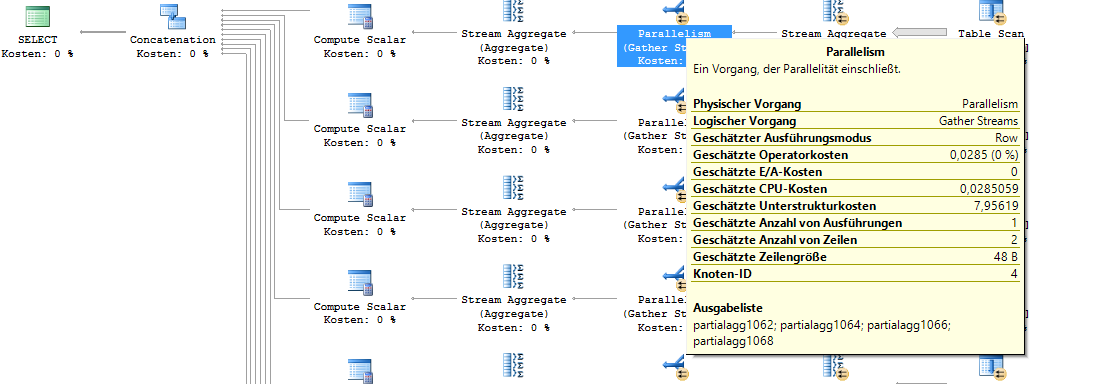
Abbildung 6: Ausschnitt aus dem Ausführungsplan der Aggregation
Die Aggregation der Werte erfolgt parallel über, in diesem Fall, vier Threads (siehe „Ausgabeliste“ im Screenshot). Jedes einzelne Select-Statement der Abfrage wird über vier verschiedene partielle Aggregationen erstellt, die hinterher zusammengeführt werden. Der Zeitpunkt der Zusammensetzung der Threads hängt bei jeder Ausführung von der aktuellen Auslastung der CPU ab, und kann somit minimal variieren. Da die Threads somit nicht in jedem Fall exakt übereinstimmen, werden hier letztendlich in jeder Ausführung vier verschiedene aggregierte Werte zusammengeführt, jeder für sich „ungefähr“. Das führt auch wieder zu „ungefähren“ und somit variablen Endergebnissen.
Eine Lösung für die Aggregationsproblematik kann unter Umständen sein, die parallele Ausführung zu verhindern und die Berechnung über nur einen Thread zu erzwingen über den Befehl
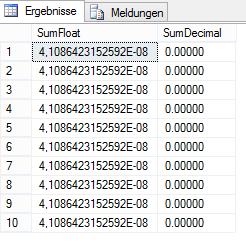
Mit dieser Bedingung ausgeführt, erhöht sich einerseits die Abfragezeit deutlich und das Ergebnis aus obigem SELECT-Statement ist auch immer noch nur näherungsweise 0. Aber zumindest ergibt sich derselbe Wert bei jedem Ausführen des Statements, da hier der Zwischenschritt über die erneute Zusammenführung der ungefähren Werte aus mehreren Threads entfällt.
Abbildung 7: Ergebnis der Aggregation von float im Vergleich zu decimal mit nur einem Thread
Interessehalber habe ich die Testtabelle auch einmal mit sehr viel kleineren Werten gefüllt und teilwei-se auch mit nur sehr geringen Datenmengen. Hier ein Auszug der Ergebnisse:
- @x = 1.5, rn = 1000000
- @x = 2.5, rn = 1000000
⇒ Ergebnis in beiden Fällen: SumFloat = 0 bei jeder Ausführung
- @x = 2.3, rn = 100000
- @x = 2.8, rn = 100000
⇒ Ergebnis in beiden Fällen: Abweichung ab der 8. Nachkommastelle
- @x = 2.3, rn = 1000
- @x = 2.8, rn = 1000
⇒ Ergebnis in beiden Fällen: Abweichung in der 13. Nachkommastelle
- @x = 2.3, rn = 100
- @x = 2.8, rn = 100
⇒ Ergebnis in beiden Fällen: Abweichung in der 14. Nachkommastelle
Werte wie 1,5 und 2,5 scheinen also tatsächlich exakt gespeichert zu sein, die Beispielwerte 2,3 und 2,8 hingegen nicht.
Fazit
Zusammengefasst ist der Datentyp float unter gewissen Voraussetzungen mit Vorsicht zu behandeln. Bei Aggregation von großen Datenmengen kann es zu Abweichungen im Bereich von Nachkommastellen kommen. Bei Berechnungen mit float-Kennzahlen, vor allem wenn das Ergebnis gerundet dar-gestellt werden soll, kann es ebenfalls zu Ungenauigkeiten kommen. In solchen Fällen sollte besser ein Datentyp wie decimal oder numeric verwendet werden.
Kleiner Exkurs
Decimal und numeric werden im SQL-Server gleich behandelt. Beides sind exakte Datentypen. Der einzige Unterschied: numeric wird in genau der angegebenen Präzision gespeichert, decimal in mindestens der angegebenen Präzision. Verwendet werden können beide synonym. (Quelle: https://docs.microsoft.com/en-us/sql/t-sql/data-types/decimal-and-numeric-transact-sql)
Der Datentyp money kann gegebenenfalls auch eingesetzt werden, ist aber nur bis zur vierten Nachkommastelle exakt und kann somit unter Umständen auch zu Problemen führen.
Der Vorteil von float liegt allerdings in dem vergleichsweise geringeren Speicherplatz gegenüber decimal oder numeric-Datentypen. Float benötigt 8 bytes im Standard, decimal und numeric je nach Genauigkeit bis zu 17 bytes. Die Frage die sich also immer stellt: Was möchte ich mit meiner Kennzahl machen und reicht dafür ein „ungefährer“ Datentyp?