Logarithmische Skalen gelten manchen als tollwütige Tiger*. Ohne sie ist aber jede zweite Grafik falsch skaliert. Eine kleine Serie zeigt, wie wir den Tiger bändigen und uns in der nächsten PowerPoint-Präsentation entspannt zurücklehnen, wenn über Skalen schwadroniert wird.
Der Beitrag über die Tücken der Zeitreihenanalyse bewegt die Gemüter. Ich hatte festgestellt, dass die meisten Zeitreihenvergleiche sinnlos sind, weil sie nicht zeigen, was sie zeigen sollen. Ein Vergleich der Preisentwicklung für Heizöl, Strom und Gas aus der Welt am Sonntag diente dabei als Beispiel. Sie verstößt gegen Bellas ehernes Proportionalitätsgesetz. Es besagt: Grafische Veränderungen müssen proportional zu den abgebildeten Wertveränderungen sein. Der Verstoß der Grafik gegen Bellas Dogma ist erheblich.
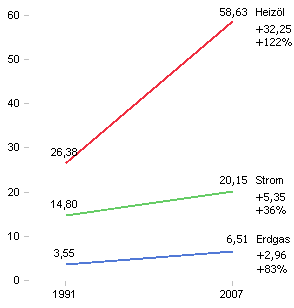
Absolut steigt Heizöl um 58,63 – 26,38 = 32,25 Einheiten. Erdgas steigt um 6,51 – 3,55 = 2,96 Einheiten. Grafisch steigt Heizöl damit um den Faktor 32,25 / 2,96 = 11 stärker als Erdgas.
Prozentual steigt Heizöl um 122 %, Erdgas um 83 %. Damit steigt Heizöl also nur um den Faktor 122/83=1,5 stärker.
Die Grafik untertreibt den Anstieg von Erdgas um den Faktor 11/1,5=7,33.
Wie erheblich, das können wir mit dem Lügenfaktor messen, mit dem wir Excels Diagrammassistenten bereits einen Teil des Untergangs der abendländischen Datenkultur in die Zellen schieben konnten. Der Diagrammassistent lügt notorisch. Er schneidet Säulen und Balken automatisch ab. Die resultierenden Unterschiede zwischen den Säulen und Balken haben mit den Wertunterschieden, die sie abbilden sollten, nur noch wenig Ähnlichkeit. Wir messen, wie lang einer der verzerrten Balken ist und wie lang er sein sollte, teilen das eine durch das andere und bekommen ein Maß für die Unter- oder Übertreibung.
Bei Liniengrafiken können wir dieses Prinzip auf die abgebildeten Steigungen übertragen. In der Energiepreisgrafik ist je nach Blickrichtung die Steigung des Heizöls um das Siebenfache über- bzw. die Steigung des Erdgases um das Siebenfache untertrieben.
Warum ist das so? Eine Liniengrafik zeigt Wertänderungen zwischen zwei Perioden durch die Steigung der sie verbindenden Linie. Wir haben gelernt, je steiler die Linie, desto größer die Steigung und eben die Wertänderung. In der Energiepreisgrafik kommen wir damit aber ins Schleudern: Heizöl steigt steiler als Erdgas und Strom. Halt! Ist das wirklich so? Wir sehen näher hin: Nur wenn wir die absoluten Werte betrachten. Aber können wir denn absolute Wertänderungen betrachten, wenn wir von unterschiedlichen Niveaus starten? Natürlich nicht. Die Steigungen sind offensichtlich nicht proportional zu den prozentualen Preisänderungen. Ja, was sagen denn dann die Steigungen aus?
Wir sehen: Steigungen müssen für prozentuale Wertänderungen reserviert bleiben. Anderenfalls verstoßen wir gegen Bellas Proportionalitätsgesetz. Im besten Fall werden wir nur schlecht verstanden, im schlimmsten Fall wirft man uns Manipulation vor.
Erste Alternative zum Tigerritt: Normierung
Eine erste Lösung des Problems ist die Normierung der Werte auf einen einheitlichen Startwert. Man teilt alle Werte einer Reihe durch den Anfangswert der Reihe. Der erste Wert jeder Reihe ist damit 100 und alle anderen Werte sind in Bezug zu diesem Startwert gesetzt. Eine praktikable Lösung, wenn die Unterschiede am Anfang keine Rolle spielen.
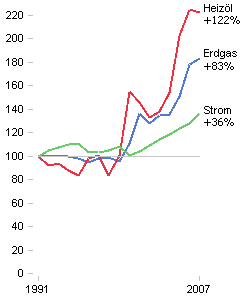
Zeitungen schrecken vor Normierungen im allgemeinen zurück. Man kann sich das Dilemma vorstellen, in dem ein Redakteur steckt. Jede Umformung muss vom Leser verstanden werden. Gezeigt werden nicht mehr die tatsächlichen Werte. Es wird deutlich, wie wichtig und gleichzeitig willkürlich die Wahl des Startpunktes ist. Die Darstellung der Istwerte wirkt demgegenüber unverfänglicher.
Dennoch: Wer Grafiken produziert, die Strom steiler als Erdgas steigen lassen, obwohl Strom nicht einmal halb so stark wie Erdgas stieg, der braucht dringend eine Alternative.
* Logarithmische Skalen – Tagesgespräch zu Börse und Wirtschaft – GoldSeiten-Forum.de
