Liebe Datenanalysten,

Überblick und Detail: Auf beides kommt es an in der Managementinformation – und besonders auf einen flüssigen Wechsel zwischen beidem. Das erleben Sie regelmäßig in vielen interaktiven Darstellungen und in den Analyseverfahren von DeltaMaster. Zu diesen gehört auch die Verteilungsanalyse, ein statistisches Verfahren zur Untersuchung von Häufigkeiten. Sie liefert mehr Details als eine Spitzenkennzahl wie der Monatsumsatz und mehr Überblick als etwa eine Auflistung sämtlicher Kunden- oder Produktumsätze. Dazu wird der Umsatz (oder ein anderer Analysewert) in eine überschaubare Anzahl von Intervallen eingeteilt. Dann zählt man, wie viele Kunden oder Produkte (oder andere Objekte) jeweils in diese Intervalle fallen. Das Ergebnis ist als übersichtliches Histogramm oder als Tabelle leicht zu interpretieren und zu präsentieren. Wissenswertes über die Verteilungsanalyse haben wir in diesen clicks! für Sie zusammengestellt – im Überblick und im Detail.

Herzliche Grüße
Ihr Team von Bissantz & Company

Wer Daten intensiv analysiert, benötigt immer wieder einmal einen Überblick über die Häufigkeitsverteilung der Untersuchungsobjekte: der Kunden, Produkte, Materialien, Relationen, Wirtschaftseinheiten usw. Dafür empfiehlt sich die Verteilungsanalyse von DeltaMaster. Sie zeigt, wie oft die interessierenden Objekte in verschiedenen, aufeinanderfolgenden Intervallen auftreten, und berechnet statistische Maße, die die Verteilung der Werte beschreiben, zum Beispiel Mittelwert, Median und Spannweite.

Manche Anwender schätzen besonders die grafische Darstellung als Histogramm, andere den schnellen Zugriff auf die Kenngrößen. Außerdem können die Objekte wertabhängig in Klassen eingeteilt werden, die sich wiederum als Filter für andere Analysen verwenden lassen, zum Beispiel: Kunden mit einem Umsatz unter 20.000, zwischen 20.000 und 40.000, zwischen 40.000 und 60.000 usw.

Erstellt werden Verteilungsanalysen im Modus Miner-Expert, abrufen kann man sie natürlich auch in den Modi Reader, Viewer, Pivotizer und Analyzer und natürlich im neuen DeltaMaster Navigator. Im Folgenden zeigen wir, wie Sie die Analyse einrichten, wie das Histogramm zu lesen ist, was die statistischen Maße bedeuten und wie Sie die Analyseergebnisse als virtuelle Hierarchie weiterverwenden.

Los geht‘s

Die Verteilungsanalyse ist im Analysemenü unter den statistischen Verfahren eingeordnet. Sie benötigt nur zwei Parameter: eine Dimensionsebene und einen Analysewert. Als Beispiel aus unserer Referenzanwendung „Chair“ dienen uns die Kunden (unterste Ebene der Kundendimension) und der Umsatz – wir wollen wissen, in welchen Umsatzklassen die Kunden rangieren.

• Die Dimensionsebene wählen Sie mit dem Menü oberhalb der Grafik (bzw. des dafür vorgesehenen Rahmens) aus. Berücksichtigt werden alle Elemente dieser Ebene, die zur aktuellen Auswahl im Fenster Sicht und gegebenenfalls zu den Filtern in den Einstellungen passen. Mit der Sicht und den Filtern können Sie also die Menge der zu analysierenden Objekte einschränken. Die Sicht kann im Modus Viewer geändert werden, die Filter nicht.
• Den Analysewert wählen Sie mit dem Menü unterhalb der Grafik. Alternativ können Sie ihn per Drag-and-drop aus einem Cockpit übernehmen.

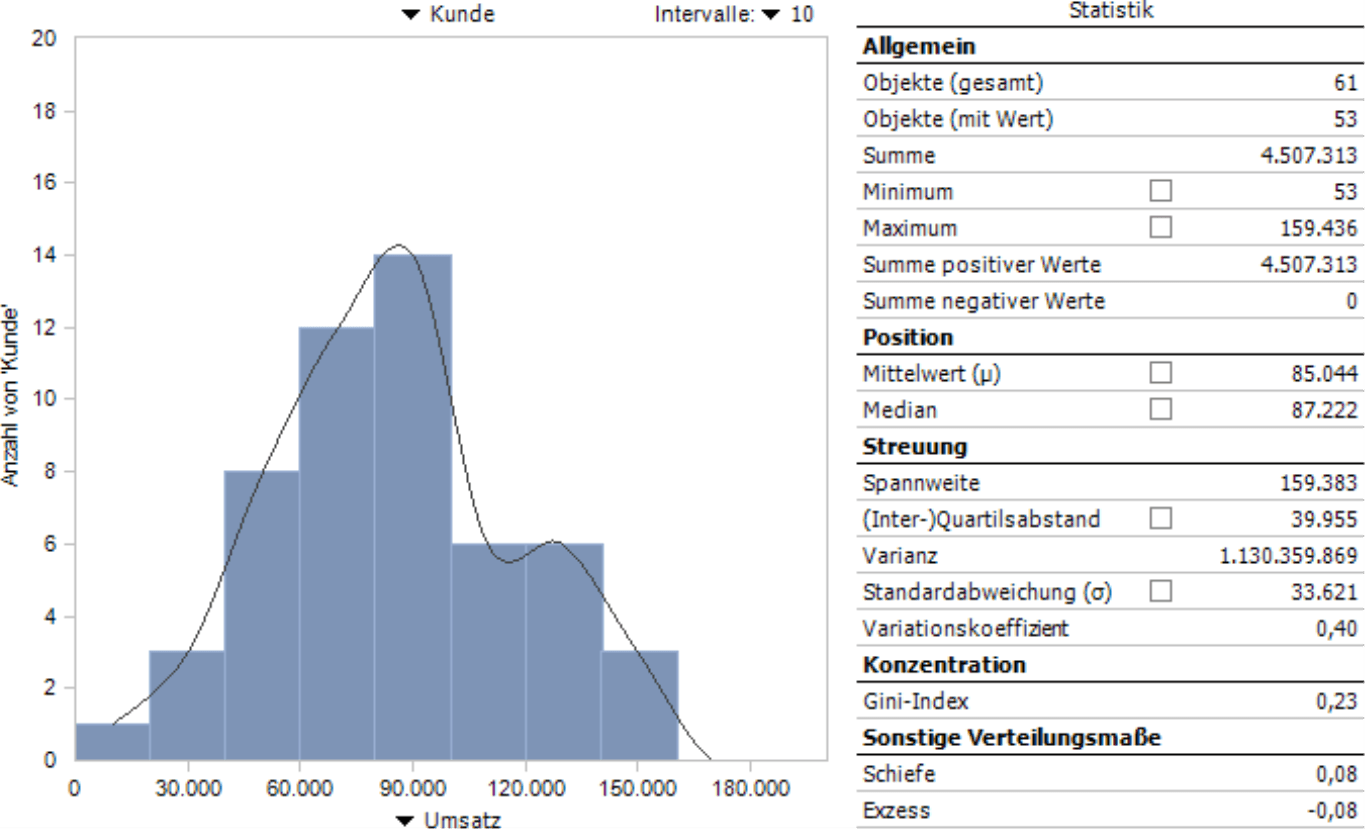
Wenn Sie die Analyse berechnen lassen, zeichnet DeltaMaster die Verteilung der Objekte als Histogramm und gibt eine Tabelle mit statistischen Maßen zu dieser Verteilung aus, wie in der vorigen Abbildung. Falls die Darstellung unter Ausreißern leidet, können Sie diese durch Filter (Menü im Fenster Analyse) eliminieren.

Werfen wir zunächst einen genaueren Blick auf das Histogramm; die Statistik erläutern wir weiter unten.

Histogramm

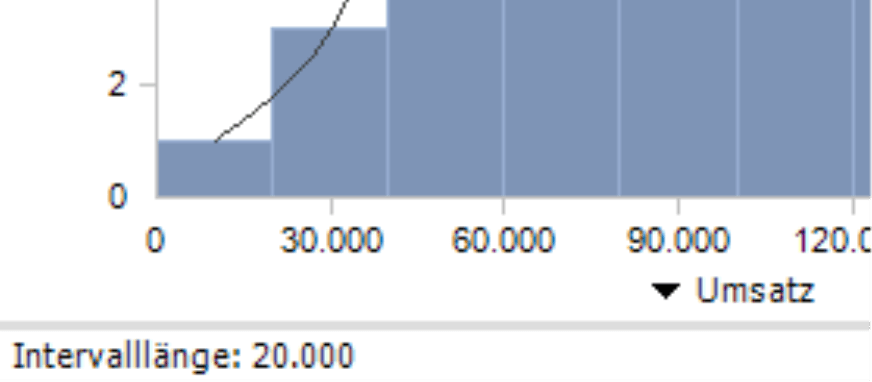
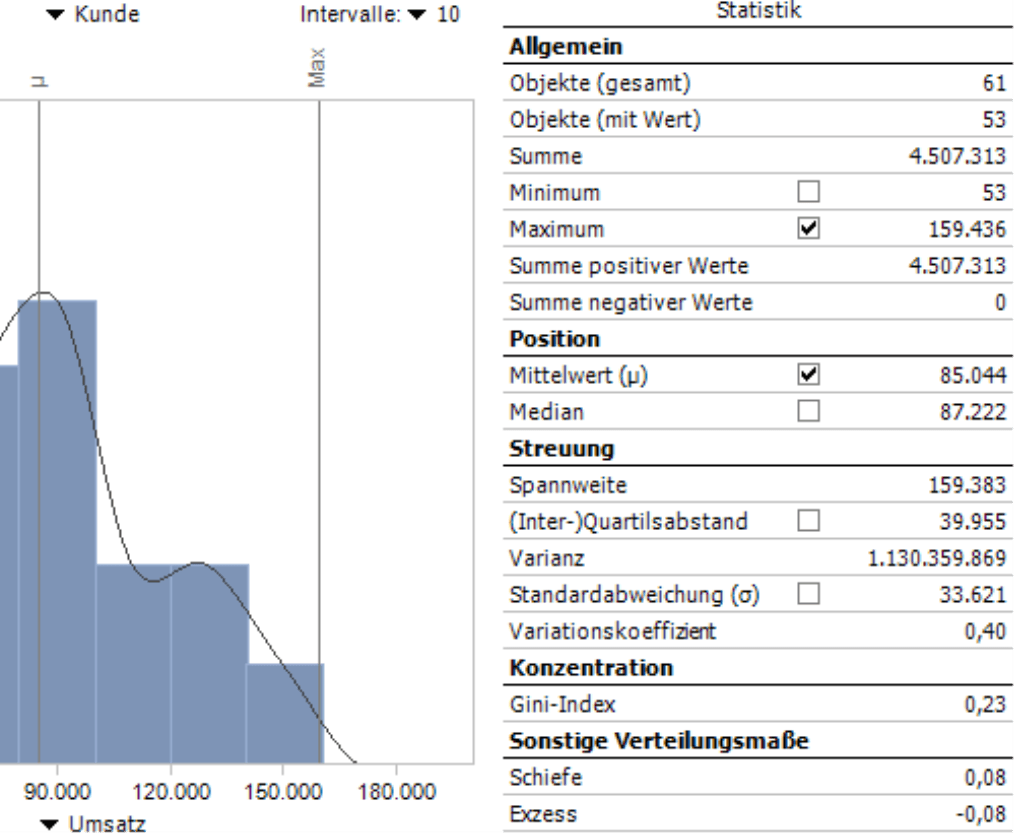
Auf der Abszisse (X-Achse) ist der Analysewert abgetragen, hier: der Umsatz. Dabei wurden automatisch Intervalle gebildet. Diese Intervalle sind ein Wesensmerkmal der Verteilungsanalyse: Man unterteilt den Wertebereich in zusammenhängende Teilbereiche und untersucht, wie viele Elemente in welchen Teilbereich fallen. Die Intervalle sind gleich breit. Ihre Anzahl (und damit auch ihre Breite) lässt sich in der Auswahlliste rechts oberhalb der Grafik einstellen. Wie viele Intervalle es sein sollen, lässt sich nicht verallgemeinern. Mit einer größeren Anzahl wird die Darstellung feiner, man läuft aber Gefahr, dass die Essenz der Verteilung inmitten von mehr oder weniger zufälligen Ausprägungen nicht mehr zu erkennen ist. Eine kleinere Anzahl reduziert den Einfluss von „Lücken“ und Ausreißern, führt aber zu einer groben Darstellung und möglicherweise zu einer wenig sensiblen Zusammenfassung von Objekten. Häufig ist die Struktur der Verteilung mit fünf bis zwanzig Intervallen ganz gut zu erkennen; im Zweifel probieren Sie aber auch andere Werte aus.

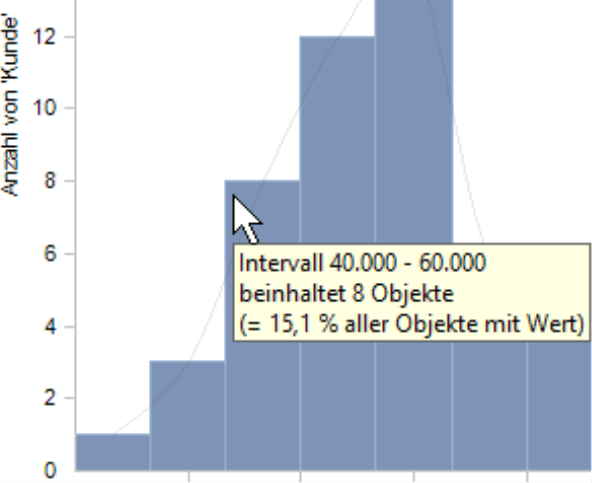
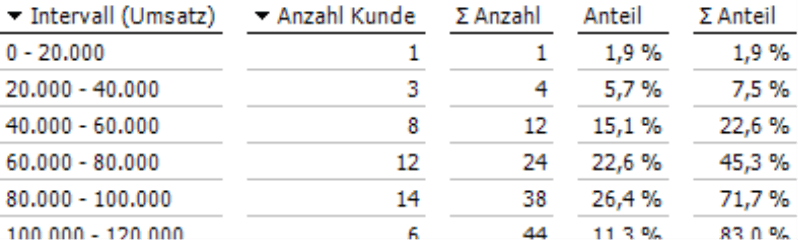
Auf der Ordinaten (Y-Achse) wird die Anzahl der Objekte abgetragen, hier also: wie viele Kunden in der jeweiligen Umsatzklasse liegen. Im Tooltip der Säulen sind die Grenzen des Intervalls sowie die Anzahl der zugehörigen Elemente angegeben, letztere einmal absolut und einmal als Anteil an allen Elementen, die einen Wert haben (siehe unten den Hinweis zur Anzahl der Objekte im Abschnitt Allgemein).

In der tabellarischen Ansicht (Menü im Fenster Analyse bzw. Bericht) sind die gleichen Angaben enthalten: die Intervallgrenzen, die Anzahl der Elemente in einem Intervall und welchen Anteil diese ausmachen. Zusätzlich werden Anzahl und Anteil in den Spalten mit dem Summen-Symbol in der Überschrift von oben nach unten aufaddiert. Damit ist eine kumulative Betrachtung ähnlich der ABC-Analyse möglich: Wie viele Objekte liegen in den ersten zwei, drei, vier, … Klassen zusammen und welchen Anteil haben sie zusammen?

Statistik

Rechts neben dem Histogramm sind statistische Maßzahlen angegeben, die die Verteilung charakterisieren. Einige davon lassen sich im Histogramm anzeigen, indem Sie das entsprechende Kontrollkästchen aktivieren.

Allgemein

Die allgemeinen Angaben sind kaum erklärungsbedürftig. Sie beschreiben den Umfang der Datenbasis und den Wertebereich.

Position

Um eine Reihe von Werten zu beschreiben, nimmt man häufig einem „mittleren“ Wert als Anhaltspunkt.

Falls der verwendete Analysewert nicht additiv ist (zum Beispiel bei einer prozentualen Abweichung oder einem Quotienten wie einem Marktanteil oder einer Rabattquote), berechnet DeltaMaster den Mittelwert und den Median ungewichtet, das heißt, ohne Kenntnis der absoluten Basisgrößen. Liegt beispielsweise die Rabattquote für Kunden im Inland bei 4 Prozent, für Kunden im Ausland bei 8 Prozent, so ergibt sich als Mittelwert 6 Prozent, unabhängig davon, wie hoch die Umsätze und Rabatte im Inland und im Ausland sind. Daher sind Mittelwert und Median „mit Vorsicht zu genießen“. Auf diesen Umstand weist DeltaMaster ausdrücklich hin: Die statistischen Angaben werden kursiv geschrieben und in der Statusleiste des Berichts ist vermerkt, dass diese Werte ungewichtet sind. Als nicht additiv gilt ein Analysewert, wenn in seinen Analysewerteigenschaften auf der Registerkarte Allgemein die Additivität so eingestellt ist.

Streuung

Mit Streuungsmaßen drückt man aus, wie dicht die Werte der betrachteten Verteilung um einen Mittelwert liegen.

Spannweite	Differenz von Maximum und Minimum; sozusagen der „Abstand“ zwischen kleinstem und größtem Wert. Die Spannweite ist das einfachste Maß für die Variabilität einer Verteilung.
(Inter-)Quartilsabstand	Differenz zwischen oberem und unterem Quartil. Wie beim Median denkt man sich die Werte in einer aufsteigend sortierten Liste. Der Quartilsabstand ist dann die „Spannweite der mittleren Hälfte“ (der mittleren 25 bis 75 Prozent). Das Viertel mit den kleinsten Werten und das mit den größten wird für diese Maßzahl nicht beachtet. Das begrenzt den Einfluss von Ausreißern.
Varianz	Durchschnittliche quadratische Abweichung vom Mittelwert. Durch das Quadrieren ist die Varianz betriebswirtschaftlich kaum zu interpretieren und oft verblüffend groß, aber sie ist für weiterführende Berechnungen von Bedeutung.
Standardabweichung (?)	Durchschnittliche Streuung um den Mittelwert; berechnet als Wurzel aus der Varianz. Die Standardabweichung wird oft angewendet, um Klassen mit den häufigsten Merkmalen zu bilden. Voraussetzung ist, dass die Analysewerte einer Normalverteilung unterliegen (Glockenkurve ). Dann gilt: Im Bereich vom Mittelwert plus/minus einer Standardabweichung liegen rund 68 Prozent aller Werte, in einem Bereich vom Mittelwert plus/minus zwei Standardabweichungen liegen rund 95 Prozent aller Werte. Auch für Prognosezwecke eignet sich die Standardabweichung: Ein niedriger Wert lässt auf eine hohe Wahrscheinlichkeit schließen, dass auch zukünftige Ergebnisse nahe dem Durchschnitt liegen.
Variationskoeffizient	Relatives Streuungsmaß; berechnet als Quotient aus Standardabweichung und Mittelwert. Auf dieser Basis können die Standardabweichungen von Verteilungen vergleichbar gemacht werden, auch wenn sie sich absolut stark unterscheiden, zum Beispiel bei Umsätzen des Konzerns und der Tochtergesellschaften.

Falls der verwendete Analysewert nicht additiv ist, gelten für die Varianz, die Standardabweichung und den Variationskoeffizienten die gleichen Hinweise wie für den Mittelwert und den Median: Die Berechnung ist ungewichtet, siehe oben.

Konzentration

Zwei extreme Verteilungen sind die Gleichverteilung einerseits und die Verteilung auf einen Punkt andererseits. Wie die zu untersuchende Verteilung in diesem Spektrum einzuordnen ist, beschreibt man mit Konzentrationsmaßen.

Sonstige Verteilungsmaße

Analysekettentechnik: Klassen oder Intervalle als virtuelle Hierarchie verwenden

Eine Besonderheit der Verteilungsanalyse von DeltaMaster ist, dass man die analysierten Elemente – die Kunden, Produkte usw. – neu zusammenfassen und als virtuelle Hierarchie für weitere Analysen mit DeltaMaster zur Verfügung stellen kann. Die Zusammenfassung und die Hierarchiebildung orientieren sich wahlweise an den Intervallen oder an Klassen, die den Wertebereich zusätzlich einteilen.

Klassen sind besonders dann praktisch, wenn man eine größere Anzahl von Intervallen konfiguriert hat, die nicht alle zu Elementen der virtuellen Hierarchie werden sollen, oder wenn die Klassengrenzen explizit bzw. abweichend von Intervallgrenzen festgelegt werden sollen. Als Voreinstellung richtet DeltaMaster in jeder Verteilungsanalyse automatisch vier Klassengrenzen mit gleichen Abständen ein.

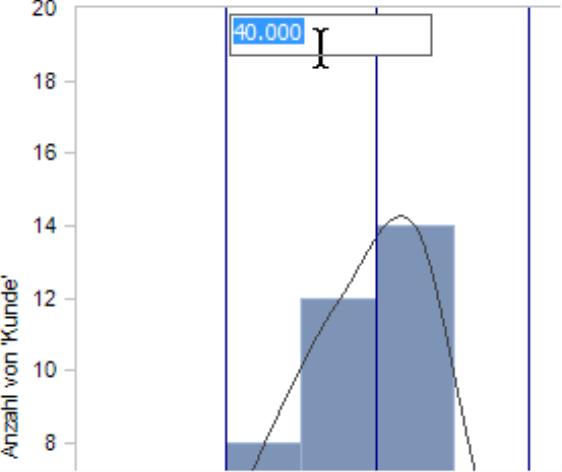
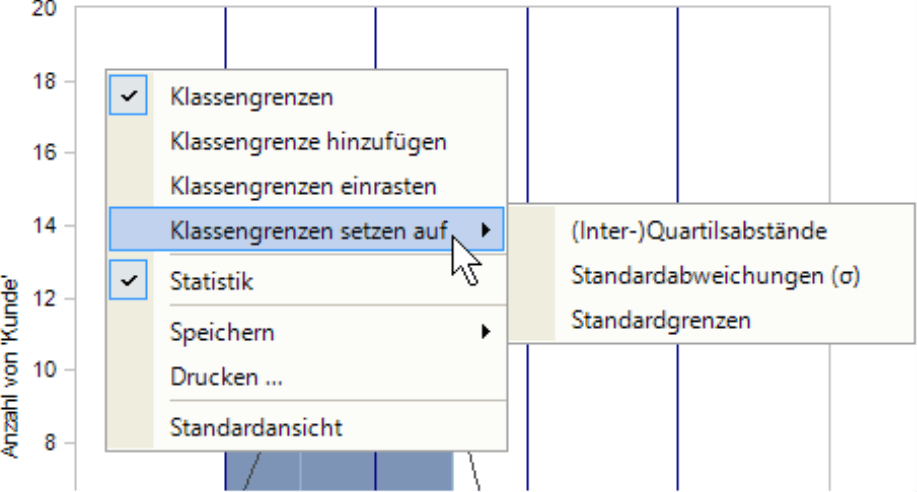
Die Klassen sind im Histogramm an vertikalen Linien zu erkennen, sobald Sie die Klassengrenzen einblenden (Menü Ich möchte oder Kontextmenü der Grafik). Per Drag-and-drop können die Grenzen verschoben werden. Über das Kontextmenü einer Linie können Sie zudem numerisch eine Klassengrenze setzen und den gewünschten Wert exakt eingeben. Dazu erscheint neben der Linie ein kleines Eingabefeld. Das Feld ist mit der bisherigen Einstellung vorbelegt. Prozentzahlen geben Sie einschließlich des Prozentzeichens ein.

Über das Kontextmenü des Diagramms lassen sich weitere Klassengrenzen hinzufügen. Das Einrasten bewirkt, dass Klassengrenzen, die durch ein Intervall verlaufen, an eine Intervallgrenze verschoben werden. Als schnelle Voreinstellung lassen sich die Klassengrenzen auf oft verwendete Grenzwerte setzen: die (Inter-)Quartilsabstände (Erläuterung siehe oben im Abschnitt Statistik/Streuung), der Mittelwert plus/ minus ein und zwei Standardabweichungen oder die vier Standardgrenzen von DeltaMaster. Alle drei Optionen setzen eine vorherige Klasseneinteilung zurück (sie werden also nicht zusätzlich zu individuellen Klassen eingerichtet). Die Grenzen nach der Standardabweichung zu setzen, bewährt sich häufig, um Ausreißer in den Griff zu bekommen: Bei normalverteilten Werten liegen 95 Prozent der Werte innerhalb des Bereichs von zwei Standardabweichungen um den Mittelwert, die übrigen kann man meist als Ausreißer betrachten und ignorieren.

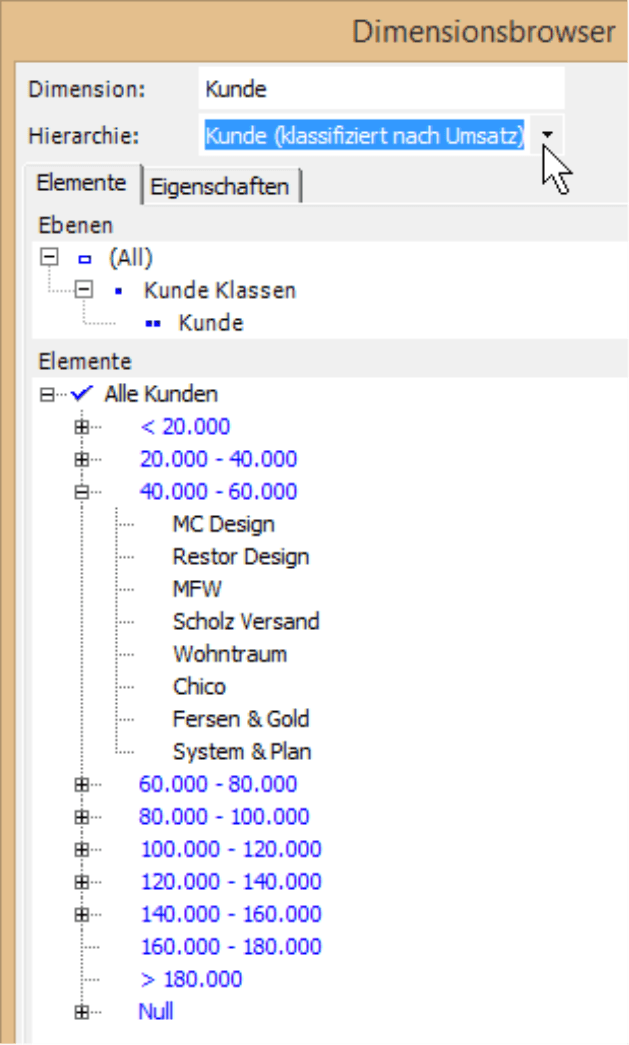
Sind die Intervalle oder Klassen eingestellt, erzeugen Sie eine virtuelle Hierarchie mit den Funktionen im Menü Drill-in, wahlweise mit den Klassen oder den Intervallen. Falls Sie speziell an einem bestimmten Intervall interessiert sind, geht es noch schneller: Mit einem Doppelklick auf die entsprechende Säule erstellt DeltaMaster eine virtuelle Hierarchie gemäß den Intervallen und wählt im Fenster Sicht automatisch das angeklickte Intervall aus.

Die neue Hierarchie steht unmittelbar in DeltaMaster zur Verfügung, ohne Änderungen an der Datenbank. Im abgebildeten Dimensionsbrowser ist die neue Gliederung deutlich zu erkennen: Die Kunden sind jetzt nicht mehr regional gegliedert, sondern nach Umsatzklassen. Diese Klassen lassen sich als Ausgangspunkt für weitere Analysen verwenden.

Zur Einordnung der Elemente in die virtuelle Hierarchie verwendet DeltaMaster MDX-Ausdrücke. Diese bestimmen die Klassenzugehörigkeit anhand des Analysewerts, der Sicht und der Filter, wie bei der Berechnung der Analyse eingestellt. Die virtuelle Hierarchie ist also nicht über statische Aufzählungen definiert, sondern über dynamische Beschreibungen, sodass spätere Änderungen in der Datenbank automatisch berücksichtigt werden. In den Einstellungen (Menü im Fenster Analyse) auf der Registerkarte Klassifikation lässt sich steuern, wo DeltaMaster die Nullwerte, also Elemente ohne Wert, unterbringen soll: in einer regulären Klasse (die auch die Elemente mit einem Wert von 0 aufnimmt) oder in einer zusätzlichen Klasse, die eigens für die „leeren“ Elemente angelegt wird. Elemente, die durch Filter in den Einstellungen ausgesondert wurden, fasst DeltaMaster automatisch in einer eigenen Klasse zusammen.

Wurde für die aktuelle Ansicht der Verteilungsanalyse bereits eine virtuelle Hierarchie erzeugt, so kann keine weitere gespeichert werden und die Funktionen zum Bearbeiten von Klassengrenzen sind deaktiviert. In der Statusleiste wird ein Hinweis ausgegeben, dass bereits eine virtuelle Hierarchie erstellt ist. Um weitere virtuelle Hierarchien zu erzeugen, berechnen Sie die Analyse neu.

Weitere Analysen mit den statistischen Maßen

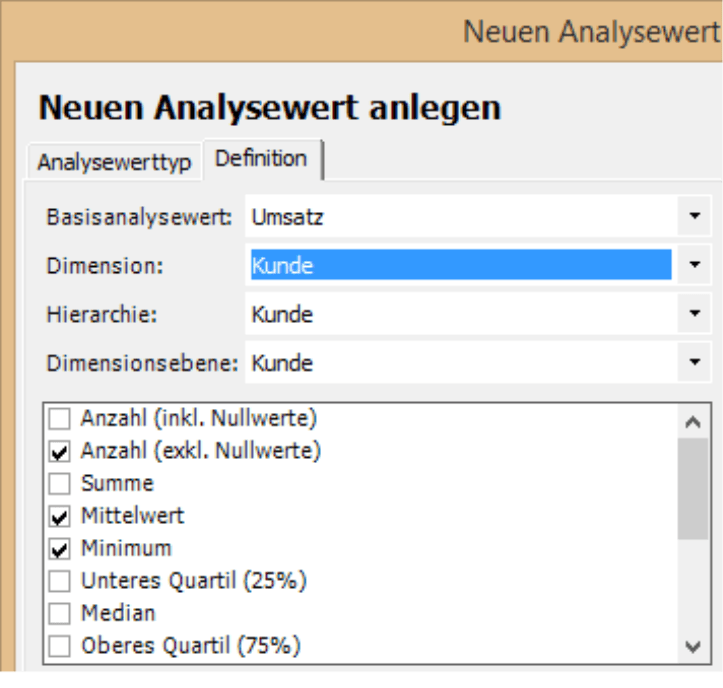
Nicht nur die Intervalle und Klassen, sondern auch die im Feld Statistik angegebenen Kenngrößen lassen sich weiterverwenden. In einer Pivottabelle beispielsweise könnte man diese Maße vergleichen, ihre zeitliche Entwicklung mit Sparklines verfolgen oder sie schlicht als zusätzliche Information in umfangreiche Berichte integrieren. Eine direkte Übernahme aus der Verteilungsanalyse ist nicht möglich – jedoch können fast alle oben vorgestellten statistischen Maße mühelos als eigenständige Analysewerte definiert werden. Dazu legt man mithilfe des Assistenten im Analysewert-Browser (Menü Modell) univariate statistische Analysewerte an. Lediglich der (Inter?) Quartilsabstand, der Gini-Index, die Schiefe und der Exzess stehen dort nicht zur Verfügung (siehe DeltaMaster clicks! 07/2009).

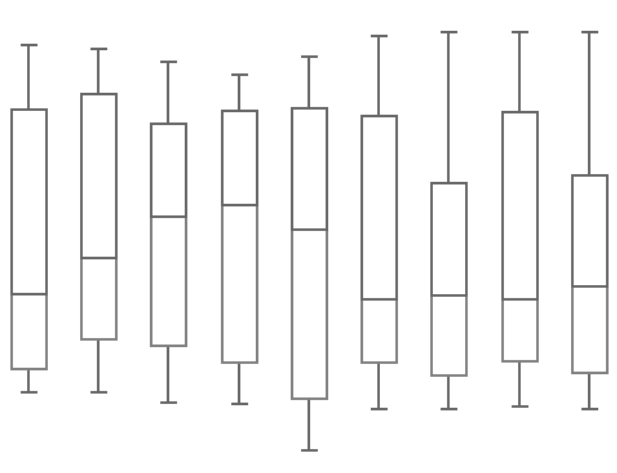
Alternativen: Box-Whisker-Diagramme und Boxplots in Grafischen Tabellen

Zum Vergleichen von Verteilungen bietet DeltaMaster außerdem die Darstellung als Box-Whisker-Diagramm bzw. als Boxplot an. Beide visualisieren Lage und Streuung von Werten mithilfe von fünf univariaten statistischen Analysewerten: dem Minimum, dem unteren Quartil, dem Median, dem oberen Quartil und dem Maximum. Bei einem Box-Whisker-Diagramm handelt es sich um eine Pivotgrafik, bei Boxplots um grafische Elemente, die in Pivottabellen eingebettet sind.

Box-Whisker-Diagramme haben wir ausführlich in den DeltaMaster clicks! 12/2010 vorgestellt.

Die in Pivottabellen eingebetteten Boxplots liegen horizontal. Anstelle der „Antennen“, die im Diagramm Minimum und Maximum markieren, sind die Boxen von einem Rahmen umschlossen. Die Darstellung ist besonders einfach zu lesen und lässt sich sehr gut automatisch erstellen und aktualisieren. In den DeltaMaster deltas! 5.5.9, Punkt 11, ist beschrieben, wie Sie Boxplots einrichten und interpretieren und was dabei zu beachten ist.