Liebe Datenanalysten,

noch vor einigen Jahren waren statistische Verteilungen zwar nicht in aller Munde, aber doch in aller Hände: Die Zehn-Mark-Scheine der vierten und letzten Serie zierten das Portrait von Carl Friedrich Gauß und, links daneben, eine Normalverteilungskurve, die er erfunden hatte. Der Schein ist Geschichte, aber sich mit der statistischen Verteilung von Kennzahlen zu beschäftigen, lohnt sich nach wie vor: Über Standardberichte mit verdichteten Kennzahlen hinaus wollen wir manchmal auch die Verteilung und Streuung beurteilen können. Sind Durchlaufzeiten stabil oder schwanken sie in größeren Bereichen? Konnten wir Ausreißer in den Fehlerraten eindämmen? Sind die Lieferzeiten nicht nur im Mittel in Ordnung, sondern streuen auch wenig? Verhalten sich Absatzmärkte homogen? Für solche anspruchsvollen Fragestellungen ist es mit einem einfachen Durchschnitt nicht immer getan. Um Verteilungen zu beschreiben und zu erklären, greifen Statistiker gerne auf sogenannte Box-Plots zurück. In DeltaMaster sind sie schnell erzeugt und mit den Erläuterungen in diesen clicks! auch schnell verstanden. Vielleicht halten sie ja demnächst auch in Ihr Reporting Einzug und werden dann, zum Beispiel mit dem Berichtsserver, ganz normal verteilt.

Herzliche Grüße
Ihr Team von Bissantz & Company

Controlling und Statistik haben mal mehr, mal weniger miteinander zu tun. Mehr vor allem dann, wenn wir uns von einem standardisierten Listenreporting lösen und zur Analyse übergehen. Eine sortierte Liste von Kundenumsätzen beispielsweise hat sicher ihre Berechtigung – aber Erkenntnisse über die Verteilung der Umsätze oder gar Verschiebungen in der Verteilung, die im Zeitablauf aufgetreten sind, lassen sich damit nur schwer gewinnen. Auf den folgenden Seiten möchten wir Ihnen eine Darstellungsform näherbringen, die es bei einigen DeltaMaster-Anwendern bereits in Standardberichte und ?Cockpits geschafft hat: die sogenannten Box-Plots. Mit ihnen untersucht man eine größere Menge von Werten hinsichtlich ihrer Verteilung oder ihrer Streuung. Sicher sind auch Ihnen solche Diagramme schon einmal begegnet.

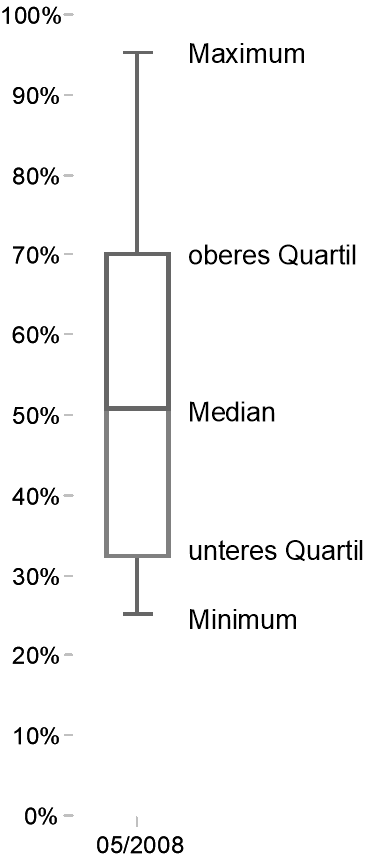
Die Box-Plots visualisieren die Lage und Streuung von Werten in einer Verteilung (einer Stichprobe). Im Unterschied zu manch anderen Diagrammtypen werden nicht einzelne Objekte (Kunden, Produkte, Fertigungsaufträge, Sendungen, Servicefälle usw.) gezeichnet. Vielmehr stützt sich die Darstellung auf fünf statistische Maße, die die Verteilung als Ganzes charakterisieren: das Minimum, das untere Quartil, der Median, das obere Quartil und das Maximum. (Auf die statistischen Hintergründe kommen wir noch zu sprechen.)

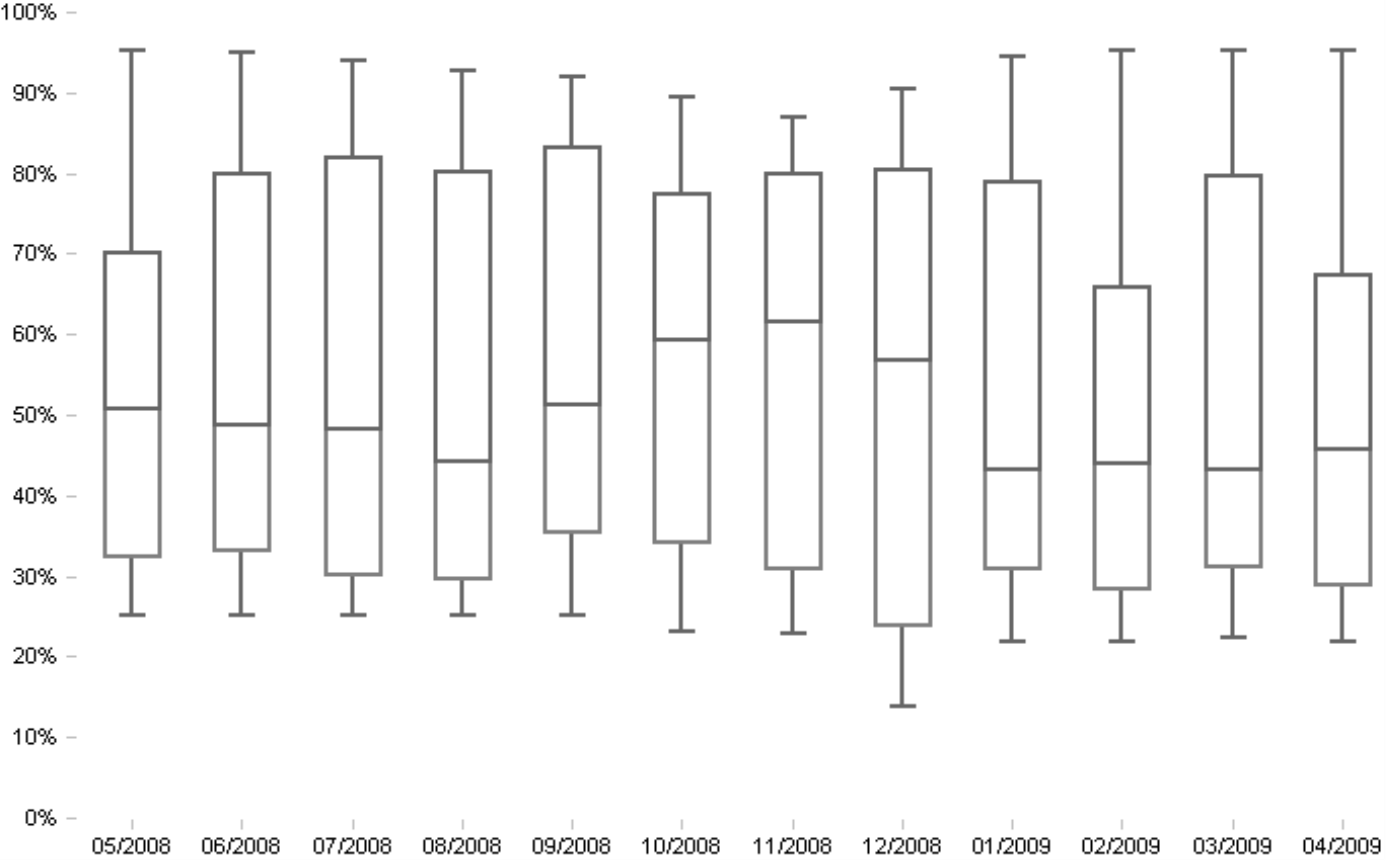
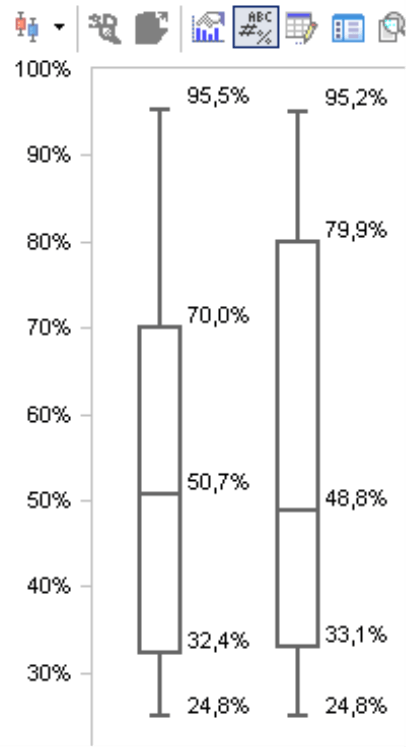
In der Abbildung sind die Deckungsbeitragsquoten von Produkten dargestellt. Man kann jeden Plot für sich betrachten oder die Entwicklung der Verteilungen über die Zeit verfolgen. Zu erkennen ist: Die Spannweite hat sich kaum verändert, der Median ist aber zwischen August und November gestiegen. Das bedeutet, dass sich mehr Produkte mit einer höheren Marge verkaufen ließen. Im Januar hingegen sanken einige Produkte wieder auf eine niedrigere Marge ab. Den Produktmanager sollte das warnen, vielleicht laufen Kosten aus dem Ruder oder Preise lassen sich nicht wie bisher durchsetzen.

Wie man Box-Plots erstellt, zeigen wir weiter unten an unserer Referenzanwendung „Chair“, also an Finanz- und Vertriebskennzahlen. Mit Box-Plots untersucht man aber auch andere Unternehmensbereiche:

• Im Produktionscontrolling kann man beispielsweise Durchlaufzeiten, Fehlerraten, Wartungsintervalle oder Pufferbestände untersuchen. Haben Änderungen von Prozessparametern dazu geführt, dass der Prozess „stabiler“ wird? Das könnte man etwa daran ablesen, dass die entsprechenden Produktionskennzahlen weniger streuen und die Extremwerte im Zeitablauf näher an den Kasten bzw. den Zentralwert rücken. Und wie hat sich dieser bewegt? Ist „im Mittel“ (zur Definition des Mittels siehe unten) eine Verbesserung oder Verschlechterung festzustellen? Wie stark streuen die Messungen um das Mittel?

• Ähnliche Fragen entstehen im Logistikcontrolling, wenn wir beispielsweise nach Lieferzeiten oder Verfügbarkeiten fragen. Hinter solchen Vorgängen stecken oft erhebliche Kosten, die durch mangelnde oder schlecht genutzte Kapazitäten entstehen.

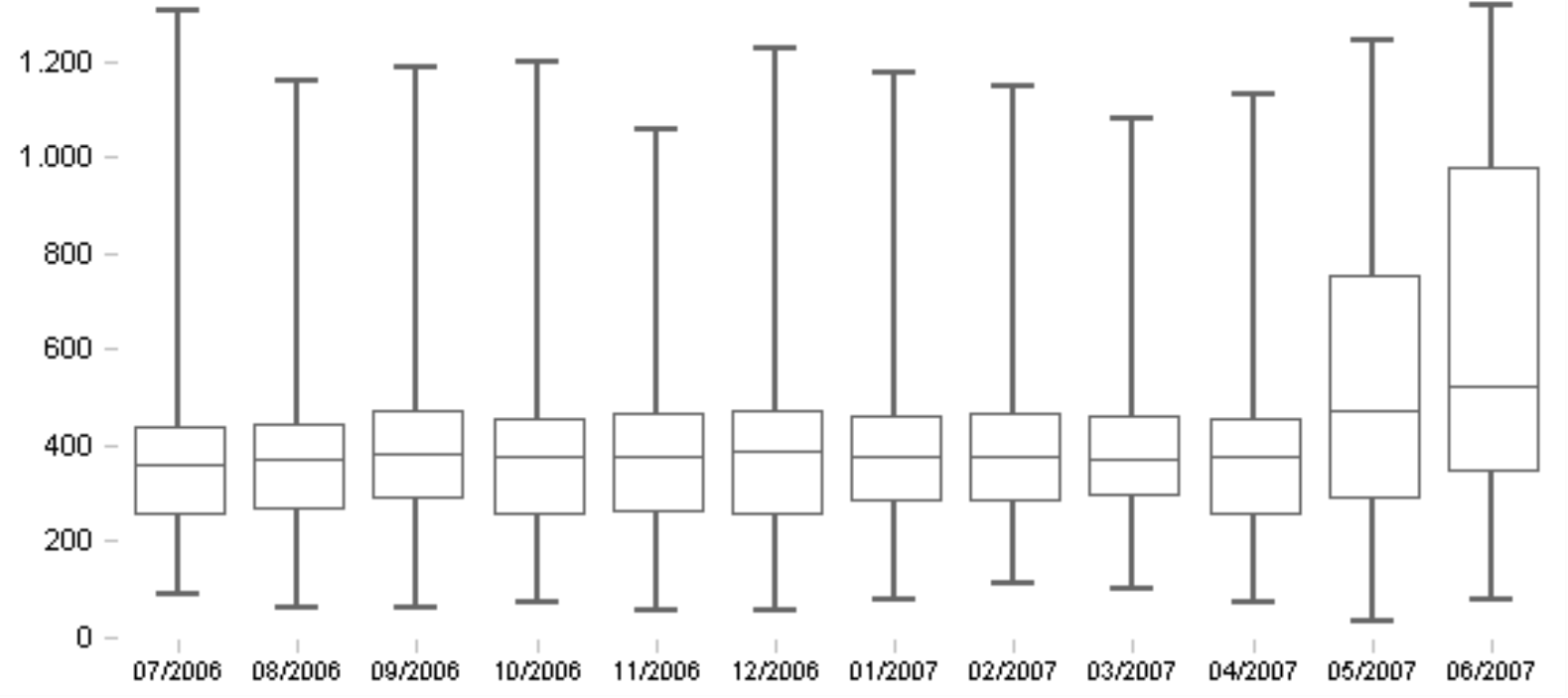
Das obige Beispiel stammt aus einer Anwendung zum Transportcontrolling, untersucht wird die Kennzahl „Leistungskosten pro Container nach Kunden“. Wir sehen, dass die Kostenverteilung über mehrere Monate hinweg recht konstant war: Der Median bewegte sich nicht viel, der Kasten mit den mittleren 50 Prozent der Werte ändert sich weder in seiner Lage noch in seiner Größe nennenswert – die Dinge nahmen ihren „geregelten Lauf“. Im Juni jedoch sind die Kosten pro Transportmittel bei den Kunden höher und vor allem sehr unterschiedlich ausgefallen, was weitere Nachforschungen anstoßen wird. Die Veränderung zeichnete sich schon im Mai ab.

• Im Vertrieb, um wieder zu diesem Beispiel überzuleiten, mag man sich fragen, wie homogen sich verschiedene Marktsegmente verhalten, was nicht nur in der Natur der jeweiligen Segmente liegen muss, sondern auch Hinweise auf eine mehr oder weniger effektive Führung der Segmente geben kann, abzulesen an einer höheren Gleichmäßigkeit und geringeren Bandbreite.

Aufbau von Box-Plots

Box-Plots werden auch Box-Whisker-Plots genannt. Offensichtlich ist mit der Box der Kasten in der Mitte gemeint, als Whisker bezeichnet man die „Antennen“ nach oben und unten. Die deutsche Bezeichnung Kastengrafik ist nach unserer Beobachtung wenig verbreitet.

Die erwähnten fünf statistischen Kenngrößen sind im Bild leicht zu erkennen: Die obere/untere Kante des Kastens steht für das obere/untere Quartil. Die Linie in der Mitte des Kastens zeigt die Lage des Medians. Die Enden der beiden Linien mit ihren Querstrichen markieren das Maximum bzw. das Minimum. Für die Interpretation der Darstellung sind die Abstände zwischen den fünf Markierungen wichtig, die Breite des Kastens hingegen ist ohne Bedeutung. Dass an der Y-Achse Prozentwerte stehen, liegt nicht am Verfahren, sondern daran, dass der betrachtete Analysewert, die Deckungsbeitragsquote, eine Prozentzahl ist. Die Einheiten der Kennzahlen bleiben im Box-Plot erhalten, andere Daten würden also in Euro, Stück, Minuten usw. ausgegeben.

Median und Quartile, was war das noch …

In die Tiefen der deskriptiven Statistik wollen wir hier nicht abtauchen, aber eine kleine Auffrischung der Grundlagen kann nicht schaden – denn auch wenn Box-Plots in DeltaMaster einfach zu erstellen sind, so benötigt man zur Interpretation und Reaktion auf Rückfragen mitunter doch etwas mehr Hintergrundwissen als für einfache Säulen oder Balken in Diagrammen und Grafischen Tabellen.

• Der Median, auch Zentralwert genannt, liegt in einer sortierten Wertreihe in der Mitte: Die Hälfte der Werte ist größer als er (oder gleich groß), die andere Hälfte ist kleiner als er (oder gleich groß). Wenn wir beispielsweise die Werte 10, 20, 30, 40 und 1.000 betrachten, ist der Median 30. Der Median ergibt sich nicht wie das arithmetische Mittel durch Addieren und Dividieren, sondern gewissermaßen durch „Abzählen“: Man wandert gedanklich so lange von den kleinen zu den großen Werten, bis man die Stelle gefunden hat, an der sich die Reihe in zwei mengenmäßig gleichgroße Abschnitte teilen lässt. In vielen Situationen ist der Median aussagekräftiger als das arithmetische Mittel, weil er unempfindlicher gegenüber Ausreißern ist. So auch in der genannten Reihe: Deren Mittelwert von 220 beschreibt die vier kleinen Werte ebenso wie den Extremwert von 1.000 nur schlecht – der eine Ausreißer hat das arithmetische Mittel auf einen Wert gehoben, der mit keiner der Messungen viel zu tun hat. Der Median hingegen repräsentiert die ihn umgebenden Werte ganz gut und lässt den Ausreißer als ebensolchen erscheinen.

• Quartile, auch Viertelwerte genannt, folgen dem gleichen Prinzip. Auch sie sind Werte, die eine sortierte Reihe teilen, nur nicht in der Mitte, sondern an ihrem unteren und oberen Viertel. Das untere Quartil (25-Prozent-Quartil) ist demnach ein Wert, der größer ist als ein Viertel der Werte und kleiner als die übrigen drei Viertel. Das obere Quartil (75-Prozent-Quartil) ist ein Wert, der größer ist als drei Viertel der Werte und kleiner als das übrige Viertel. In diesem Sinne kann der Median auch als mittleres Quartil oder als 50-Prozent-Quartil beschrieben werden.

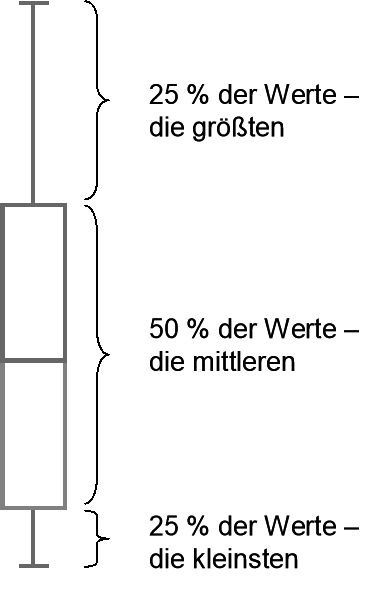
Mit diesen pragmatischen Erklärungen können wir festhalten: Die mittleren 50 Prozent der Werte liegen zwischen dem unteren und dem oberen Quartil (siehe Abbildung auf der nächsten Seite). Dieser Bereich wird im Box-Plot als Kasten gezeichnet. Innerhalb des Kastens markiert eine Linie den Median. Da es sich nicht um den Durchschnitt handelt, muss er nicht in der Mitte des Kastens liegen; vielmehr spiegeln Kasten und Medianmarkierung wider, wie sich die mittleren 50 Prozent der Werte um den Zentralwert verteilen. Die 25 Prozent der kleinsten Werte liegen zwischen dem Minimum und dem unteren Quartil. Das entspricht dem Bereich zwischen dem Ende der unteren „Antenne“ und dem unteren Ende des Kastens. Die 25 Prozent der größten Werte liegen zwischen dem oberen Quartil und dem Maximum. Das entspricht dem Bereich zwischen dem oberen Ende des Kastens und dem Ende der oberen „Antenne“.

Wie die Werte rechnerisch ermittelt werden, ist eine Wissenschaft für sich. Beispielsweise kommt es darauf an, ob die Anzahl der Werte ungerade, gerade oder durch vier teilbar ist. Die Programmiersprache „R“ unterscheidet geschlagene neun Varianten, Quantile zu berechnen. Für unsere Zwecke brauchen wir es nicht auf die Spitze zu treiben: Mit eventuellen Rundungsungenauigkeiten und Nuancen in den Definitionen können wir leben, wenn unsere Wertreihe groß genug ist. Das dürfte regelmäßig ab ungefähr 30 Werten der Fall sein – eine vergleichsweise kleine Zahl, angesichts der Datenmengen, mit denen wir es in Controllinganwendungen zu tun haben. Ein nachkommastellengenauer Ausweis der Verteilungskennzahlen ist für die Managementinformation nicht entscheidend; vielmehr kommt es darauf an, dass wir die Verteilung optisch erfassen und beurteilen und mit anderen Verteilungen vergleichen können.

So erstellen Sie Box-Plot-Diagramme

Ein Box-Plot-Diagramm erstellt man mit DeltaMaster in drei Schritten:

1. Wir benötigen die fünf statistischen Kenngrößen als eigenständige Analysewerte in unserem Analysemodell. Das ist mit dem entsprechenden Assistenten von DeltaMaster schnell erledigt.
2. Die Analysewerte müssen in eine Pivottabelle übernommen werden. Auch das ist Routine; die Analysewerte werden wie üblich in der Achsendefinition ausgewählt.
3. In der grafischen Darstellung der Pivottabelle (Pivotgrafik) sind ein paar Formatierungen nötig, bis das für Box-Plots typische Bild entsteht. Auch das kostet nur wenige Mausklicks, die allenfalls ein bisschen ungewohnt sind.

Aber der Reihe nach. Der Box-Plot ist eine Pivotgrafik und basiert wie alle Pivotgrafiken auf einer Pivottabelle. Er kann also schon ab der Stufe Pivotizer erstellt werden. Auch die benötigten Analysewerte lassen sich in dieser Stufe anlegen.

Analysewerte anlegen

Die fünf Kenngrößen müssen als Analysewerte (Measures) definiert sein. Sie lassen sich leicht als univariate statistische Analysewerte in DeltaMaster erzeugen (Menü Modell, Neuen Analysewert anlegen).

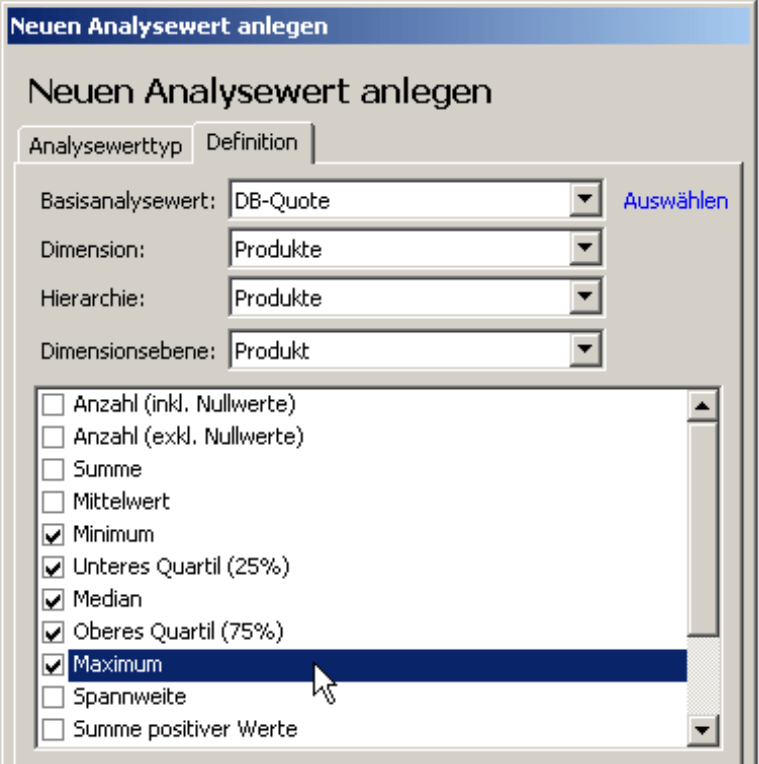
Der Assistent für neue Analysewerte erzeugt alle gewünschten Größen auf einmal. Als Dimension wählen wir diejenige aus, in der sich die zu untersuchenden Elemente verteilen, zum Beispiel Produkte, Kunden, Niederlassungen oder Aufträge. Details zum Umgang mit univariaten statistischen Analysewerten findet man in den DeltaMaster clicks! 07/2009.

Pivottabelle erstellen

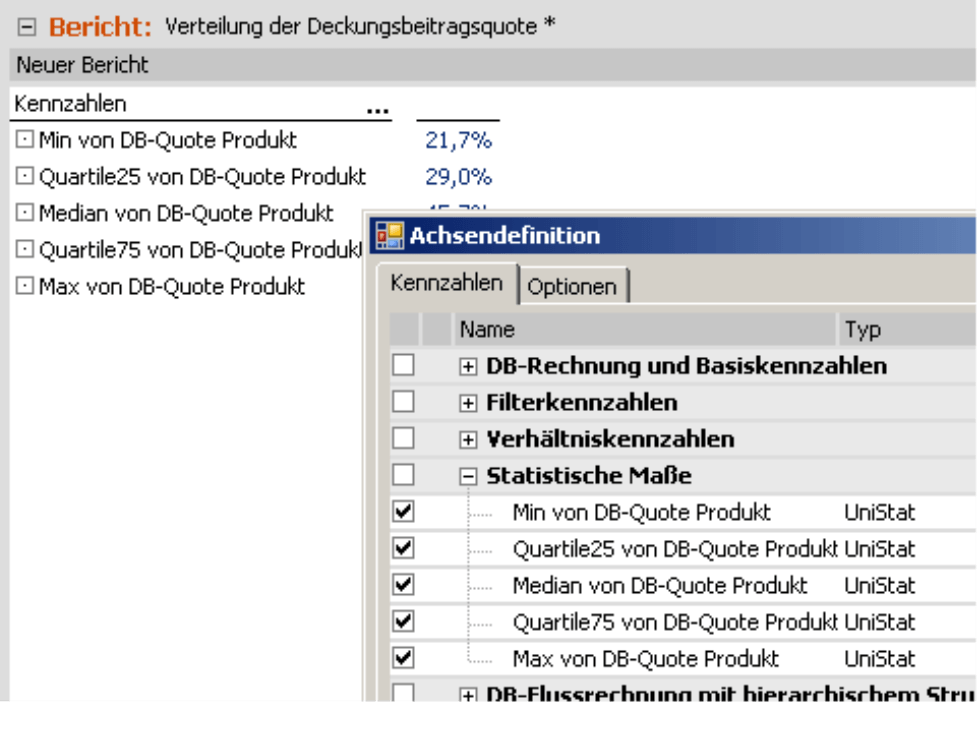
Der Box-Plot setzt einen standardisierten Tabellenaufbau mit diesen fünf Zeilen voraus:

• In der 1. Zeile steht das Minimum,
• in der 2. Zeile das untere Quartil,
• in der 3. Zeile der Median,
• in der 4. Zeile das obere Quartil und
• in der 5. Zeile das Maximum.

In der gleichen Reihenfolge wurden die Werte im Analysewert-Assistenten angeboten und in aller Regel werden sie auch im Analysewert-Browser so angezeigt. Das erleichtert das Auswählen.

Die Spaltenachse kann leer bleiben. Wird sie benutzt, so erzeugt DeltaMaster für jedes Element einen eigenen Box-Plot und stellt diese alle im selben Diagramm nebeneinander dar. Das ermöglicht es, Verteilungsunterschiede zwischen verschiedenen Berichtsgegenständen zu vergleichen, zum Beispiel zwischen Ländern, Niederlassungen, Sortimenten oder Vertragsarten. Legen Sie die Zeitdimension bzw. eine Zeitartendimension („Time Utility“) in die Spaltenachse, so lässt sich beobachten, wie sich die Verteilung über die Zeit ändert.

Datenreihen formatieren

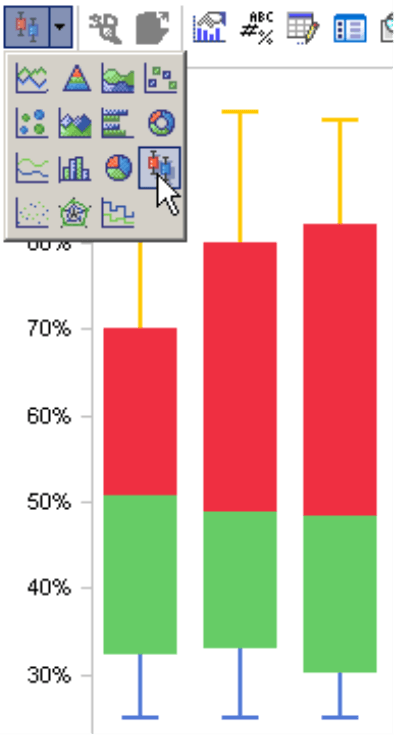
Von der Pivottabelle aus schalten wir über das Menü Ansicht zur Grafik um und öffnen die Werkzeugleiste (Kontextmenü, Menü Ich möchte). In der Auswahl der Grafiktypen findet sich rechts unten der Box-Plot .

Die Darstellung, die wir zunächst erhalten, sieht noch nicht nach einem typischen Box-Plot aus.

Um das übliche umrisshafte Bild zu erhalten, bearbeiten wir die Einstellungen (Kontextmenü) der Datenreihen. Wir beginnen mit der roten Reihe. Aufgrund des standardisierten Tabellenaufbaus steht sie standardmäßig für den Median.

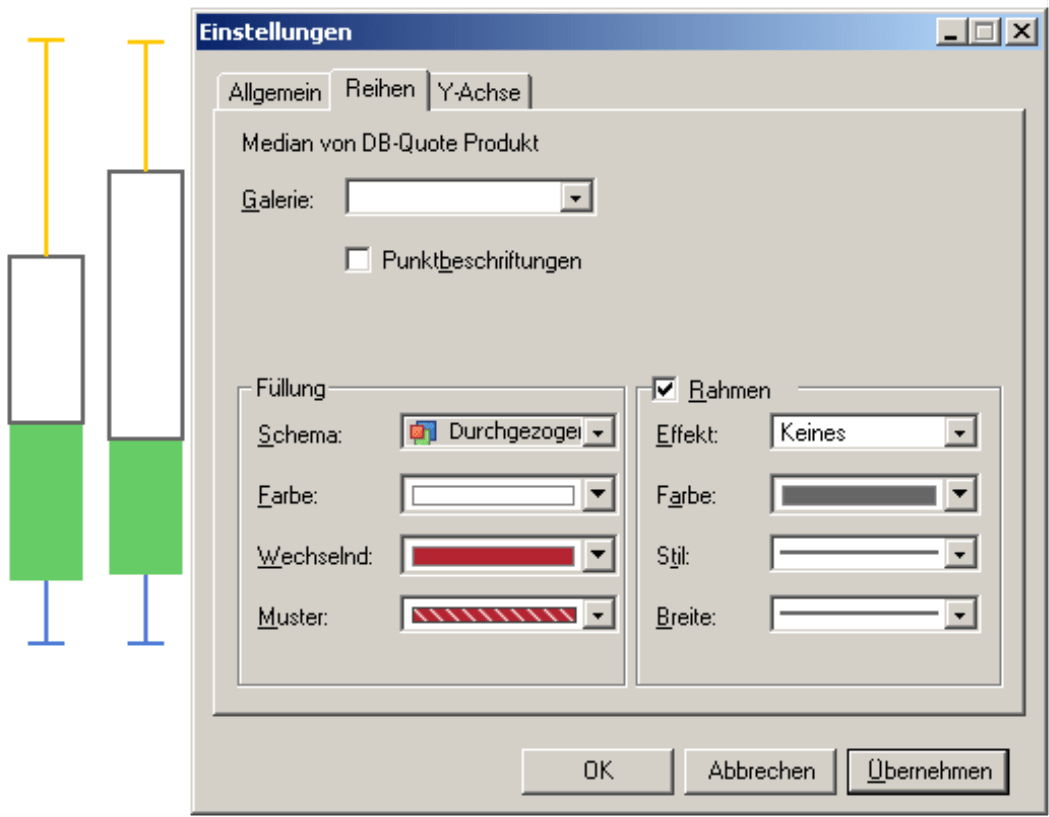
In den Einstellungen auf der Registerkarte Reihen wählen wir für die Füllung die Farbe Weiß. Damit ein Rahmen gezeichnet wird, aktivieren wir das Kontrollkästchen und wählen keinen Effekt; die Farbe des Rahmens stellen wir auf Grau oder Schwarz. Ästheten ändern auch die Breite und wählen die zweitdünnste Strichstärke aus, die der Darstellung der „Antennen“ sehr nahe kommt.

Die gleichen Schritte wiederholen wir für das untere Quartil, das in der Standardansicht grün gezeichnet wird: Füllung mit weißer Farbe, Rahmen mit keinem Effekt in der Farbe Schwarz oder Grau und gegebenenfalls etwas größere Breite.

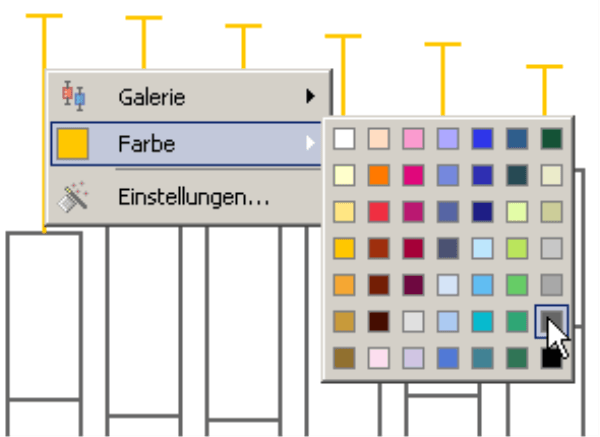
Die Formatierung der „Antennen“ ist einfacher. Da es hier nur auf die Füllung ankommt und nicht auf den Rahmen, genügt das Kontextmenü der Pivotgrafik, um der Reihe eine Farbe zuzuweisen – die gleiche, die wir zuvor für den Rahmen verwendet haben (Schwarz oder Grau).

Auf Wunsch können im Diagramm auch die Zahlenwerte zu den einzelnen Abschnitten angezeigt werden (Kontextmenü der Grafik). Zur Formatierung der Beschriftung können Sie in den Grafikeigenschaften (Kontextmenü, Menü Ich möchte oder Taste F4) die Punktbeschriftungen auf der gleichnamigen Registerkarte bearbeiten. Hier ist es auch möglich, selektiv die Beschriftung für einzelne Analysewerte zu unterdrücken. Häufig kann man beispielsweise auf die Angabe des oberen und unteren Quartils verzichten, während man die Extremwerte und den Median beziffern möchte. Dazu wählen Sie in den Grafikeigenschaften die betreffende Reihe aus, deaktiveren das Kontrollkästchen zum Einblenden der Punktbeschriftung und übernehmen diese Änderung für jede Reihe.

Für Fortgeschrittene

Geübte Nutzer von Box-Plots wünschen sich manchmal, zusätzlich auch den Mittelwert (das arithmetische Mittel) im Diagramm wiederzufinden. Das ist möglich, indem Sie in der Pivottabelle den Mittelwert als sechste Zeile hinzufügen: Die sechste und alle weiteren Zeilen werden als Linien in die Darstellung eingezeichnet. Dies sollten Sie aber nur erfahrenen Lesern anbieten – andere mag die zusätzliche Markierung irritieren, insbesondere dann, wenn das arithmetische Mittel außerhalb der Box liegt, was aufgrund der statistischen Zusammenhänge zwar korrekt und keine Seltenheit wäre, aber unter Umständen erst gelernt werden muss.

Box-Plots verwenden

Der Box-Plot kann für sich als Bericht genutzt und verteilt werden. So können sich auch Anwender auf den Stufen Reader und Viewer mit den Befunden auseinandersetzen. Interessant für Viewer-Anwender: Je nach Einrichtung der Pivottabelle können auch sie interaktiv steuern, welche Box-Plots das Diagramm enthalten soll. Zwei Optionen spielen dafür eine Rolle. Beide sind im Modus Pivotizer oder höher in der Achsendefinition der Spaltenachse festzulegen: Wenn die Achse per Ebenenauswahl (Registerkarte Allgemein) definiert und die dynamische Synchronisation gewählt wurde, können Viewer-Anwender im Fenster Sicht selbst bestimmen, welche Elemente in der Achse anzuzeigen sind – und damit, welche und wie viele Plots im Diagramm erscheinen (siehe auch DeltaMaster clicks! 04/2009). Ist in der Achsendefinition auf der Registerkarte Optionen der Drill-down für den Viewer-Modus zugelassen, lässt sich auf diesem Weg der Diagramminhalt bestimmen (siehe auch DeltaMaster clicks! 06/2009). Der Anwender schaltet dann die Ansicht (Menü im Fenster Bericht) von Grafik auf Tabelle, führt den gewünschten Drill-down aus und wechselt zurück zur Grafik.

Auch in Kombinationscockpits kann man Box-Plots integrieren, wie alle anderen Pivottabellen bzw. ?grafiken. Das empfiehlt sich besonders dann, wenn ein visueller Vergleich mehrerer Analysewerte gefragt ist. Und natürlich lässt sich die Darstellung mit Small Multiples vervielfachen, wie in den DeltaMaster clicks! 11/2009 beschrieben.