Liebe Datenanalysten,

einer der Großen in der Datenvisualisierung ist William Cleveland, neben Jacques Bertin, Otto Neurath, Edward Tufte und Howard Wainer. Ihm ergeht es wie vielen großen Geistern: Seine besten Ideen brauchen am längsten, bis sie Widerhall finden. Dazu gehört eine Idee, wie man Daten grafisch darstellen kann, die erhebliche Größenordnungsunterschiede aufweisen. Seit vielen Jahren schlägt er dazu eine Visualisierung vor, die er „Dot Plots“ nennt.* Im Gegensatz zu Balken können sie logarithmisch skaliert werden – ein bewährtes Verfahren, um Daten über Größenordnungen hinweg vergleichbar wiederzugeben. Für den Logarithmus setzen wir uns schon seit langem ein; jetzt wollen wir auch Cleveland zum Durchbruch verhelfen. Aber natürlich muss es zum Industriereporting passen: zu unserem Ziel, Berichte automatisiert zu produzieren, in gleichbleibender Qualität und ohne Nacharbeit, selbst in hohen Auflagen. Deshalb haben wir Clevelands „Dot Plots“ als neue Option in die Pivottabellen von DeltaMaster integriert. Dort stehen sie Ihnen als „Punktbalken“ zur Verfügung – nicht nur für die kniffeligen Fälle der Visualisierung, sondern als universelles Gestaltungsmittel auch für weniger aufregende Datenkonstellationen. Wie Sie die Punktbalken nutzen und warum sie den normalen Balken überlegen sind, erläutern wir in diesen DeltaMaster clicks!.

Herzliche Grüße
Ihr Team von Bissantz & Company

* William S. Cleveland, The Elements of Graphing Data, Murray Hill 1994.

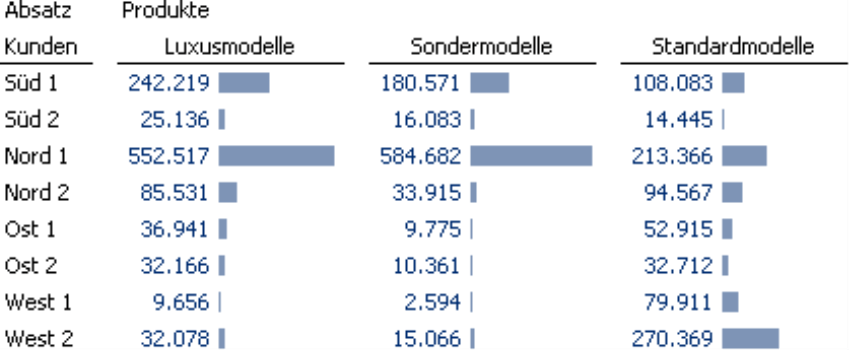
Seit DeltaMaster 5.4.9 beherrschen die Pivottabellen einen neuen Typ von Zellgrafiken: Punktbalken, rechts abgebildet, und Punktsäulen. Diese noch recht jungen Darstellungsformen veranschaulichen die Wertverhältnisse in der Tabelle. Zu lesen sind Punktbalken ganz einfach: Der abzubildende Wert wird als ein Punkt auf einer dünnen Hilfslinie eingetragen; diese repräsentiert die Spannweite aller Werte in der Tabelle, der jeweiligen Spalte oder der jeweiligen Zeile (siehe unten).

Auf den ersten Blick könnte man meinen, es handele sich lediglich um eine grafische Variation der bekannten Balken, die die Pivottabellen von DeltaMaster zu Grafischen Tabellen machen. Bei Punktbalken wird nicht ein ganzer Balken gezeichnet, sondern nur dessen äußere Kante, in Form eines Punktes. Das macht die Darstellung luftiger – oder, wie Edward Tufte es vielleicht sagen würde: Sie benötigt weniger „Tinte“. Und allein der Umstand, dass die Darstellung neu und noch wenig verbreitet ist, dürfte ihr eine gewisse zusätzliche Aufmerksamkeit bescheren. Das wären immerhin zwei Pluspunkte im Vergleich zu Balken. Aber es steckt mehr dahinter!

Der große Vorteil von Punktbalken ist nämlich: Sie lassen sich flexibel skalieren. Deshalb behaupten sie sich auch in schwierigen Datenlagen, etwa bei relativ geringen Wertunterschieden auf einem hohen Grundniveau oder bei unterschiedlichen Größenordnungen innerhalb einer Datenreihe. Das macht sie zu einer ausgesprochen vielseitigen Visualisierungsform – und zu einem dankbaren Thema für diese DeltaMaster clicks!. Der Einfachheit halber konzentrieren wir uns auf Punktbalken; für Punktsäulen gelten die folgenden Ausführungen analog.

Punktbalken einfügen

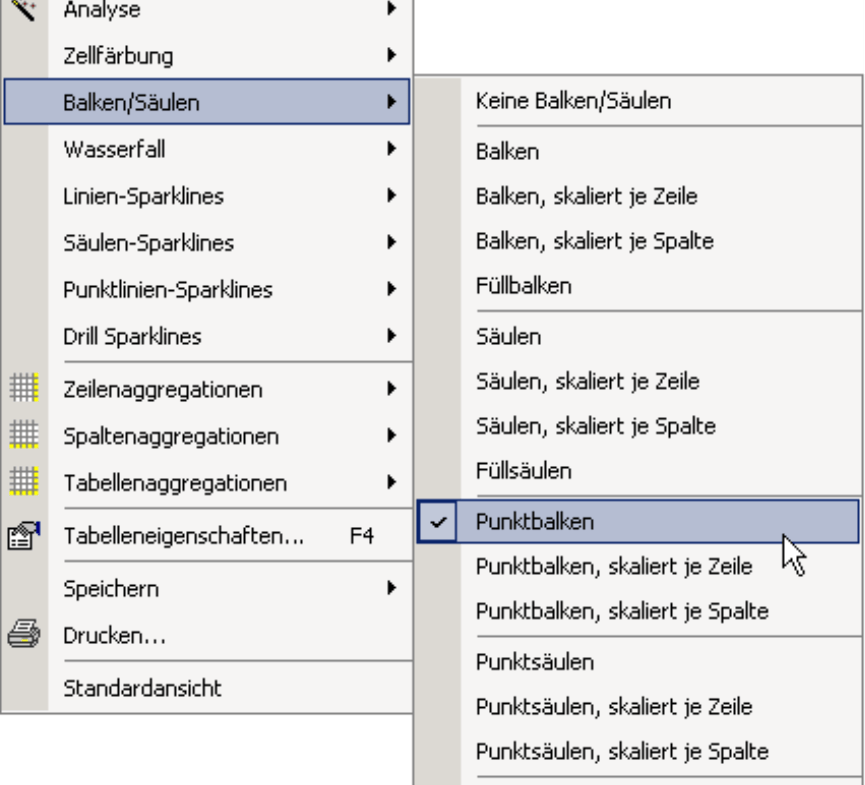
Punktbalken werden so in die Tabelle eingefügt, wie Sie es von den Balken her kennen – über den Eintrag Balken/Säulen im Kontextmenü der Pivottabelle. Das ist in allen Benutzerstufen möglich, vom Reader bis zum Miner. Auch die Skalierungsoptionen im Kontextmenü sind Ihnen vertraut: Die Punktbalken können in der gesamten Tabelle oder je Spalte oder je Zeile in einem einheitlichen Maßstab gezeichnet werden.

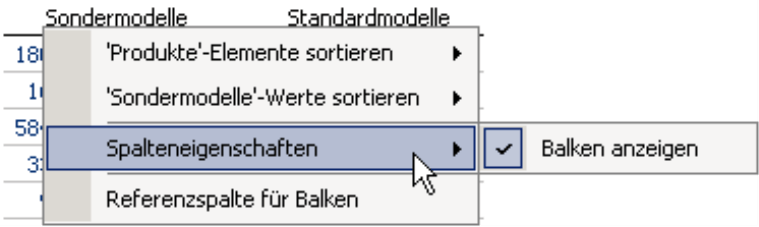
Die Visualisierung wird zunächst für die gesamte Tabelle aktiviert, anschließend lässt sie sich für einzelne Spalten bzw. Zeilen wieder ausblenden (Spalteneigenschaften im Kontextmenü des Spaltenkopfs bzw. Zeileneigenschaften im Kontextmenü der Zeilenbeschriftung) – auch dies wahrscheinlich nichts Neues für Sie, wenn Sie schon einmal mit den Grafischen Tabellen von DeltaMaster gearbeitet haben.

Skalierung und andere Tabelleneigenschaften

Der Clou an Punktbalken ist, dass sie sich skalieren lassen wie Liniendiagramme. Das ist bei Balken nicht möglich. Warum das so ist: dazu gleich mehr.

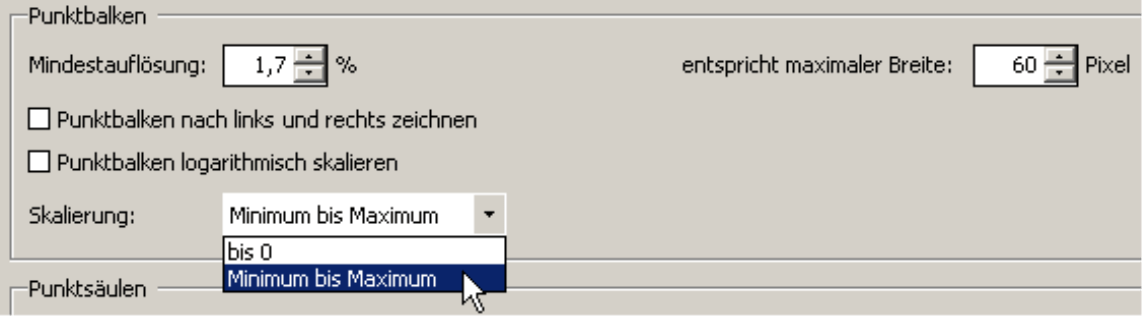
Die Skalierungsoptionen finden Anwender der Stufen Pivotizer, Analyzer und Miner in den Tabelleneigenschaften (Kontextmenü, Menü Ich möchte oder Taste F4) auf der Registerkarte Grafische Elemente (1). Hier wählt man, ob DeltaMaster die Punktbalken logarithmisch skalieren soll (statt linear) und ob die Skalierung nur die Werte zwischen dem kleinsten und dem größten Wert des Bezugsbereichs berücksichtigt (Minimum bis Maximum, vulgo: „Achsen abschneiden“) oder stets die Nulllinie einbezogen wird (bis 0).

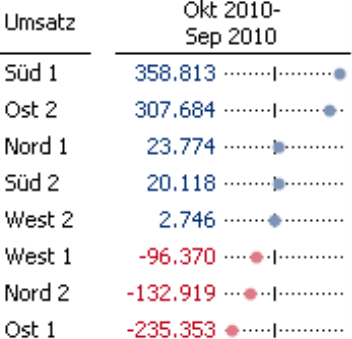
Außerdem werden hier zwei weitere Optionen angeboten: Zum einen lässt sich die maximale Breite der Punktbalken in Pixeln vorgeben (und, damit korrespondierend, die Mindestauflösung). Zum anderen können Sie einstellen, dass Punktbalken nach links und rechts gezeichnet werden sollen. Das ist für Berichte interessant, in denen positive und negative Werte gemeinsam auftreten können, zum Beispiel bei Plan-Ist-Abweichungen oder Vorperiodenveränderungen. Ist die Option aktiviert, fügt DeltaMaster eine kleine senkrechte Markierung für die Null ein.

Warum aber sollten wir die Skalierung von Punktbalken ändern wollen – und warum geht das nicht bei Balken? Das hängt zusammen mit der Deutungspriorität.

Deutungspriorität

Die Deutungspriorität beschreibt, woran sich unser Auge orientiert, wenn es die grafischen Elemente eines Diagramms in Zahlen und Zahlenverhältnisse „übersetzt“.

• Bei Balken und Säulen achtet das Auge auf die Länge der Balken bzw. auf die Höhe der Säulen und somit auf den Abstand der Datenpunkte zu einer Nulllinie.
• Bei Liniendiagrammen hingegen achtet das Auge vor allem auf den Abstand zwischen den einzelnen Datenpunkten, also auf die Steigungen der Liniensegmente von einem Punkt zum nächsten. Das Auge gleitet förmlich über die Linie wie beim Blick über einen Bergkamm und vergleicht die Höhenunterschiede zwischen Gipfeln und Tälern, unabhängig von ihrem Abstand nach unten.

Diese Erkenntnis hat gravierende Auswirkungen auf die Konstruktion von Diagrammen.

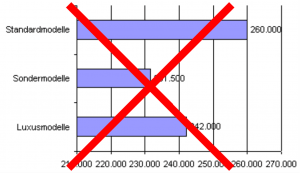
So geben Balken und Säulen die Wertverhältnisse verzerrt wieder, wenn man sie verkürzt – wenn man also einen „Sockelbetrag“ abzieht und nur den Bereich zeichnet, in dem sich die Werte verändern, etwa zwischen Minimum und Maximum der Datenreihe. Bei einer „abgeschnittenen Achse“ sind die Wertunterschiede nicht mehr proportional zur Länge der Balken oder zur Höhe der Säulen, und auf die kommt es dem Auge bei dieser Darstellungsform ja an. (Deshalb ist es ärgerlich, dass Microsoft Excel in allen aktuellen Versionen bei eng zusammen liegenden Werten automatisch die Achsen beschneidet, wenn man nicht explizit in jedem einzelnen Diagramm etwas dagegen unternimmt.) In der Abbildung sehen wir, dass der Balken für die „Standardmodelle“ mehr als doppelt so lang ist wie der der „Sondermodelle“, obwohl der Wertunterschied bei gerade einmal 12 Prozent liegt.

Bei Linien verhält es sich anders: Hier liegt die Deutungspriorität nicht auf dem Abstand zur Achse, sondern auf den Abständen zwischen den einzelnen Punkten. Zieht man überall einen Sockelbetrag ab und beschneidet dadurch die Achse, so wirken die Abstände von Punkt zu Punkt vielleicht dramatischer – aber sie werden immer noch korrekt wiedergegeben und nicht verzerrt. Bei größeren Wertunterschieden skaliert man die Y-Achse logarithmisch, sodass gleiche prozentuale Unterschiede von einem Punkt zum nächsten immer mit der gleichen Steigung dargestellt werden, bei großen wie bei kleinen Werten. Über die Vorzüge, ja: über die Notwendigkeit einer logarithmischen Skalierung hatten wir ausführlich in den DeltaMaster clicks! 07/2010 geschrieben. Die logarithmische Skalierung funktioniert jedoch nur bei Linien; bei Balken und Säulen hingegen würde unser Auge wieder die absoluten Längen und Höhen beachten und könnte die relativierende Wirkung des Logarithmus nicht erkennen.

Was die Skalierung angeht, sind Linien also deutlich flexibler als Balken und Säulen. Aber: Linien sind reserviert für die Zeit! Wir würden unsere Leser nur verwirren, zeichneten wir einen Strukturvergleich als Linie – ein Diagramm, das für nur eine Periode die Umsätze verschiedener Vertriebsregionen oder Produktgruppen als Linie repräsentierte, wäre kaum zu verstehen.

Und damit sind wir bei Punktbalken: Für sie gilt die gleiche Deutungspriorität wie für Linien. Auch wenn keine Verbindungslinie eingezeichnet ist, lesen wir sie wie die Punkte in einem Liniendiagramm; wir verfolgen die Abstände von Punkt zu Punkt, der Abstand zu einer Nulllinie tritt in den Hintergrund. Deshalb können wir skalieren wie bei Liniendiagrammen – und das heißt insbesondere: Wir können Achsen abschneiden, damit die Darstellung besser differenziert, und wir können sie logarithmisch skalieren, um relative Wertunterschiede herauszuarbeiten, auch bei Werten unterschiedlicher Größenordnung.

Skalierungsvarianten im Vergleich

Wenden wir also die Skalierungsoptionen logarithmisch und von Minimum bis Maximum auf einen Beispieldatensatz an: auf die Produktgruppen in unserem Referenzmodell „Chair“. Wohlgemerkt, für normale Balkendarstellungen kommen beide Skalierungsvarianten nicht infrage, da aufgrund der Deutungspriorität eine Verzerrung entstünde. Deshalb bietet DeltaMaster diese Optionen für normale Balken gar nicht erst an.

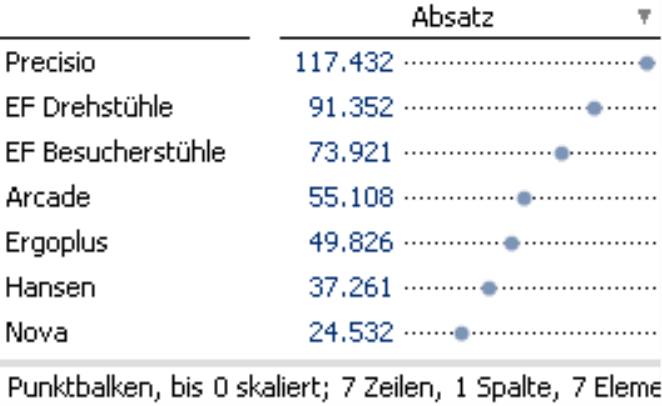
In der herkömmlichen Skalierung (linear, bis 0) gibt die Lage der Punkte rechts von der vertikalen Grundlinie die absoluten Wertverhältnisse proportional wieder. Die Punktbalkenbreite ist hier auf 100 Pixel eingestellt.

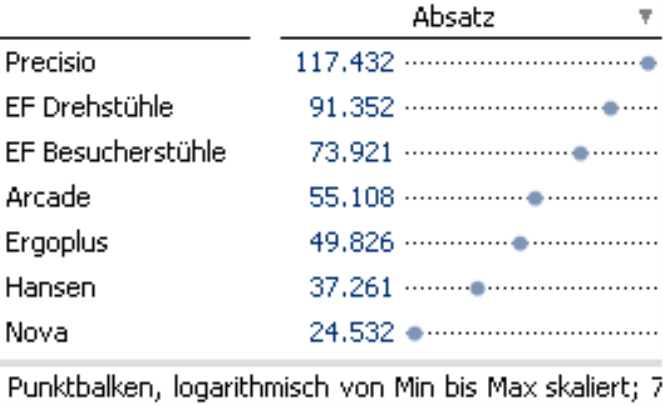
Wenn wir zwischen Minimum und Maximum skalieren, wird der kleinste Wert ganz links im Zeichenbereich angeordnet und der größte ganz rechts. Die Abstände machen absolute Wertunterschiede vergleichbar: Der Abstand von 24.532 zu 49.826 ist ungefähr so groß wie der zwischen 49.826 und 73.921, nämlich jeweils rund 25.000. Die Skalierung zwischen Minimum und Maximum verbessert die Differenzierung und sorgt dafür, dass kleine Veränderungen auch auf durchgängig hohem Niveau noch zu erkennen sind, weil für den gleichen absoluten Wertunterschied wie im ersten Bild mehr Pixel zur Verfügung stehen.

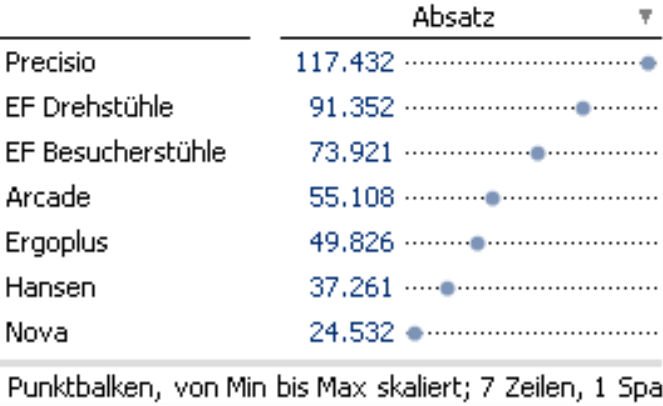
Die logarithmische Skalierung schließlich macht relative Wertunterschiede vergleichbar: Gleiche Punktabstände stehen für den gleichen prozentualen Unterschied, das heißt den gleichen Faktor zwischen den Werten. Der Abstand von 24.532 zu 49.826 ist ungefähr so groß wie der zwischen 49.826 und 91.352 (nämlich jeweils ungefähr doppelt so groß, großzügig gerundet).

Die gewählte Skalierung wird in der Statusleiste unterhalb des Berichts angegeben, im Präsentationsmodus unter der Überschrift, damit der Leser die Darstellung korrekt interpretieren kann.

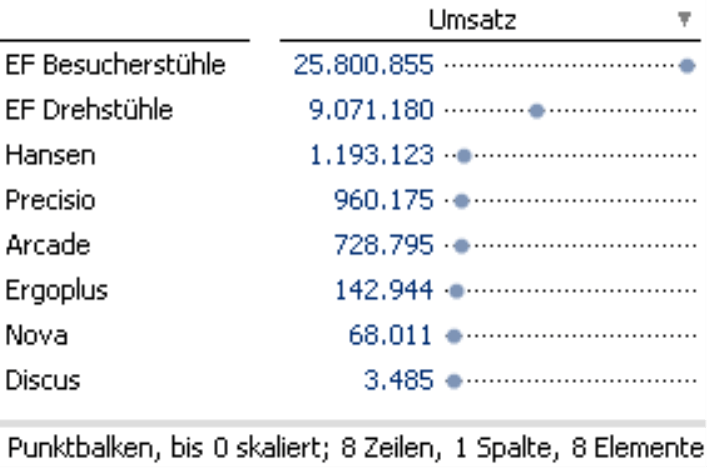
Auch in Fällen, in denen die Werte stark streuen, eignet sich die logarithmische Skalierung. In der Praxis ist das nicht selten: Mit einem oder wenigen Großkunden erzielt man den Großteil des Umsatzes, die anderen folgen mit weitem Abstand; das Stammhaus in Deutschland beschäftigt zigmal mehr Mitarbeiter als die neu gegründete Tochter in Malaysia usw. Visualisiert man solche Datenlagen mit Balken, sind Unterschiede zwischen den kleinen Objekten nicht mehr zu erkennen; diese werden von den großen regelrecht „zusammengequetscht“.

Mit einer logarithmischen Skalierung kann man dem begegnen.

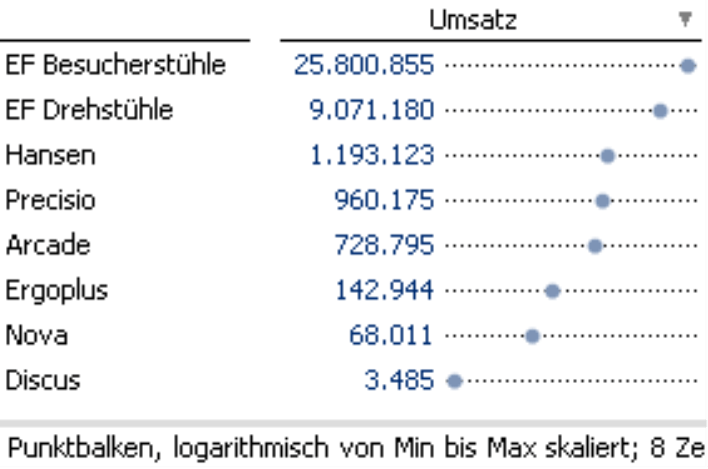
Die logarithmische Skalierung (rechts) macht die relativen Unterschiede vergleichbar: Der Umsatz mit „Ergoplus“ ist zwei- bis dreimal größer als der mit „Nova“ und ebenso ist der Umsatz mit den „EF Besucherstühlen“ zwei- bis dreimal größer als der mit den „EF Drehstühlen“. Dass diese Wertpaare ein ähnliches Verhältnis haben, ist in der Tabelle jetzt mit bloßem Auge zu erkennen. Wer nachrechnet, findet diese Beobachtung bestätigt („Ergoplus“ : „Nova“ = 2,1, „EF Besucherstühle“ : „EF Drehstühle“ = 2,8).

Gruppierung

Und einen weiteren Vorteil logarithmisch skalierter Punktbalken macht die rechte Abbildung deutlich: Die Lage der Punkte führt zu einer gewissen Gruppierung. Dicht zusammen liegen die Spitzenprodukte „EF Besucherstühle“ und „EF Drehstühle“, die beide für Millionenumsätze gut sind. „Hansen“, „Precisio“ und „Arcade“ sind eine zweite Gruppe, mit hohen sechsstelligen Umsätzen bis knapp über die Million. „Ergoplus“ und „Nova“ bilden eine weitere Gruppe, „Discus“ ist klares Schlusslicht. All dies geht in der linken Abbildung unter – durch die lineare Skalierung sieht man nur noch ein, zwei bedeutende Objekte, die alles andere überlagern, als ob zwischen diesen keine Unterschiede mehr wären.