Im zweiten Teil der Blogbeitragsreihe „Freie Wetterdaten“ widmen wir uns dem Thema Modellieren und Analysieren. Nachdem wir im ersten Teil die historischen Wetterdaten der Wetterstationen des Deutschen Wetterdienstes importiert haben, analysieren wir diese und ergänzen die vorhandenen Merkmale um nützliche neue Perspektiven. Ziel ist es, so viel wie möglich mit der richtigen Modellierung aus den Daten herauszuholen, um anschließend in der Analyse und dem Reporting möglichst viele der aufkommenden Fragestellungen beantworten zu können.
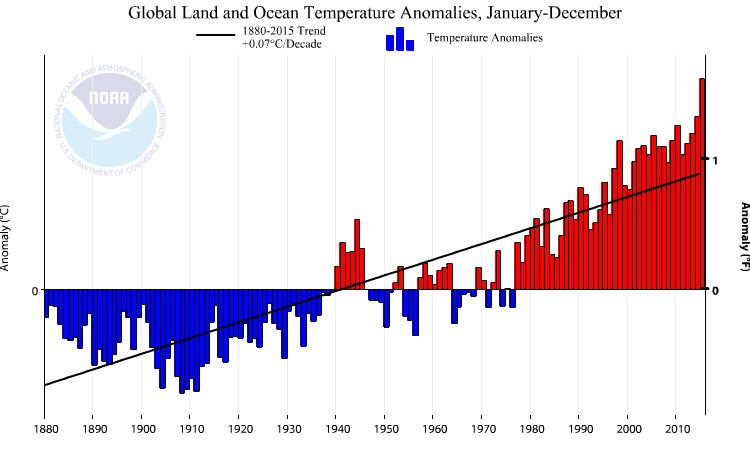
Es geht weiter mit dem spannenden Thema Wetter bzw. Klima. Denn nicht nur sehen wir im Wetter ein nettes Thema für den Smalltalk zwischendurch, sondern müssen mit Besorgnis konstatieren, dass der Klimawandel (wie leider immer noch manche Leute nicht glauben) real ist, mit zum Teil dramatischen Folgen. Diese Veränderung im Klima wird natürlich nicht nur subjektiv wahrgenommen, sondern sollte viel wichtiger mit Fakten und Daten belegt werden. Für die Erhebung sind Einrichtungen wie der Deutsche Wetterdienst oder die US-Klimabehörde NOAA zuständig. Letztere meldete erst im Januar, dass das Jahr 2016 das wärmste seit Beginn der Wetteraufzeichnungen war. Damit stellt das Jahr 2016, nach den Temperaturrekorden der Jahre 2014 und 2015, das dritte Rekordjahr in Folge dar. Ein bedenklicher Trend wie es scheint, der von den Behörden auch grafisch festgehalten wird. Was uns hier nebenbei erfreut, sind natürlich die eingesetzten Farben, die in der Visualisierung der Temperaturabweichung (kälter = blau; wärmer = rot) von der globalen Durchschnittstemperatur in doppelter Hinsicht Sinn machen.
Abbildung 1: Quelle: NOAA
Nachdem wir im letzten Teil dieser Reihe gezeigt haben, wie wir Wetterdaten des Deutschen Wetterdiensts anbinden können, wollen wir bei diesem Schritt natürlich nicht stehen bleiben. Der Reiz, diese Daten zu analysieren, ist zu groß. Deshalb werden wir uns in diesem Teil der Analyse sowie der vo-rausgehenden Modellierung widmen. Damit sollten wir die Möglichkeit erhalten, zu prüfen, ob dieser globale Trend auch in Deutschland nachvollziehbar ist.
Modellierung
Durch die im Teil 1 gezeigten Importprozesse der Wetterdaten stehen uns nun die angebundenen Daten zur Verfügung. Diese bestehen zum einen aus den Stammdaten der Wetterstation und zum anderen aus den Bewegungsdaten der Wetteraufzeichnung.
Dabei enthalten die Wetterstations-Stammdaten folgende Informationen zur geografischen und topografischen Lage, sowie zum Einsatzzeitraum der Wetterstation:
- Stations_ID
- von_datum
- bis_datum
- Stationshöhe
- geoBreite
- geoLänge
- Stationsnamen
- Bundesland
Die Bewegungsdaten enthalten neben dem Bezug zur Wetterstation zurzeit keine weiteren Merkmale, bis auf eine Klassifizierung des Qualitätsniveaus. Alle anderen Informationen der Datensätze stellen Messwerte dar:
- Stations_ID
- Mess_Datum
- Qualitäts_Niveau
- Lufttemperatur
- Dampfdruck
- Bedeckungsgrad
- Luftdruck_Stationshöhe
- Rel_Feuchte
- Windgeschwindigkeit
- Lufttemperatur_Max
- Lufttemperatur_Min
- Lufttemp_am_Erdb_Min
- Windspitze_Max
- Niederschlagshöhe
- Niederschlagshöhe_Ind
- Sonnenscheindauer
- Schneehöhe
Nun scheint die Auswahl der Merkmale, bestehend aus Wetterstation und der Zeit (das Qualitätsniveau wird hier mal außer Acht gelassen), wenig Potential für die spätere Analyse zu bieten. Jedoch sollten wir uns, bevor wir hier vorschnell urteilen, die beiden Merkmale genauer anschauen.
Die Zeit/Periode
Eine Analyse
Der Zeit wird in der OLAP-Welt eine besondere Rolle zu Teil. Sie ist das maßgebende Merkmal, auf dem viele Logiken fußen. Seien es abhängige Dimensionen, wie die Kumulation oder die Periodenansicht, die ohne Zeitbezug nicht existieren würden, oder eine ganze Reihe von MDX-Syntax, die nur mit der Zeit-Dimension zusammenspielen (PeriodstoDate, ParallelPeriod etc.) können. Die Zeit ist das Fundament jeder Analyse. Deshalb erstellt der DeltaMaster Modeler auch ganz automatisch diese Dimension, sowie dessen abhängige Dimensionen.
Auch bei Wetter- und Klimadaten ist das nicht anders. Im Gegenteil, hier ist diese Dimension noch wichtiger zu beurteilen. Da sich die Wetteraufzeichnungen über einen langen Zeitraum von über 100 Jahren erstrecken, wird im Kontrast zu Unternehmenszahlen, die meist nicht mehr als 10 Jahre umfas-sen, eine weitere Verdichtungsebene über der Jahresebene notwendig.
Wie man bereits schön an der Zeitachse der oben aufgezeigten Grafik erkennt, spielen bei Klima- bzw. Wetterdaten gerade die Dekaden eine große Rolle, da sich die klimatischen Bedingungen relativ lang-sam verändern. Deswegen macht es Sinn, die Zeit-Dimension dahingehend auszubauen.
Hinzu kommt aber noch ein anderes Problem. Denn typische analytische Fragen bezogen auf die Wetterdaten können mit der Standardzeit-Dimension nicht beantworten werden. Darunter fallen Fragen wie: „In welchem Jahr war in Deutschland der heißeste Sommer?“ oder „Welcher Monat ist durchschnittlich der kälteste in Deutschland?“. Hier kommen wir mit der Verdichtung Tag-Monat-Quartal-Jahr-Jahrzehnt nicht weiter.
Viel eher müssen wir eine zusätzliche Hierarchie schaffen, die genau diese Fragen beantworten kann. Dazu werden erstmal, wie gewohnt, die Tage den Monaten zugeordnet. Anschließend werden jedoch die Monate auf nächsthöherer Ebene ohne Bezug zum Jahr verdichtet, wodurch beispielsweise die Juni-Monate aller Jahre zum neuen Verdichtungselement „Juni“ zusammengefasst werden. Dadurch wird es möglich, die Daten für den spezifischen Monat über den gesamten Wetteraufzeichnungszeitraum bzw. für einen Ausschnitt zu analysieren. Darauf aufbauend, können dann die Monate ohne Jahresbezug wiederum den meteorologischen Jahreszeiten zugeordnet werden.
Dadurch werden folgerichtig der Dezember, der Januar und der Februar der Winter-Jahreszeit zugeordnet. Schlussendlich können wir nun über die zusätzliche Hierarchie in Kombination mit der erweiterten Standardzeit-Hierarchie ein deutlich größeres Fragenspektrum beantworten.
Dimensionsaufbau
Einer unter vielen Annehmlichkeiten des Modeler ist die automatische Generierung der Perioden so-wie der dazugehörigen Standarddimensionen. Bei der Perioden-Dimension wird, im Gegensatz zum gewöhnlichen Projektvorgehen, die Quelltabelle in einer View für die Dimensions-Tabelle vorzuberei-ten, direkt auf die Quelltabelle (hier: T_S_Periode) zugegriffen. Die Quelle der einzelnen ID und Na-mensspalten der Ebenen wird dann über die Funktion F_BC_DateID bzw. F_BC_DateCode generiert. Nun wäre es möglich die Erweiterung, die bereits in der Analyse besprochen wurde, mit in die Funkti-on aufzunehmen. Alternativ und wohl auch die schnellere Option ist, auf die Tabelle T_S_Periode eine View zu setzen, in der die Erweiterung mitaufgenommen werden. Die SQL-Syntax dieser View sieht folgendermaßen aus:
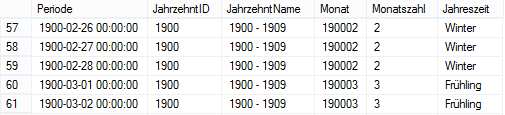
Um die JahrzehntID zu generieren, nutzen wir das Jahr (über Datepart(yyyy,Periode)), welches wir über Round(Jahr,-1,1) dann an der ersten Stelle vor dem Komma (-1) kürzen (3. Parameter muss hier ungleich 0 sein) anstatt zu runden. Die gleiche Syntax können wir auch für die Benennung verwenden. Folgendes Ergebnis erhalten wir schlussendlich aus der View:
Abbildung 2: Ergebnis View
Im Modeler muss nun nur noch die Quelltabelle geändert, sowie die Jahrzehnte als weitere Ebene mitaufgenommen werden.
Abbildung 3: DeltaMaster Modeler
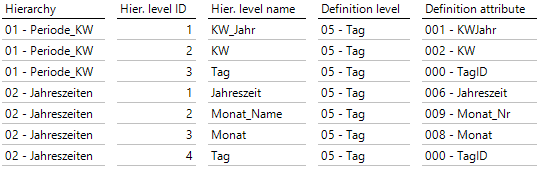
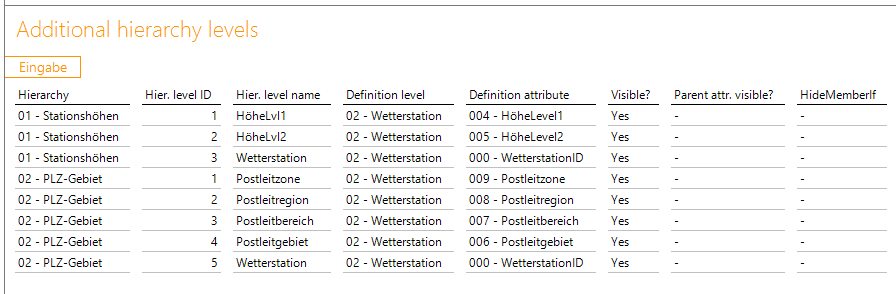
Für die Jahreszeiten erstellen wir eine zusätzliche Hierarchie unter „Additional hierarchies“ und bauen die Ebenen wie folgt auf:
Abbildung 4: DeltaMaster Modeler
Mit diesen Anpassungen stehen uns die gewünschten Erweiterungen dann anschließend zur Verfügung.
Die Wetterstation
Die Wetterstation
Eine Analyse
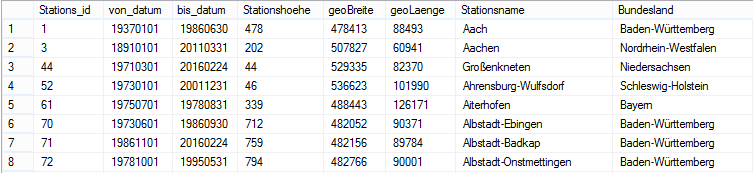
Die Daten zur Wetterstation bieten neben dem Schlüsselfeld und dem Namen der Station selbst schon einige interessante Zusatzinformationen, die hierarchisch oder als Attribut genutzt werden können.
Abbildung 5: Zusatzinformationen
Zu diesen zählt die Stationshöhe, die Breiten- und Längengrade sowie das Bundesland. Das von_datum und bis_datum kann ebenso zu informativen Zwecken als Attribut aufgenommen werden.
Jeder Verfechter der Geo-Analyse wird bei den Worten Längen- und Breitengraden innerlich schon Luftsprünge machen und sich auf die Auswertung freuen. Dementsprechend ist die Aufnahme dieser Informationen als Attribut relativ eindeutig. Auch die geografische Einteilung nach Bundesland ist eine willkommene Gruppierungsmöglichkeit für die Wetterstationen. Mit Hinblick auf die spätere Analyse der Wetterdaten sollte jedoch auch eine andere Information unser Interesse wecken, nämlich die Höhenangabe der Station. Durch die geografische Betrachtung nach Bundesländern haben wir die Möglichkeit, Werte (Temperatur, Niederschlag etc.) auf Bundeslandbasis zu errechnen und diese miteinander zu vergleichen.
Jedoch werden bei dieser Sicht Wetterstationen zusammengefasst, die an Orten stehen, an denen sehr unterschiedliche klimatische Bedingungen herrschen. Man denke nur an die Wetterstation auf der Zugspitze und im Vergleich dazu eine in Hamburg. Dementsprechend kann es sinnvoll sein, um klimatisch vergleichbare Wetterstationen zu gruppieren, diese nach der Wetterstationshöhe ergänzend zu klassifizieren. Damit lassen sich anschließend Wetterstationen auf einem ähnlichen Höhenniveau nach den Messwerten vergleichen, wodurch eine relativ homogene Gruppierung geschaffen wird.
Optional wäre auch eine Klassifizierung der Wetterstationen nach den Klimazonen, in denen sie sich befinden, denkbar. Für eine geografisch etwas feinere Gruppierungsmöglichkeit als direkt das Bundesland, nutzen wir bei Unternehmensdaten gerne die Einteilung in PLZ-Regionen, -Gebiete, und -Zonen. Was uns hierfür jedoch fehlt, ist die Postleitzahl der Wetterstationen. Uns steht lediglich der Wetter-stationsname zur Verfügung. Jedoch sind die Wetterstationen nach ihrem Standort benannt, was eine Zuordnung vielleicht möglich macht.
Dimensionsaufbau
Die Analyse der Daten führt uns nun bereits die unterschiedlichen hierarchischen Möglichkeiten auf, die wir nun über unseren Standardansatz der vorgelagerten „V_Import“-View umsetzen wollen. Im Standardrepertoire des Modeler sind für die geografische Einordnung von Standortinformationen nützliche Tabellen enthalten. Diese sind entweder unter „T_S_Geo“ oder „T_Import_Geo“ zu finden und beinhalteten zum einen die Kreis-Sicht (bis hoch zum Bundesland) sowie die Postleitzahl-Sicht.
Da wir zum einen die Bundesländer als Verdichtungsebene über den Wetterstationen nutzen wollen, zum anderen aber auch nach Postleitgebieten analysieren wollen, benötigen wir hier beide Hilfstabellen zu Anreicherung. Wie wir jedoch schon zuvor festgestellt haben, ist gerade die Anreicherung der Wetterstationsdaten um die PLZ-Daten nicht ohne weiteres möglich. Das einzige Merkmal, das hier genutzt werden kann, ist der Stationsname, welcher meist nach dem Standort benannt wurde.
Jedoch müssen wir für ein Mapping der Daten die Wetterstationsnamen per SQL umbauen, um möglichst viele Übereinstimmungen zu erreichen. Dafür analysieren wir zuerst den Datenbestand. Auffällig ist hier, dass der Stationsname entweder rein aus der Stadt/Dorf-Bezeichnung besteht oder, wenn es mehrere Wetterstationen dort gibt, mit einer Zusatzbenennung unterschieden wird. Diese sind jedoch meist nach einem gewissen Muster aufgebaut und können so über ein CASE-Statement angepasst werden, welches wie folgt aussieht und in ein vorgelagertes WITH-Statement ausgelagert ist:
Im Case-Statement zur Ermittlung des Postleitgebietes wird dann meist ab einem bestimmten Zeichen, wie dem Bindestrich, der Wetterstationsname abgeschnitten, um die Zusatzbenennung zu eliminieren. Zudem wird der Ortzusatz „Bad“, welcher im Wetterstationsnamen hinten angeführt wird, nach vorne geholt. Die Reihenfolge der CASE-Statements ist hier ebenso von entscheidender Bedeu-tung, da die meisten Cases hier auf mehrere Datensätze zutreffen. In dieser gewählten Konstellation kommt es dann zu den meisten Übereinstimmungen, die es uns ermöglichen zumindest 865 Wetter-stationen der insgesamt 1065 dem richtigen Postleitzahlgebiet zuzuordnen.
Zusätzlich zur Anpassung des Wetterstationsnamens bauen wir im WITH-Schritt bereits die anderen Hierarchien auf. Dazu gehört auch die Stationshöhe, die wir in drei Ebenen unterteilen. Zum einen sollen alle, die auf zwei Stellen vor dem Komma gerundet die gleiche Stationshöhe haben, zusammen-gefasst werden und darüber hinaus die, die auf drei Stellen vor dem Komma die gleiche Stationshöhe haben. Der Längengrad sowie der Breitengrad verfügen in der T_Import-Tabelle noch nicht über eine Dezimaltrennung. Diese muss nun durch das Replace-Statement noch künstlich nach der vierten Stel-le von rechts gesetzt werden. Zudem holen wir uns nun aus der zuvor schon angesprochenen T_IMPORT_GEO_DKKRE1112 die Bundesland_ID, um die Geo-Analyse auf Bundeslandebene durchführen zu können.
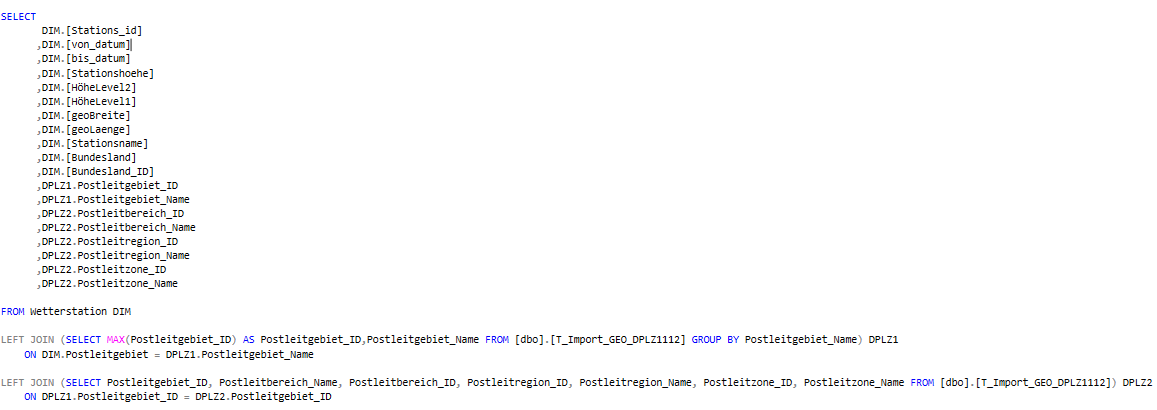
Im letzten Schritt müssen wir nun über das Mapping per Left Join auf die zuvor erwähnte Tabelle T_Import_GEO_DPLZ1112 das richtige Postleitgebiet hinzuholen. Da es jedoch für eine Stadt bzw. einen Landkreis mehrere Postleitzahlen geben kann, müssen wir uns hier über die Gruppierung (Postleitgebietnamen) im Left Join eine PLZ bestimmen (per MAX auf die Postleitgebiet_ID). Diese Annah-me muss getroffen werden, um eine Eindeutigkeit herzustellen. Anschließend können dann über den zweiten Left Join und der eindeutigen Postleitgebiet_ID, die darüber liegenden Ebenen Postleitbereich, Postleitregion und Postleitzone hinzugeordnet werden. Somit stehen uns nun alle Spalten für das Modellieren der Hierarchien zur Verfügung.
Die Haupthierarchie wird die Einteilung nach Bundesland, welche wie folgt modelliert wird.
Abbildung 6: Modellierung Haupthierarchie
Für die spätere Nutzung bei der Geo-Analyse werden die Geo-Koordinaten als Attribute aufgenommen.
Als „additional hierarchies“ werden dann noch die beiden Hierarchien „Stationshöhen“, sowie „PLZ-Gebiet“ mit den folgenden Ebenen aufgebaut:
Damit verfügen wir dimensional schlussendlich über die gewünschten Ausprägungen und das Analysepotential, um den Daten auf den Grund zu gehen.
Die Kennzahlen
Wie wir bereits in der Einleitung des Modellieren-Teils gesehen haben, verfügen wir über eine größere Auswahl an Messwerten, die Bestandteil der Wetteraufzeichnungen sind. Von verschieden gemessenen Temperaturdaten (Temperatur_Max, Temperatur_Min) über unterschiedliche Niederschlagsdaten (Niederschlagshöhe, Schneehöhe) bis hin zu Windgeschwindigkeiten und Sonnenscheindauern.
Eine Charakteristik haben sie dabei alle gemein: Eine Summierung dieser Daten als Aggregationstyp würde keine nennenswerte Aussage mit sich bringen. Viel eher sind hier Durchschnittswerte analytisch wertvoll, sowie Maxima und Minima. Da sich die Daten auf Tagesmesswerte beziehen, bedeutet dies z. B., dass der Lufttemperatur–Messwert den Durchschnittswert über den gesamten Tag darstellt. Dagegen bezieht sich der „Lufttemperatur_Maximum“-Messwert auf den Spitzenlufttemperaturwert des gesamten Tages.
Daher kann es aus analytischer Sicht zum einen spannend sein, zu wissen, wie die maximale Tagestemperatur durchschnittlich über einen Monat war, aber auch genauso, welcher maximale Tagestemperaturwert den Spitzenwert im Monat darstellt. Dies gilt ebenso für den Tagesdurchschnittswert der Temperatur. Auch hier sind das Maximum/Minimum sowie der Durchschnitt von Relevanz. Dieser Tatsache werden wir anschließend Rechnung tragen. Zuvor bereiten wir die Fakten-View vor. Zu beachten ist hier, dass fehlerhafte Werte in den Rohdaten als „-999“ eingehen. Diese ersetzen wir mit NULLIF durch NULL-Werte, um die Aggregationswerte nicht zu verfälschen. Die Bewegungsdaten schränken wir zusätzlich auf ab 1. Januar 1900 ein, um die automatische Periodendatenerstellung des Modeler zu nutzen. Die fertige View würde folgendermaßen aussehen:
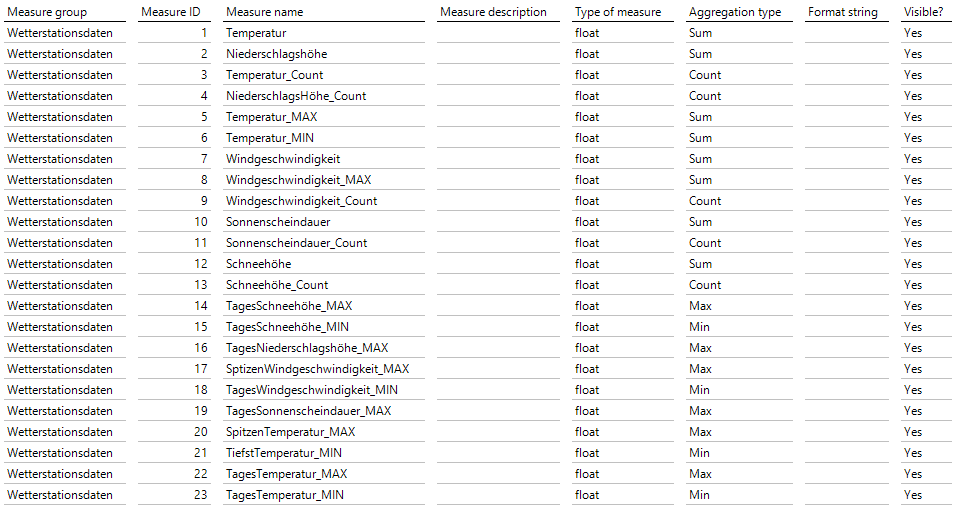
Nachdem wir die Bewegungsdaten nun für die Modellierung vorbereitet haben, können wir die Measuregruppe erstellen und anschließend die Measures selbst definieren. Für die Durchschnittswerte benötigen wir die Kennzahl jeweils vom SUM- und vom COUNT-Aggregationstyp, um die Kennzahl im Frontend erstellen zu können. Bei den Maximum- oder Minimumwerten reicht der jeweilige Aggregationstyp aus.
Analyse
Nachdem wir unser Modell nun fertig modelliert haben, können wir uns ausschnittsweise die daraus hervorgehenden Analysemöglichkeiten betrachten.
Um plastisch aufzuzeigen, was durch die zuvor erläuterte Modellierung nun möglich ist, wollen wir eine Fragestellung als Ausgangspunkt der Analyse formulieren, die viele rein gefühlsmäßig mit einem klaren Ja beantworten würden. Es geht um die Frage, ob es in Deutschland heute im Winter weniger schneit als früher. Um diese Frage beantworten zu können, benötigen wir zuerst die Schneehöhe als Kennzahl. Wir hatten bereits zuvor erläutert, dass in der Betrachtung nur Durchschnittswerte, Maxima oder Minima Sinn machen. Zur Beantwortung der Fragestellung ist hier der Durchschnittwert der richtige Ansatz. Zur Berechnung müssen wir hier nur noch die Division der Schneehöhe als SUM-Aggregationstyp und der Schneehöhe als COUNT-Aggregationstyp durchführen. Mit dem Durchschnittswert können wir nun an die Analyse gehen.
Für eine durch die Fragestellung geforderte zeitliche Betrachtung, nutzen wir die Zeitreihenanalyse. Durch unsere Modellierung können wir die Frage nun sehr präzise beantworten. Denn zum einen können wir auf die in der Frage konkretisierte Jahreszeit eingehen und zum anderen können wir die Frage durch unsere Stationshöhen-Hierarchie auch je Höhenlage beantworten. Damit ist es uns möglich, gleichzeitig noch differenzierter auf die Fragestellung einzugehen.
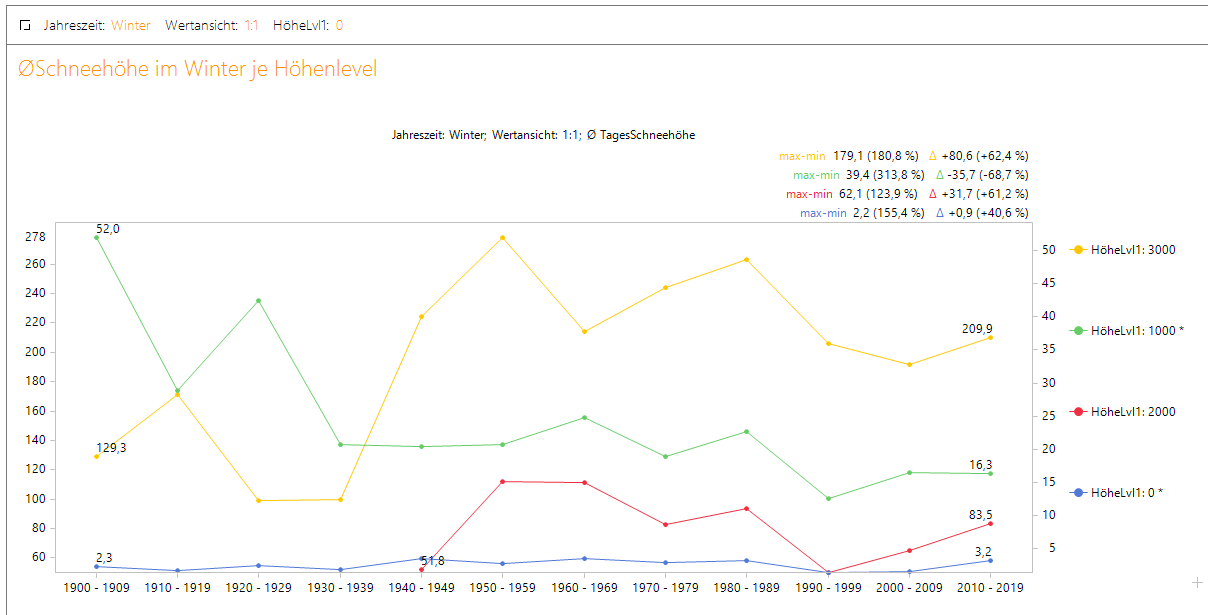
Betrachten wir nun den Bericht, können wir das gefühlte Ja als Antwort aus Datensicht gerade für die höheren Höhenlagen nicht bestätigen. Hier ist das Schneeaufkommen vom Niveau her gleichbleibend bis ansteigend. In den Höhenlagen um 1000 Hm haben wir tendenziell einen Rückgang zu verzeichnen, jedoch ist die Schneehöhe im Flachland (gerundet 0 Hm) konstant bis steigend.
Abbildung 7: Durchschnitts-Schneehöhe
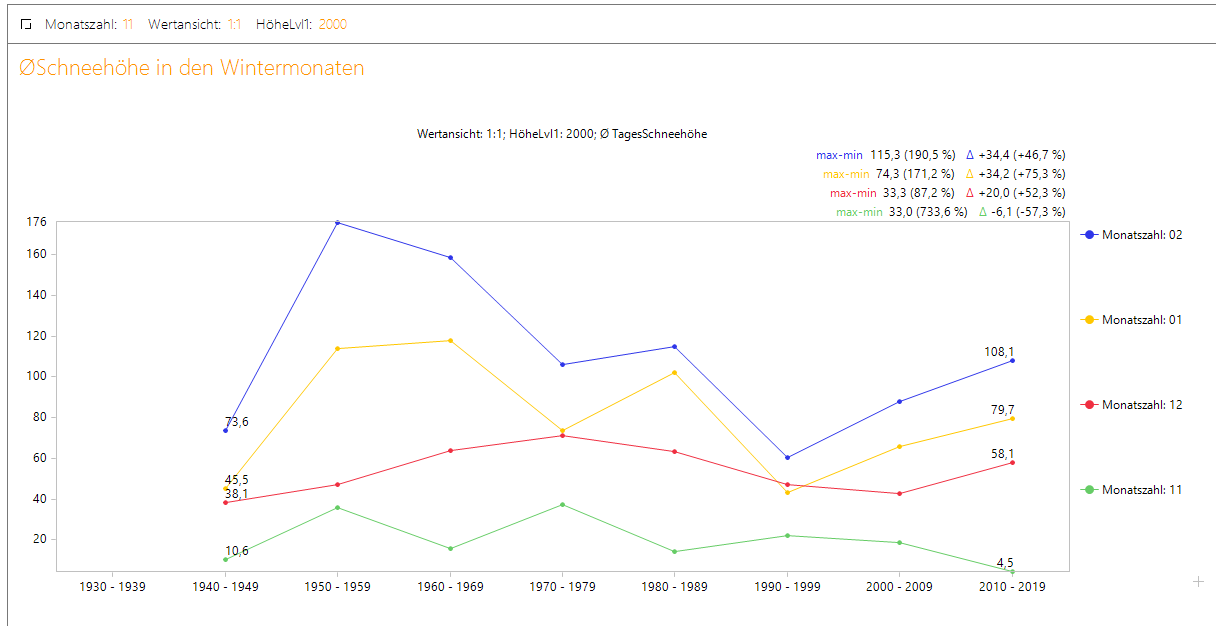
Durch die neue Jahreszeit-Hierarchie haben wir nun sogar die Möglichkeit, die Frage noch genauer zu beantworten, indem wir uns das Schneeaufkommen für die einzelnen Wintermonate betrachten. Was wir hieraus lesen können, ist, dass für die ausgewählte Höhenlage um 2000 Hm zu beobachten ist, dass der November immer ärmer vom Schneeaufkommen wird. Dagegen haben jedoch gerade die Monate Januar und Februar in den letzten Jahrzehnten an durchschnittlicher Schneehöhe zugenommen. Das Schneeaufkommen hat sich demzufolge anscheinend nach hinten verschoben.
Abbildung 8: Durchschnitts-Schneehöhe
Wer Wetterdaten über diesen langen Zeitraum analysieren kann, wird früher oder später auch selbst prüfen wollen, ob die Erderwärmung datentechnisch auch in Deutschland sichtbar ist. Für diese Analyse ziehen wir die durchschnittliche Tagestemperatur heran, die wir auf Jahresebene in einer Rangfolge gegenüberstellen.
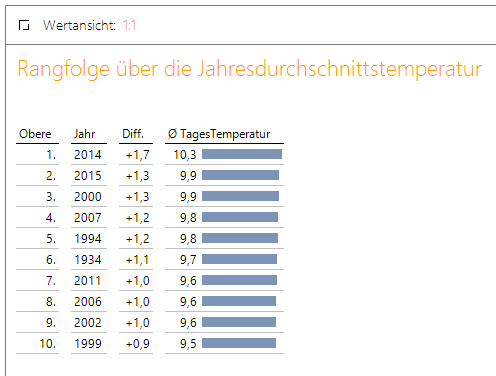
Neben einer Aussage zu den im Jahresdurchschnitt heißesten Jahren über alle verfügbaren Jahre, bekommen wir über die Differenzspalte gleichzeitig noch die positive wie negative Abweichung zum Mittelwert über alle Jahre. Diese kann ebenso als Indikator dienen, wie deutlich der Temperaturanstieg ausgefallen ist. Betrachten wir nun die Rangfolge, lässt sich erkennen, dass sich unter den 10 höchsten Jahresdurchschnittstemperaturen lediglich ein Jahr befindet, dass nicht im Zeitraum der letzten drei Jahrzehnte liegt. Ansonsten stammen alle Jahreswerte aus der näheren Vergangenheit.
Abbildung 9: Rangfolge Jahresdurchschnittstemperatur
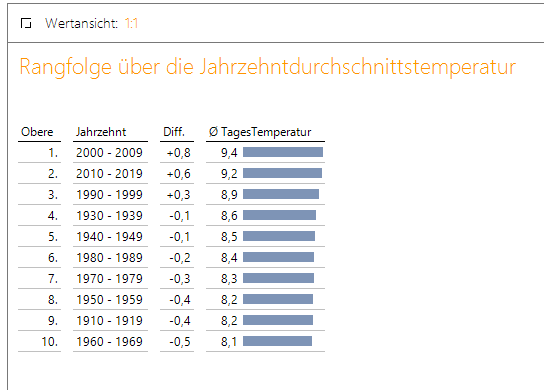
Noch deutlicher wird dies, wenn man sich die Rangfolge nach Jahrzehnten betrachtet. Hier sind die drei letzten Jahrzehnte mit Abstand die wärmsten gewesen. Alle anderen Jahrzehnte liegen unter dem Mittelwert.
Abbildung 10: Rangfolge Jahresdurchschnittstemperatur
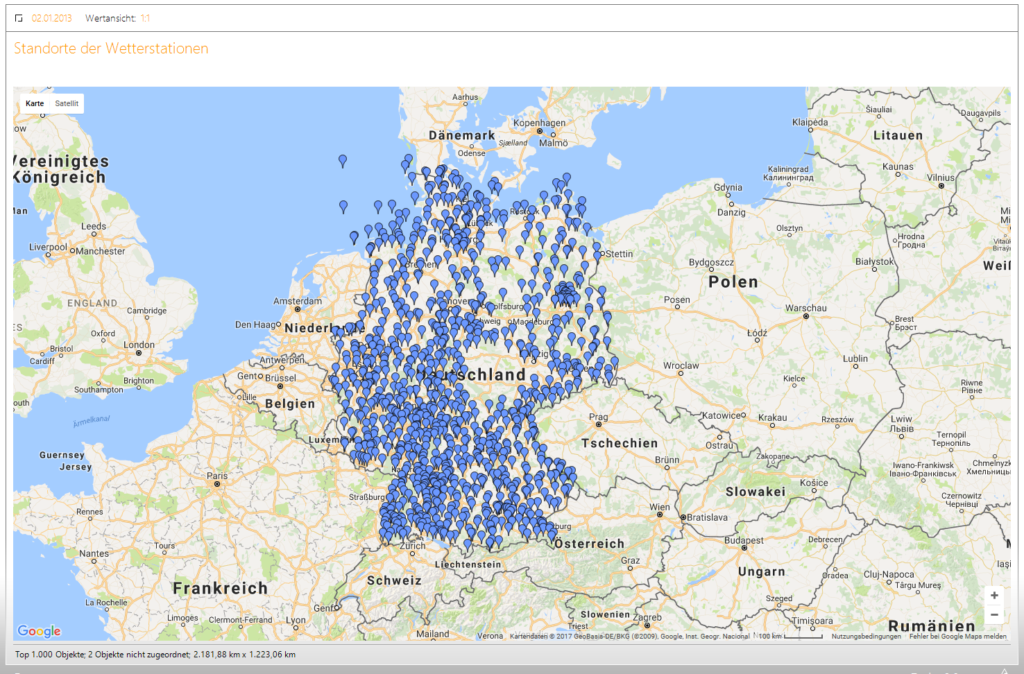
Neben Fragestellungen wie diesen, kann auch ein Blick auf die Standortverteilung der Wetterstationen spannend sein. Durch die Längen- und Breitengrade, die wir mit in das Modell aufgenommen haben, werden auch diese Auswertungen möglich und zeigen uns, wie in diesem Fall, eine interessante Verteilung der Wetterstationen. Hier fällt einem gleich der große leere Fleck auf Höhe des Deutschland-Schriftzuges auf, in dem sich interessanterweise keine einzige Wetterstation befindet.
Abbildung 11: Verteilung der Wetterstationen
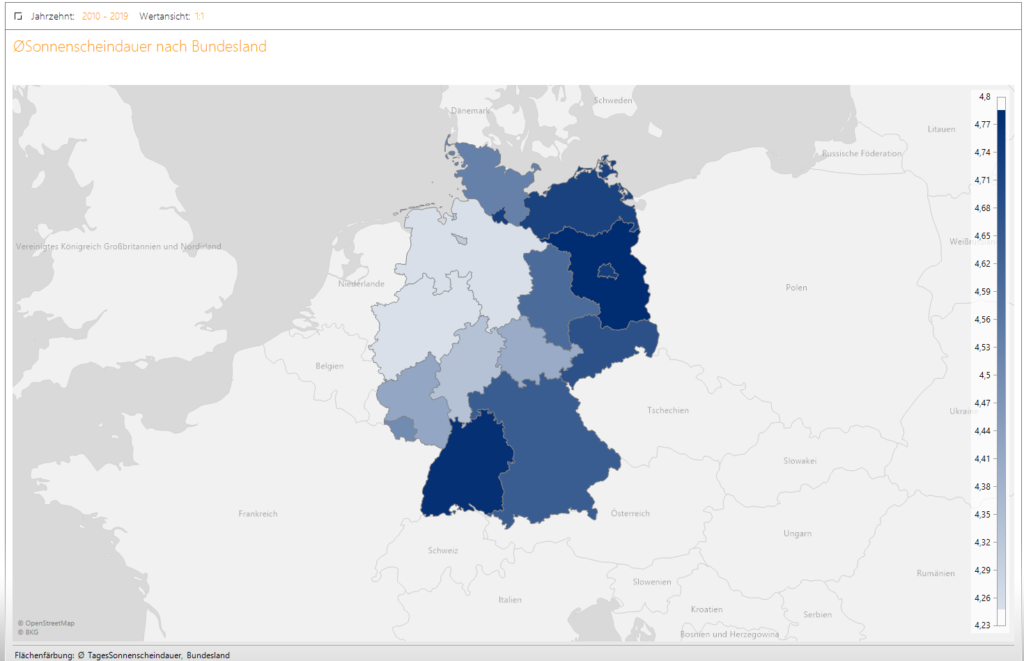
Bei unserer ausschnittsweisen Analyse wollen wir als letztes noch neben der Standortanalyse die zweite Variante der Geo-Analyse, nämlich die der Flächen, betrachten. Neben unserer PLZ-Hierarchie, die wir hier ebenso hätten nutzen können, gibt es zudem die hier genutzte hierarchische Einteilung nach Bundesland. Wir betrachten hier die durchschnittliche Sonnenscheindauer im Jahrzehnt 2010-2019 und können auf einen Blick mit unserer bewährten Farbskalierung erkennen in welchen Bundesländern dieser Wert am höchsten ist.
Abbildung 12: Durchschnittliche Sonnenscheindauer
Diese ausschnittweise Darstellung der Analysemöglichkeiten sollte zeigen, was durch die zuvor erläuterte Modellierungsstrategie in Auszügen alles möglich wird. Ich wünsche viel Spaß beim weiteren Analysieren.