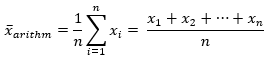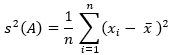Ist es möglich, mit DeltaMaster-Boardmitteln eine XYZ-Analyse durchzuführen? Dieser Blogbeitrag aus der Blogreihe „Auf die Würfel, fertig, los“ beleuchtet die theoretischen Hintergründe dieser Analyse und schildert, welche Überlegungen und Schritte nötig sind, um die gewünschten Aussagen in DeltaMaster zu erhalten.
Was ist eigentlich die XYZ-Analyse ?
Definitionen
Wikipedia
Die XYZ-Analyse ist ein Verfahren der Materialwirtschaft in der Betriebswirtschaftslehre. In dem Verfahren werden […] Güter und Artikel einer Klassifikation bezüglich ihrer Umsatzregelmäßigkeit (Verbrauch und dessen Vorhersagbarkeit) zugeordnet. Dies geschieht meist anhand von Verbrauchsverläufen der Vergangenheit.
Business-on.de
Aus der Materialwirtschaft stammt das Verfahren der XYZ-Analyse. Diese Form der Analyse ist an die ABC-Analyse angelehnt und hilft dabei, Lagerartikel zu klassifizieren. Maßgeblich ist hierbei die Verbrauchsstruktur, Ziel ist die Erstellung einer Prioritätenliste, die die Materialdisposition optimieren soll.
Gruender-Welt.com
Da durch fehlende Materialien Produktionsverzögerungen zustande kommen können (Folge: Fehlmengenkosten), auf der anderen Seite hohe Lagerbestände zu hohen Kapitalbindungskosten führen, ist es sinnvoll optimierte Beschaffungsrhythmen und Bestellsysteme festzulegen. Die Ermittlung des Verbrauchs der für die Produktion notwendigen Güter ist demzufolge eine Grundlage für effizientes Disponieren von Verbrauchsmaterialien und Steuern der Produktionsprozesse. Um die Verbrauchsstruktur bestimmen zu können und entsprechende Bestell-Strukturen zu etablieren, ist die XYZ-Analyse als geeignetes Instrument dafür zu sehen.
Klassifizierung
Dabei werden die Artikel, Güter oder Materialien in die drei Klassen X, Y und Z unterteilt.

Bisweilen wird die XYZ-Analyse auch als RSU-Analyse bezeichnet, mit R für regelmäßig, S für saisonal/trendförmig und U für unregelmäßig.
Nutzen und Ziel
Die XYZ-Analyse ist eine Methode zur Gewichtung des Materials nach der Verbrauchsstruktur, um Aus-sagen über die Vorhersagegenauigkeit machen zu können.
Die Vorhersagegenauigkeit über die Nachfrage nach den Produkten ist wesentlich für die Höhe der vorzuhaltenden Bestände im Rahmen der Vorratspolitik und insb. einer selektiven Lagerhaltung. Je prä-ziser die Produktnachfrage nach Art und Menge im Voraus zu bestimmen ist, desto eher eignet es sich für eine programmorientierte Disposition (Nachfrageschätzung). Verbrauchsgesteuert werden die Teile, die einer stochastischen Nachfrage unterliegen. Die Produktanalyse nach der Prognosesicherheit führt – ähnlich einer ABC-Analyse – zu einer Klassifizierung der Teile in hohe (x), mittlere (y) und niedrige (z) Vorhersagegenauigkeit. Gleichzeitig mit der Vorhersagegenauigkeit ist für eine bestandsarme Distribu-tion (Just-in-Time-Logistik) die Stetigkeit des Verbrauchs und damit die Wiederholhäufigkeit der Nach-frage nach dem Produkt von Bedeutung. Eine hohe Nachfragefrequenz macht es ökonomisch sinnvoll, generelle organisatorische Regeln einzuführen, um so den Informations- und Steuerungsaufwand zu verringern.
Methode
Das xyz-Kriterium wird anhand des Verbrauchsverhaltens des entsprechenden Artikels bestimmt.
Berechnet wird das xyz-Kriterium mithilfe des Mittelwertes des Verbrauches, sowie dessen Standard-abweichung. Den daraus gebildeten Quotienten nennt man Variationskoeffizient.
Die Ermittlung des Variationskoeffizienten über die Standardabweichung erfolgt in vier Schritten:
- Berechnung des arithmetischen Mittels
- Berechnung der Varianz
Die Berechnung der Varianz erfolgt über die Mittelung der summierten Abweichungsquadrate des Mittelwertes. - Berechnung der Standardabweichung
Die Standardabweichung ergibt sich aus der Quadratwurzel der Varianz. - Berechnung des Variationskoeffizienten
Der Variationskoeffizient ergibt sich aus dem Verhältnis der Standardabweichung zum Mittelwert.
Für die Einteilung in die xyz-Klassen werden je nach Quelle verschiedene Grenzwerte des Variations-koeffizienten (VK) angegeben:
Diese Werte stellen somit Richtlinien dar und können im Einzelfall entsprechend angepasst werden.
Auch genügt es nicht, das Schwankungsverhalten der Entnahmemengen je Buchung / Vorgang isoliert zu betrachten, sondern es muss auch das Entnahmeverhalten über die Zeitachse untersucht werden, um eine qualitativ gute Aussage über das Verbrauchsverhalten zu treffen.
Einschränkung und Kritik am Verfahren
Bei der Anwendung der XYZ-Analyse werden auch typische Fehler gemacht, wie etwa die Verwechslung von unregelmäßigem Verbrauch mit chaotischem Verbrauch. Häufig wird schwankender Verbrauch als nicht planbar eingestuft. Wenn jedoch der schwankende Verbrauch z.B. aufgrund saisonaler Bedingun-gen begründet werden kann, ist die Planbarkeit trotzdem gegeben. Schlussendlich ist die kontinuierli-che Überprüfung der getroffenen Maßnahmen ein wichtiger Aspekt.
Damit ist der Variationskoeffizient gut geeignet, um die X-Klasse gegen die beiden anderen Klassen abzugrenzen. Auf der anderen Seite kann der Variationskoeffizient nur eine Krücke sein, um die Y- von der Z-Klasse zu unterscheiden. Wenn man die Werte zufällig permutiert und aus einer schönen Saison-komponente Chaos macht, bleibt der VK identisch.
Praxis
Vorüberlegungen
Welche Kennzahl
Als erstes ist die Kennzahl zu identifizieren, deren Werte im zeitlichen Verlauf betrachtet werden sollen.
In einem Fertigungsbetrieb könnte das zum Beispiel die „Anzahl der verkauften Artikel“ sein, oder in einem Lager die „Anzahl der ausgebuchten Lagerartikel“.
Analyse der Datenreihen unter Berücksichtigung des Datenmodells
Als nächstes müssen die Datensätze unter die Lupe genommen werden, deren Werte man analysieren möchte. Drei Aspekte gilt es zu berücksichtigen, welche maßgebend für die Genauigkeit und die Quali-tät der anschließenden Analyseaussage sind.
- Granularität: Auf welcher Ebene sind die zu analysierenden Datensätze an die Zeitdimension ange-bunden?
- Validität: Wie dicht liegen diese Datenwerte vor?
- Reliabilität: Wie groß ist der Datenraum (mit sinnvollen Daten) im Verhältnis zur angebundenen Zeitebene?
Liegen die zu analysierenden Datensätze mit Zeitstempel vor, kann beliebig nach oben verdichtet wer-den, um Aussagen strategischer Natur zu treffen, aber es bestünde auch die Möglichkeit, das operative Tagesgeschäft zu durchleuchten.
Datensätze auf Tagesebene dürften für die meisten Betrachtungen ideal sein. Sie lassen recht genaue Analyseaussagen zu. Neben der Streuung der Datenwerte kann hier auch die Streuung der Längen der Zeiträume zur Vorgängerbuchung betrachtet werden. Beide Betrachtungen zusammen erlauben ein deutlich präziseres Bild hinsichtlich Planbarkeit, als nur die reine Streuung der Datenwerte.
Beispiel: Fände bei einem Material eine Entnahme von 50 Stück alle 10 Tage statt, so hätte dieses auf Grund der Tatsache, dass die zwischen den Entnahmen liegenden Tage mit 0 (keine Entnahme) bewertet werden müssten, einen Variationskoeffizienten von rund 285%!
Die Betrachtung der zeitlichen Abstände der Entnahmen hätten eine Variationskoeffizienten von 0%. Damit wären die Entnahmen dieses Materials entgegen der Aussage des Variationskoeffizienten auf Basis der Ent-nahmemengen gut disponierbar.
Generell sind auf Datenreihen feinerer Granularität auch präzisere Aussagen möglich.
Trotzdem ist die feinste Granularität nicht immer die beste Wahl. Je feiner die Granularität, desto grö-ßer ist die Menge der Datenzellen in der OLAP Datenbank. Und eine steigende Menge an Datenzellen führt in Abhängigkeit vom restlichen Datenmodell zu sinkender Performance.
Je nach Prozess, aus welchem die Datenreihen stammen, kann es z.B. auf der feineren Tagesebene zu sehr starken Werteschwankungen kommen, welche auf die höhere Monatsebene aggregiert ein viel harmonischeres Bild zeichnen.
Daher ist für gute Analyseaussagen eine ganzheitliche Betrachtung des Szenarios mit seinen Datenrei-hen unerlässlich.
Ein weiterer Faktor bei der Wahl der zeitlichen Ebene, auf welcher der Vergleich der Variationskoeffi-zienten stattfinden soll, ist die Anzahl der Datenwerte pro Datenreihe.
Setzen sich zum Beispiel die Datenreihen zwar aus taggenauen Einträgen, mit aber nur 3-5 Werten über ein ganzes Jahr zusammen, sollte die Analyse der Variationskoeffizienten auf der Ebene der Jahres-summen stattfinden.
Wie dicht die einzelnen Datensätze (je Datenreihe) im betrachteten Zeitraum liegen, hat also einen di-rekten Einfluss auf die Analyse. Idealerweise liegt mindestens ein Wert pro Zeitscheibe je Datenreihe vor.
Da es bei der Analyse um den Vergleich der Datenreihen, beziehungsweise deren Variationskoeffizien-ten geht, ist nachdem die Granularität der Zeitdimension festgelegt wurde ein geeigneter Datenraum zu finden.
Dabei sind Start- und Endperiode dieses Datenraums festzulegen.
Sollen zum Beispiel monatliche Absatzzahlen der Produkte verglichen werden, so sollte ein Startmonat gewählt werden, ab dem auch alle Produkte potenziell zur Verfügung standen. Wird ein Produkt erst im März eingeführt und beworben, so sollte frühestens dieser Monat als Startmonat für den zu analysie-renden Datenraum gewählt werden.
Die Endperiode liegt meist unmittelbar vor der Gegenwart, beziehungsweise auf dem zeitlich letzten im Modell enthaltenen Wert der Datenreihen.
Außerdem muss der Datenraum zeitlich gesehen hinreichend groß sein. Aus einem Datenraum basie-rend auf drei Werten lassen sich kaum gültige Erwartungs- oder Prognosewerte ableiten.
Werden saisonabhängige Datenreihen betrachtet, so sollte sich der Datenraum mindestens über ein Jahr erstrecken und idealerweise sogar noch das Vorjahr umfassen.
Falls möglich, sollte der Datenraum so gewählt werden, dass er äußere Ereignisse, welche sich in den Daten widerspiegeln, ausschließt.
Tipp: Um einen ersten Eindruck der Datenlage zu gewinnen, die Parameter der XYZ-Analyse richtig wählen zu können, und um anschließend die Aussagen der XYZ-Analyse richtig bewerten zu können, ist die Betrachtung der Datenreihen in DeltaMaster mit der Zeitreihenanalyse hervorragend geeignet.
Umsetzung in DeltaMaster
Zur Veranschaulichung werden wir im Folgenden den Variationskoeffizienten am Beispiel der Absatz-werte der Produkte aus der Datenbank Chair Schritt für Schritt herleiten.
Die Absatzwerte liegen in der OLAP Datenbank der Chair aggregiert auf Monatsebene vor. Eine Vorun-tersuchung hat ergeben, dass eine Monatsscheibe pro Produkt bis zu 50 einzelne Absatztransaktionen bündelt. Daher ist der zeitliche Abstand der einzelnen Transaktionen/Verkäufe zueinander nicht rele-vant, ein einzelner Monat ohne eine einzige Absatztransaktion ist aber zwingend mit 0 (kein Absatz) zu bewerten.
Als Startperiode können wir die erste im System vorhandene Monatsscheibe mit Daten wählen. Das wäre im vorliegenden Fall der Jan 2012. Hier tragen 20 von 23 Produkten Datenwerte. Die Produkte, welche in der ersten Monatsscheibe keine Absätze vorweisen können, haben über den gesamten Zeit-raum ohnehin nur sehr geringe Absatzwerte, oder weisen sogar mehrere Absatzmonatslücken auf. Der Datenraum, den wir analysieren werden, kann bis zur letzten im System verfügbaren Monatsscheibe laufen.
Damit auch Vergangenheitsbetrachtungen möglich werden, baue ich die ganze Berechnung dynamisch auf. Das heißt, die Variationskoeffizienten werden abhängig von der jeweiligen Monatsscheibe berechnet.
-
- Monate zählen
Wir legen eine neue MDX-Kennzahl an, welche die Anzahl der im betrachteten Datenraum enthaltenen Monate enthält.count( {[Periode].[Periode].[Monat].&[201201]:[Periode].[Periode].Currentmember} , INCLUDEEMPTY )leere Monate werden mitgezählt (entspricht Bewertung mit Null)
Startperiode hier Jan 2012 - Durchschnittlicher Absatz
Die zweite MDX-Kennzahl baut auf der ersten auf, und ermittelt den durchschnittlichen Absatzwert in Abhängigkeit der jeweiligen Monatsscheibe.
Diese Berechnung lässt sich elegant unter Anwendung eines kleinen Tricks erstellen. Zuerst fügen wir in der Kumulations-Dimension ein Zeitanalyseelement hinzu, welches alle Werte auf die ‚(All)‘-Ebene der Periode miteinander kumuliert. Das heißt, dieses Element enthält die Summe des eigenen Wertes und aller auf derselben Ebene liegenden, zeitlich vorangegangenen Werte.(#1, [Kumulation].[Kumulation].[temp]) / #2#1 stellt den Absatzwert dar
#2 ist der Platzhalter für die Kennzahl aus Schritt 1
[Kumulation].[Kumulation].[temp] ist unser neues Kumulationselement.
Anmerkung: Hätten wir nicht die erste im System enthaltene Monatsperiode als Startperiode des für die Analyse relevanten Datenraums wählen können, müssten wir noch die Absatzwerte ausschließen, welche zeitlich vor der Startperiode liegen. - Abweichung des einzelnen Absatzwertes zum arithmetischen Mittel im Quadrat
Die dritte Kennzahl repräsentiert die Abweichung des jeweiligen Absatzwertes zum Monatsmittel im Quadrat, und stellt einen Teilschritt zur Berechnung der Varianz (siehe oben) dar.(#2 - #1)^2#1 stellt den durchschnittlichen Absatz aus Schritt 2 dar
#2 ist der Absatzwert - Varianz und der Standardabweichung
Da die Standardabweichung nur die Quadratwurzel aus der Varianz darstellt, lassen sich diese beiden bequem in einem Schritt berechnen.( sum( {[Periode].[Periode].[Monat].&[201201]:[Periode].[Periode].CurrentMember} ,#1 ) / #2 )^0.5#1 entspricht der Kennzahl aus Schritt 3
#2 enthält die Anzahl der Monate in dem jeweiligen Zeitraum
In diesem Schritt wird also der Gesamtwert des Intervalls (Startperiode bis zur aktuellen Periode) der quadratischen Abweichungen durch die Anzahl der vergangenen Monate geteilt und anschließend daraus die Wurzel gezogen (vergleiche Berechnung Standardabweichung unter dem Abschnitt „Methode“). - Variationskoeffizient (VK)
Als letzter Schritt wird der Variationskoeffizient berechnet.#1 / #2#1 stellt die im vorherigen Schritt berechnete Standardabweichung dar
#2 steht für den durchschnittlichen Absatz aus Schritt 2
Der Variationskoeffizient lässt sich als Verhältnis von Standardabweichung zum Mittelwert begreifen und stellt somit ein Maß der Schwankungsbreite in % um den Mittelwert dar.
- Monate zählen
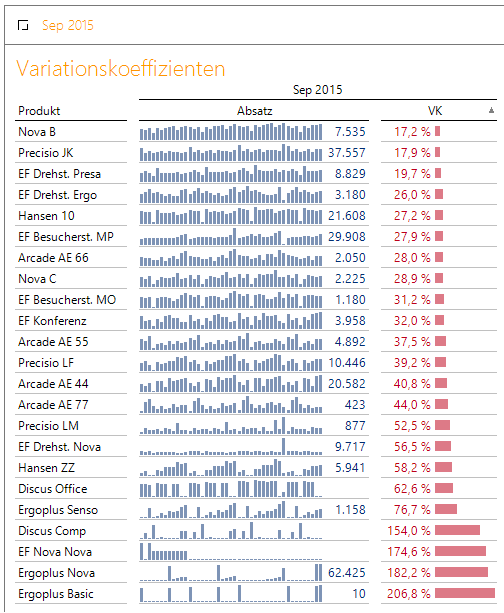
Darstellung mit klassischer DeltaMaster Visualisierung: Die Sparklines bilden den historischen Kontext der Absatzwerte in Relation zum angezeigten Absatz. Spalte zwei zeigt den gerade berechneten, zur Datenreihe gehörigen Variationskoeffizienten VK.
Abbildung 1: DeltaMaster Bericht – Visualisierung der Absatzwerte
Die oberen Produkte bieten hinsichtlich ihres Absatzwertes eine relativ hohe Planungssicherheit. Belegt wird dies durch die geringe Streuung ihrer historischen Werte, welche sich in einem niedrigen Variati-onskoeffizienten niederschlägt.
Bei Betrachtung der Sparklines fallen aber auch die Produkte „Hansen ZZ“ und „Ergoplus Senso“ auf, welche trotz eines relativ hohen Variationskoeffizienten einen regelmäßigen, deterministischen Verlauf aufweisen. Diese beiden wären, unter Berücksichtigung der Saisonkomponente ebenfalls gut planbar.
Quellen
-
- Wikipedia.org
- iBusiness-on.de
- Wirtschaftslexikon24.com
- Standardabweichung.org
- Gruender-welt.com