Bei einer großen Menge von zu untersuchenden Zeitreihen geht der Durchblick schnell verloren. Wir zeigen heute Methoden, mit denen Zeitreihen automatisch gruppiert werden können, sodass eine handhabbare Anzahl von typischen Verläufen entsteht.
Nehmen wir einmal an, dass in einem Unternehmen 100 Produkte hergestellt und verkauft werden, die allesamt unterschiedliche Absatzverläufe über die 52 Wochen eines Jahres aufweisen. In einem einzigen Diagramm abgebildet lassen sich schwerlich Gruppen von typischen Verläufen identifizieren:
100 Absatzverläufe – in dieser Darstellungsform nicht zu analysieren!
Die Verläufe erscheinen sehr unterschiedlich und es kristallisieren sich in dieser Darstellung keine häufiger auftretenden Verläufe heraus.
Wählen wir einmal die ersten vier Zeitreihen zu den Produkten 1 bis 4 aus und zeichnen diese getrennt voneinander:
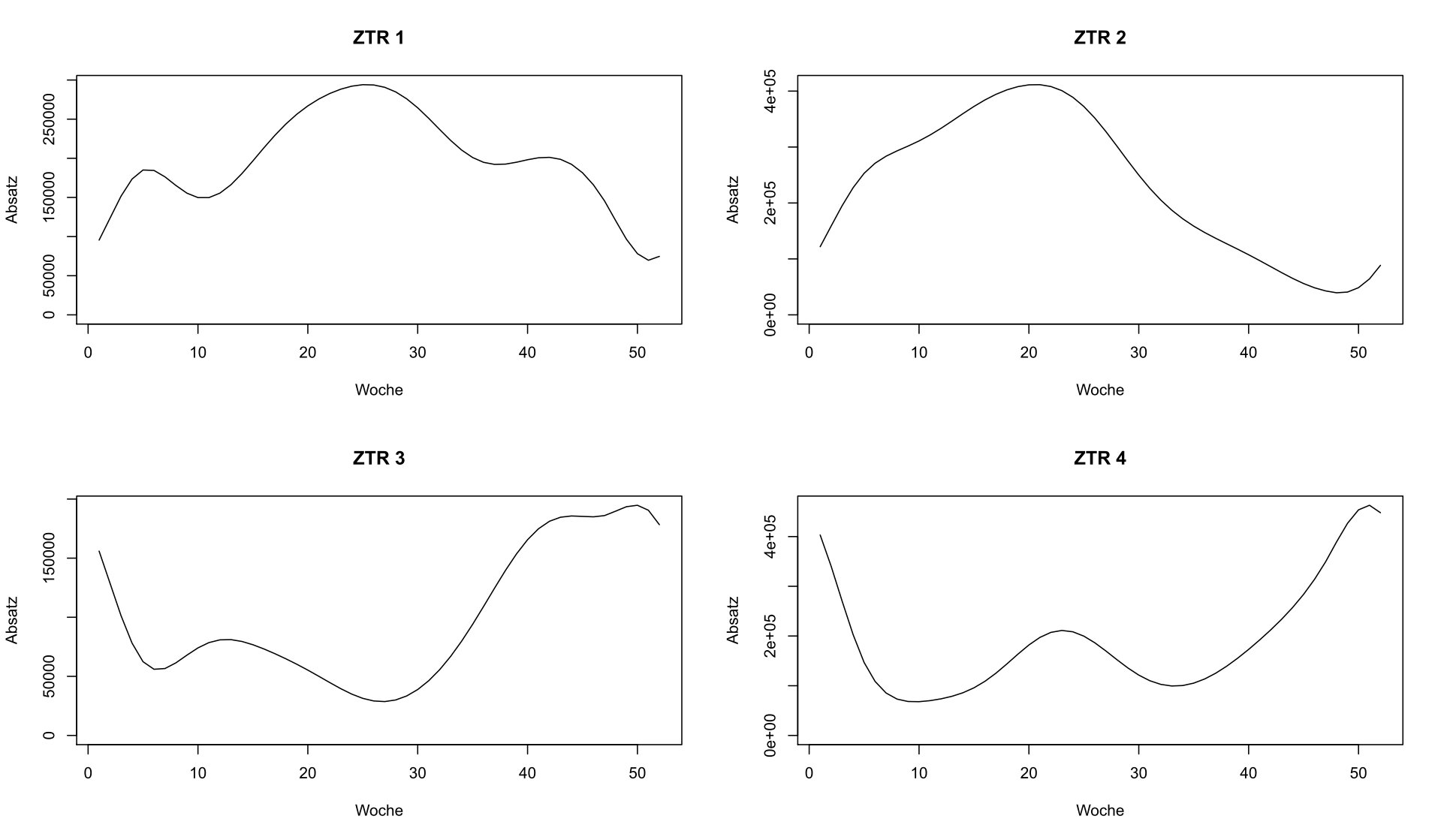
Vier ausgewählte Absatzverläufe
Lautet die Aufgabe, zu ZTR 3 die ähnlichste der anderen drei Zeitreihen zu finden, so legt ein optischer Vergleich ZTR 4 nahe, da beide Zeitreihen zu Jahresbeginn und -ende eher hohe Werte und im restlichen Jahr vergleichsweise niedrige Werte annehmen.
Doch aufgepasst, die Zeitreihen 3 und 4 weisen unterschiedliche Niveaus der Maximalwerte auf – es sind knapp 200.000 bei ZTR 3 und ca. 500.000 bei ZTR. Soll das absolute Niveau eine Rolle spielen oder nicht?
Bevor etwaige Transformationen der Daten in Betracht gezogen werden, sollte jedoch zunächst entschieden werden, ob die Ähnlichkeit überhaupt direkt von den Rohdaten abgeleitet werden soll.
Beispielweise wäre es möglich, eine Zeitreihe mittels Fourieranalyse als Linearkombination gleichförmiger Sinus-Schwingungen unterschiedlicher Frequenzen auszudrücken. Zwei Zeitreihen könnten als ähnlich bezeichnet werden, wenn die höchsten Gewichte bei den gleichen Frequenzen auftreten.
Andere Methoden passen zunächst Modelle an, etwa ARMA(p, q)-Modelle, und die Ähnlichkeit zweier Zeitreihen könnte über die angepassten Parameter definiert werden.
Dieses Vorgehen vereinfacht erstens den Raum, in dem agiert wird. Anstatt mit 52-dimensionalen Vektoren zu hantieren, bräuchte man nun nur noch (p + q) – dimensionale Parametervektoren, mit einer Summe p + q, die normalerweise viel kleiner als 52 ist.
Weiterhin können hierbei zwei Zeitreihen, die tatsächlich mit dem gleichen Modell erzeugt wurden und somit als ähnlich betrachtet werden, trotzdem sehr unterschiedlich aussehen. Es werden somit eher Generierungsmechanismen verglichen und weniger konkrete Realisationen.
Wir bleiben bei den Rohdaten.
Da es uns nur auf die relative Gestalt einer Zeitreihe ankommt, dividieren wir jede Zeitreihe durch ihr Maximum. Die entstehenden Zeitreihen sehen so aus wie bisher, bloß die unterschiedlichen Skalen sind nun durch eine einzige gemeinsame Skala ersetzt worden:
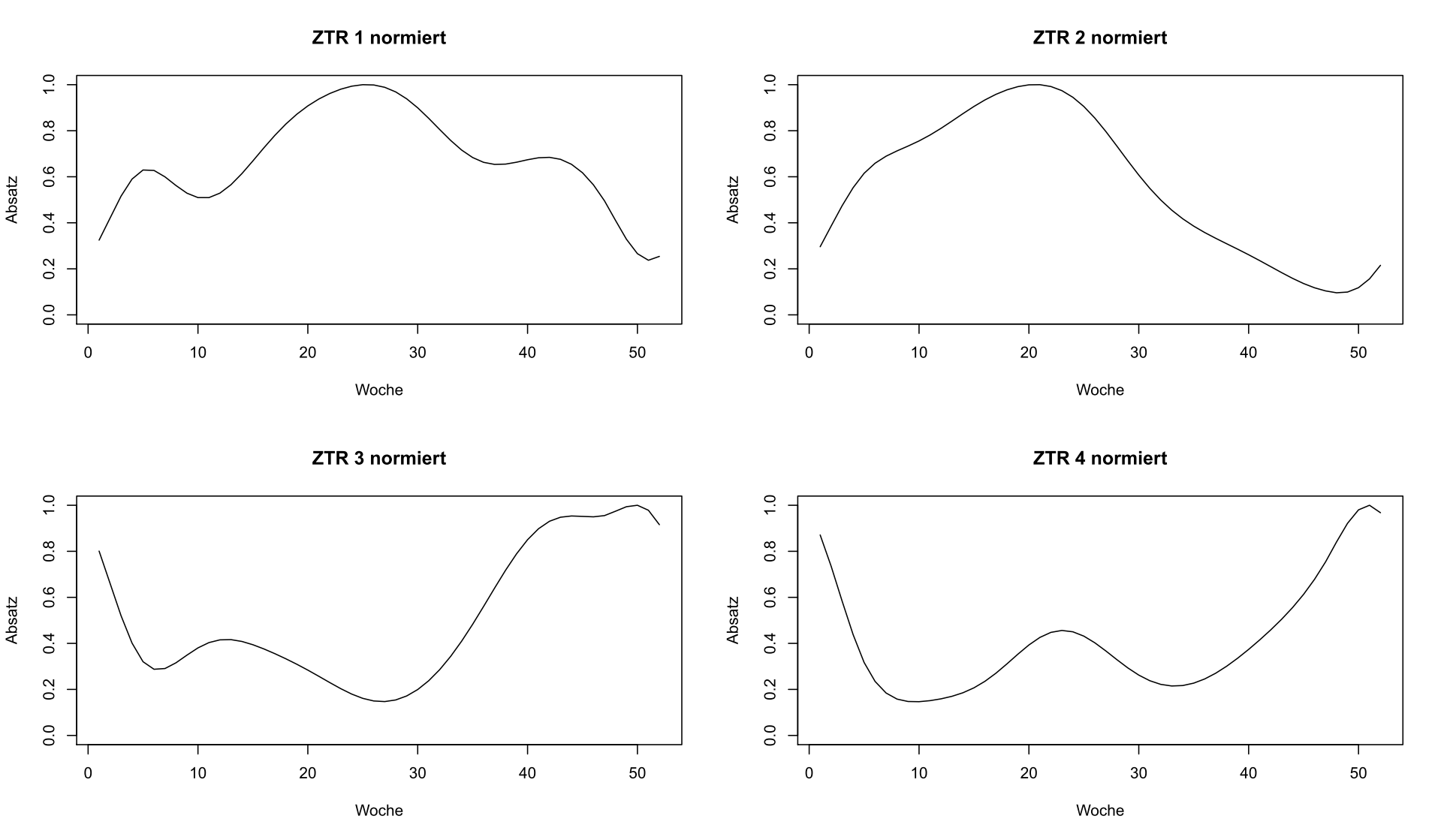
Vier ausgewählte Absatzverläufe – nun normiert!
Um die 100 Zeitreihen clustern zu können, benötigen wir ein Ähnlichkeitsmaß. Das einfachste behandelt jede Zeitreihe als 52-dimensionalen Vektor und misst den euklidischen Abstand zwischen zwei Zeitreihen, respektive Vektoren. Das heißt übrigens auch, dass die Reihenfolge der Zeitpunkte keine Rolle spielt. Vertauscht man etwa für jede Zeitreihe die Werte der Zeitpunkte 7 und 41, so bleiben die Abstände zwischen den Zeitreihen völlig unverändert.
Berechnet man die Abstände zwischen alle möglichen Paaren, ergibt sich eine Abstandsmatrix, die als Grundlage von Clusterverfahren verwendet werden kann. Hier versuchen wir es mit einer agglomerativen Variante, die ausgehend von 100 „Ein-Element-Clustern“ sukzessiv ähnliche Cluster zusammenlegt, bis die (willkürlich gewählte!) Anzahl von 9 Clustern erreicht ist. Schauen wir einmal auf die folgende Grafik, die die Zeitreihen der 9 Cluster darstellt:
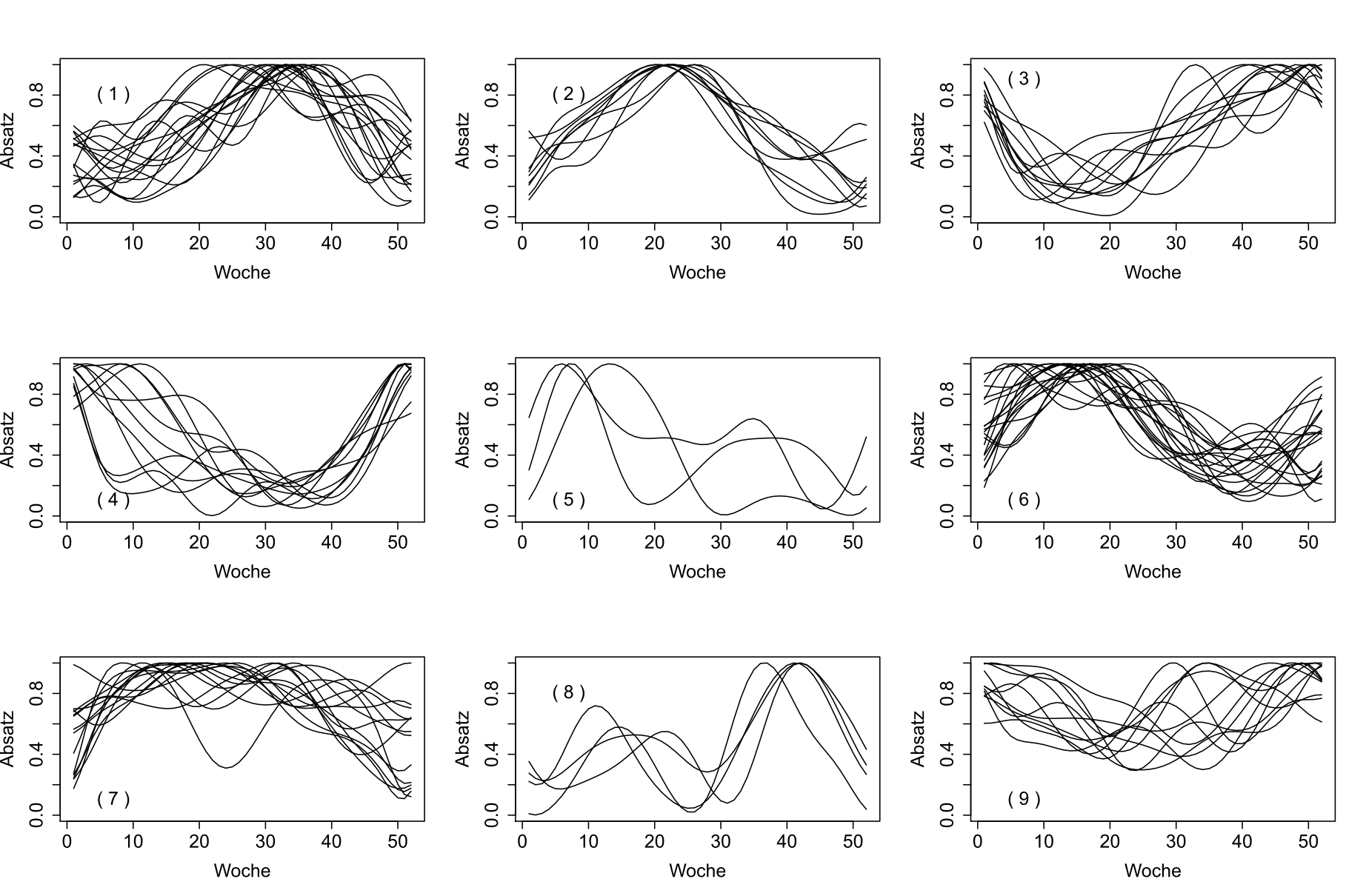
9 Cluster mit den zugeordneten Zeitreihen
Hier wurde die Zuordnung einer Zeitreihe zu einem Cluster erzwungen, man hätte alternativ für die Fälle, die zu gar keinem der 9 Cluster passen wollen, einen eigenen Restecluster aufmachen können.
Cluster 2 passt zu Zeitreihen mit hohen Werten in der Jahresmitte und niedrigen an den Rändern. Cluster 6 nimmt das Maximum eher in der ersten Jahreshälfte an, Cluster 1 eher in der zweiten. Die Verläufe von zwei Zeitreihen aus Cluster 1 und 6 werden wegen der verwendeten euklidischen Distanz doch als recht unterschiedlich angesehen.
Wir wollen jetzt einen Blick auf eine weitere Möglichkeit werfen, eine Ähnlichkeit zwischen zwei Zeitreihen zu definieren. Die Dynamische Zeitnormierung – wir verwenden hier lieber das eher gebräuchliche englische „Dynamic-Time-Warping“ – erlaubt es zumindest zum Teil, auch qualitative Ähnlichkeiten zu berücksichtigen.
Schauen wir noch einmal auf die Zeitreihen zu den bereits erwähnten Produkten 3 und 4, die in der folgenden Abbildung in der oberen Hälfte dargestellt sind – x entspricht ZTR 3 und y ZTR 4 (klicken Sie bitte auf die Grafik für eine vergrößerte Darstellung). Stellen wir uns einmal vor, dass die Zeit elastisch sei und sowohl gestreckt, als auch gestaucht werden könnte.
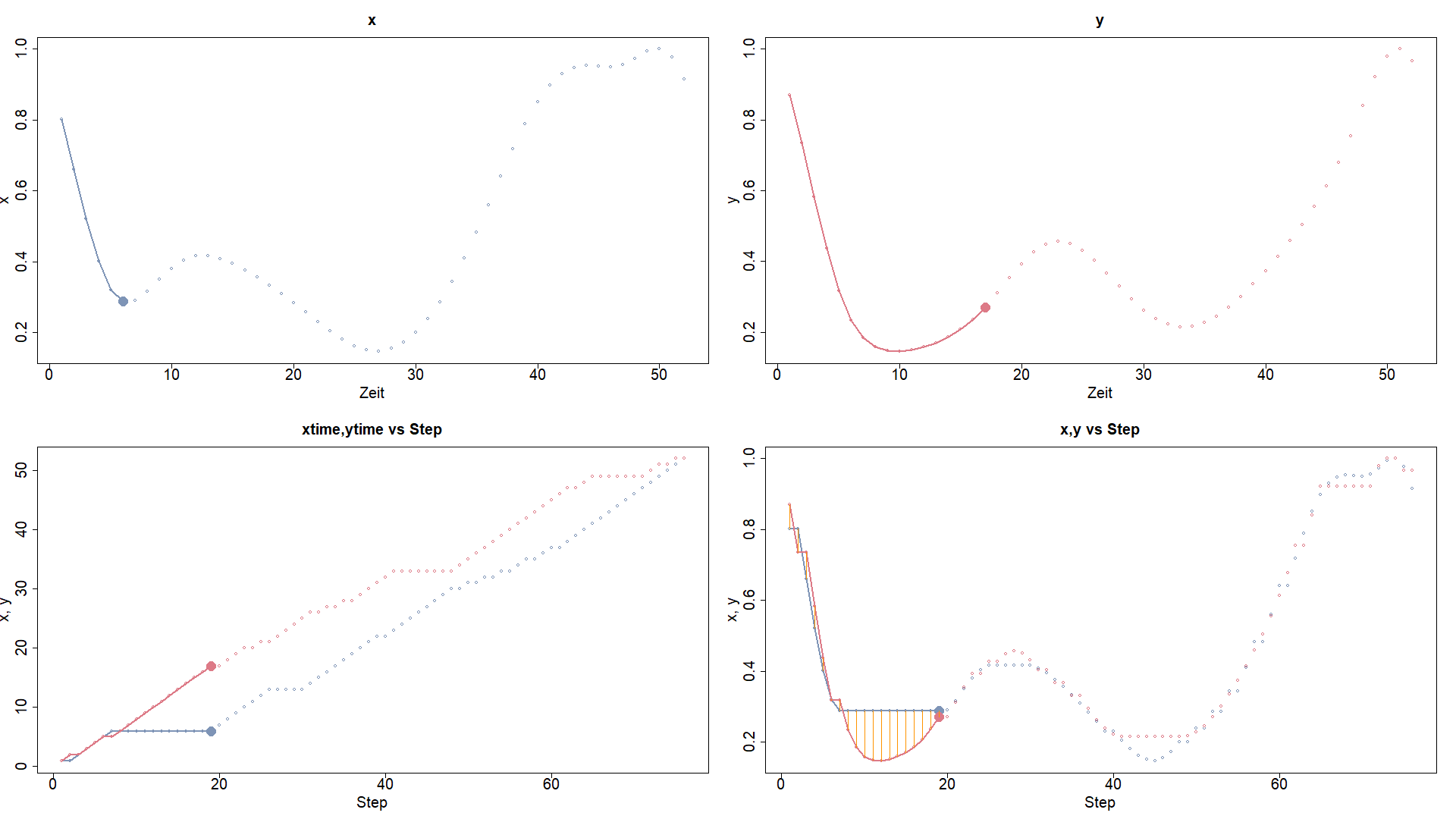
Dynamic-Time-Warping in der Anwendung
Könnte die Zeit links langsamer ablaufen, sodass das erste Minimum von x nicht bei t = 6, sondern bei t = 10, das erste lokale Maximum nicht bei 13, sondern bei t = 23 und das zweite lokale Minimum nicht bei t = 27, sondern bei t = 34 aufträten, wären die entstehenden Kurven viel ähnlicher.
Zur Berechnung eines Abstandsmaßes stelle man sich vor, dass anfangs beide Zeitreihen auf ihrem ersten Wert bei t = 1 stehen. In jeder Runde darf man nun in jeder Zeitreihe entweder einen Schritt vorrücken oder nicht. Wenn beide Zeitreihen simultan vorrücken, entsteht keine zeitliche Verzerrung. Rückt beispielsweise nur y einen Schritt vor, steht für x die Zeit still.
Beide Zeitreihen müssen am Ende der Prozedur auf ihrem Endwert (hier t = 52) stehen.
Die Teilabbildung links unten zeigt, ob eine Zeitreihe vorrückt (Steigung von 45 Grad) oder ob die Zeit stehen bleibt (waagerechtes Teilstück). Die Abbildung rechts unten zeigt die momentanen, zugeordneten Zeitreihenwerte jeder Runde und schraffiert dargestellt die Abweichung, die in der gewichteten Summe möglichst klein sein soll (Details der exakten Berechnung der Summe lassen wir hier einmal weg!).
Wir möchten nun beide Zeitreihen so vorrücken lassen, dass die zu jedem Teilschritt entstehenden Zeitreihenwerte möglichst ähnlich sind.
Mittels Methoden der Dynamischen Programmierung lässt sich ein optimales Vorgehen ermitteln, das wir beim hier gezeigten Beispiel bereits angewendet haben. Hier in unserer Grafik hat x (ZTR 3) gerade 13 Perioden ausgesetzt, um y (ZTR 4) das Fortschreiten zu ermöglichen. In der Folge werden beide Zeitreihen den Anstieg zu ihrem lokalen Maximum nahezu synchron angehen.
Das folgende kurze Video illustriert noch einmal die Schritte, bis beide Zeitreihen ihr jeweiliges Ende erreicht haben. Schauen Sie es sich ein paar Mal an und konzentrieren Sie sich am besten immer auf eine Teilabbildung:
Sie sehen gerade einen Platzhalterinhalt von YouTube. Um auf den eigentlichen Inhalt zuzugreifen, klicken Sie auf die Schaltfläche unten. Bitte beachten Sie, dass dabei Daten an Drittanbieter weitergegeben werden.
Übrigens ließen sich so auch Zeitreihen unterschiedlicher Länge vergleichen. Als Ergebnis erhalten wir einen Abstand, der aus den schraffiert dargestellten Differenzen der Teilabbildung rechts unten berechnet wird.
Wenn zwei Zeitreihen nur zeitlich versetzt sind, etwa mit einem Lag von beispielsweise drei Wochen, aber ansonsten identisch aussehen, so wird die Ähnlichkeit trotzdem sehr hoch sein!
Die vorauseilende Zeitreihe setzt anfangs drei Runden aus, aber dann können beide Zeitreihen im Gleichschritt vorwärts marschieren und weisen dabei keine Abweichungen auf. Zum Schluss macht dann die vorauseilende Zeitreihe noch drei Schritte, während der Nachzügler auf seinem letzten Wert verharrt.
Wir vergleichen wieder jede Zeitreihe mit jeder und wenden dann das bereits oben eingesetzte agglomerative Clusterverfahren an, wieder mit der willkürlich gewählten Anzahl von 9 Clustern. Wie sehen hier Zeitreihen aus, die als ähnlich klassifiziert wurden?
Da ja die Zeitachse verzerrt sein kann, wenn Dynamic-Time-Warping betrieben wird, ist es nicht besonders clever, alle Zeitreihen eines Clusters übereinander zu zeichnen, wie es bei der euklidischen Distanz der Fall war.
Wir zeigen deshalb alternativ 5 Beispielzeitreihen pro Cluster (bzw. 2 für den Cluster ganz rechts), die hier spaltenweise angeordnet sind:
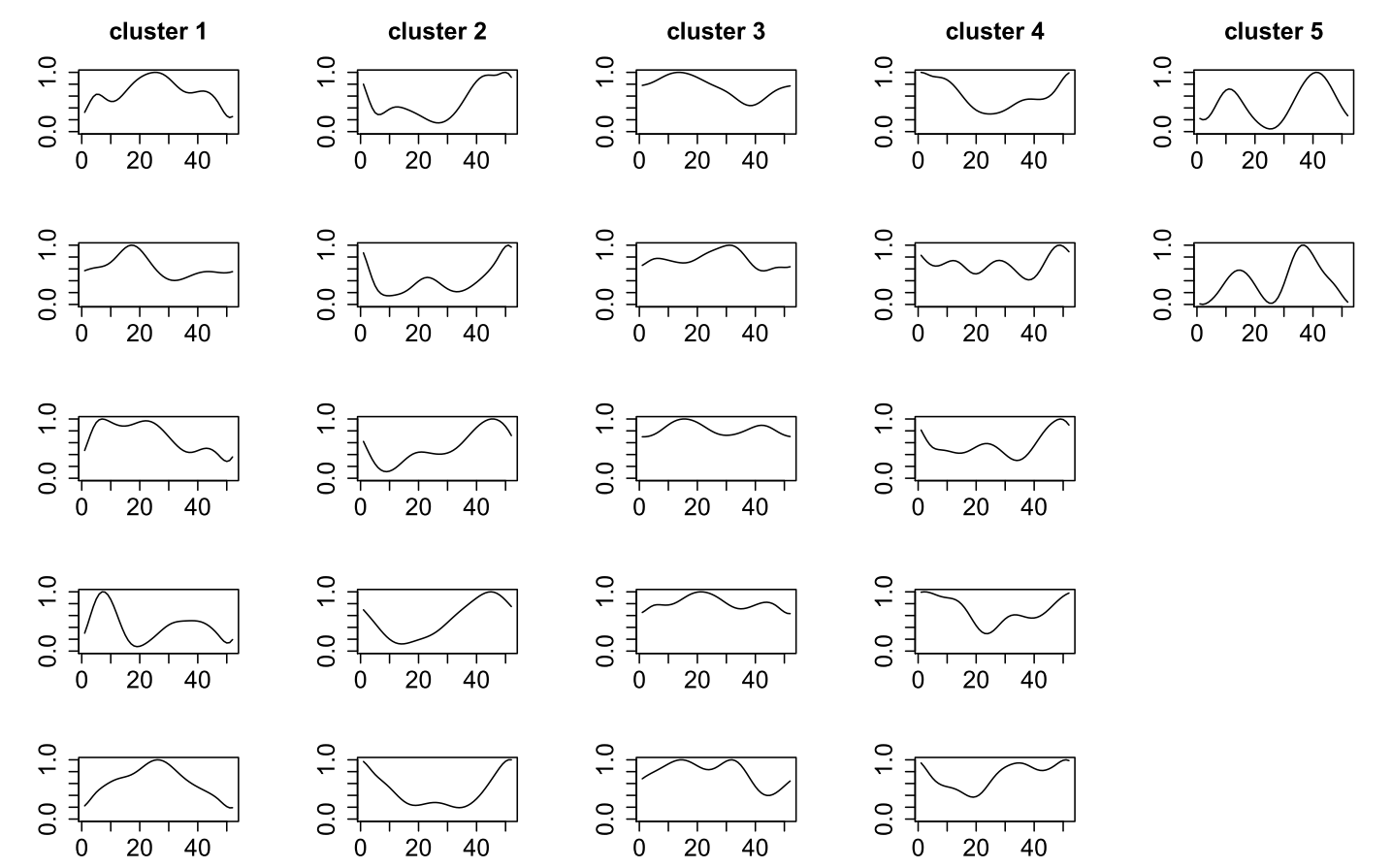
Jeweils 5 Beispiel-Zeitreihen pro Cluster
Die Interpretation stammt nun natürlich aus der ex-post-Betrachtung der zugeordneten Zeitreihen. Zeitreihen aus Cluster 1 beginnen tief und enden tief. Die Zeitreihen aus Cluster 2 beginnen hoch und enden hoch. Zeitreihen aus Cluster 4 sehen ähnlich aus, sinken aber nicht so tief.
Die Beispiele aus Cluster 3 halten sich eher im oberen Drittel auf und weisen auch zumeist 2 lokale Maxima auf.
Die beiden Beispiele aus Cluster 5 starten und enden tief und besitzen zwischendurch 2 lokale Maxima, ein niedriges und ein hohes.
Die folgende Abbildung zeigt einmal das ähnlichste Zeitreihenpaar bei der euklidischen Distanz (oben) und bei der Verwendung von Dynamic-Time-Warping (unten):
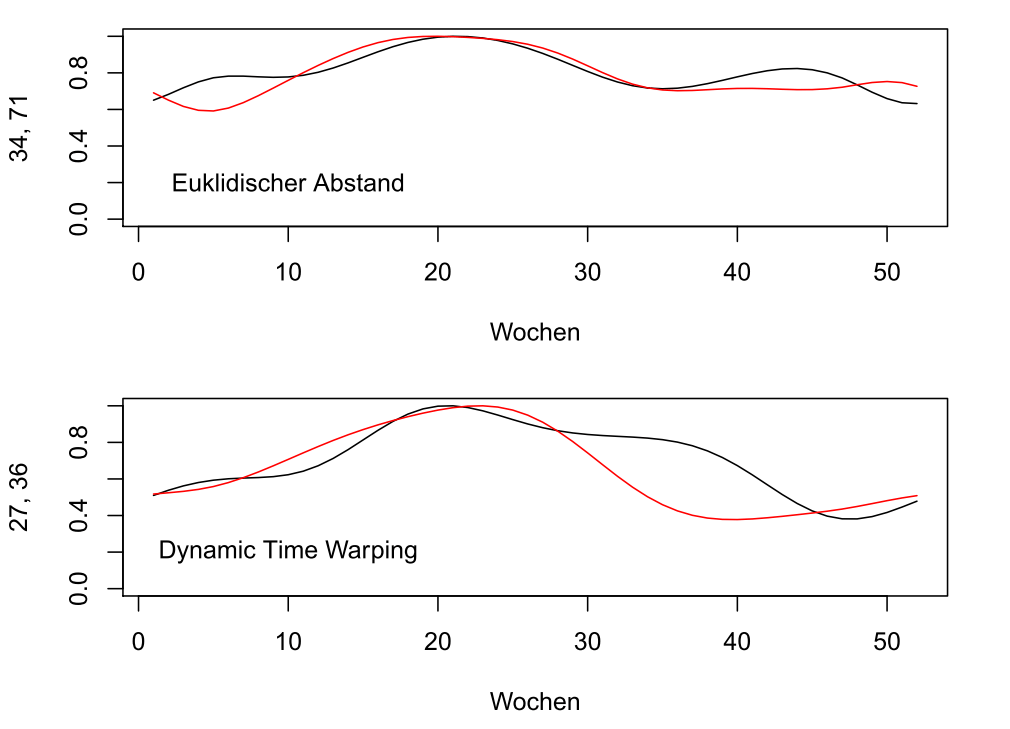
Die ähnlichsten Zeitreihenpaare bei euklidischer Distanz (oben) und bei Dynamic-Time-Warping (unten)
Dass die beiden Zeitreihen im Falle des Dynamic-Time-Warping trotz des großen Abstandes zwischen den Zeitpunkten 30 und 45 als ähnlich angesehen werden, kann mit drei Eigenschaften begründet werden:
- Beide Zeitreihen beginnen und enden auf einem ähnlichen Level
- Beide Zeitreihen haben nur ein lokales Maximum mit identischem Wert 1
- Beide Zeitreihen haben ein lokales Minimum rechts vom Maximum auf identischer Höhe
Speziell die letzte Eigenschaft sichert die Existenz einer zeitlichen Verzerrung, die beide Zeitreihen nahezu zur Deckung bringt:
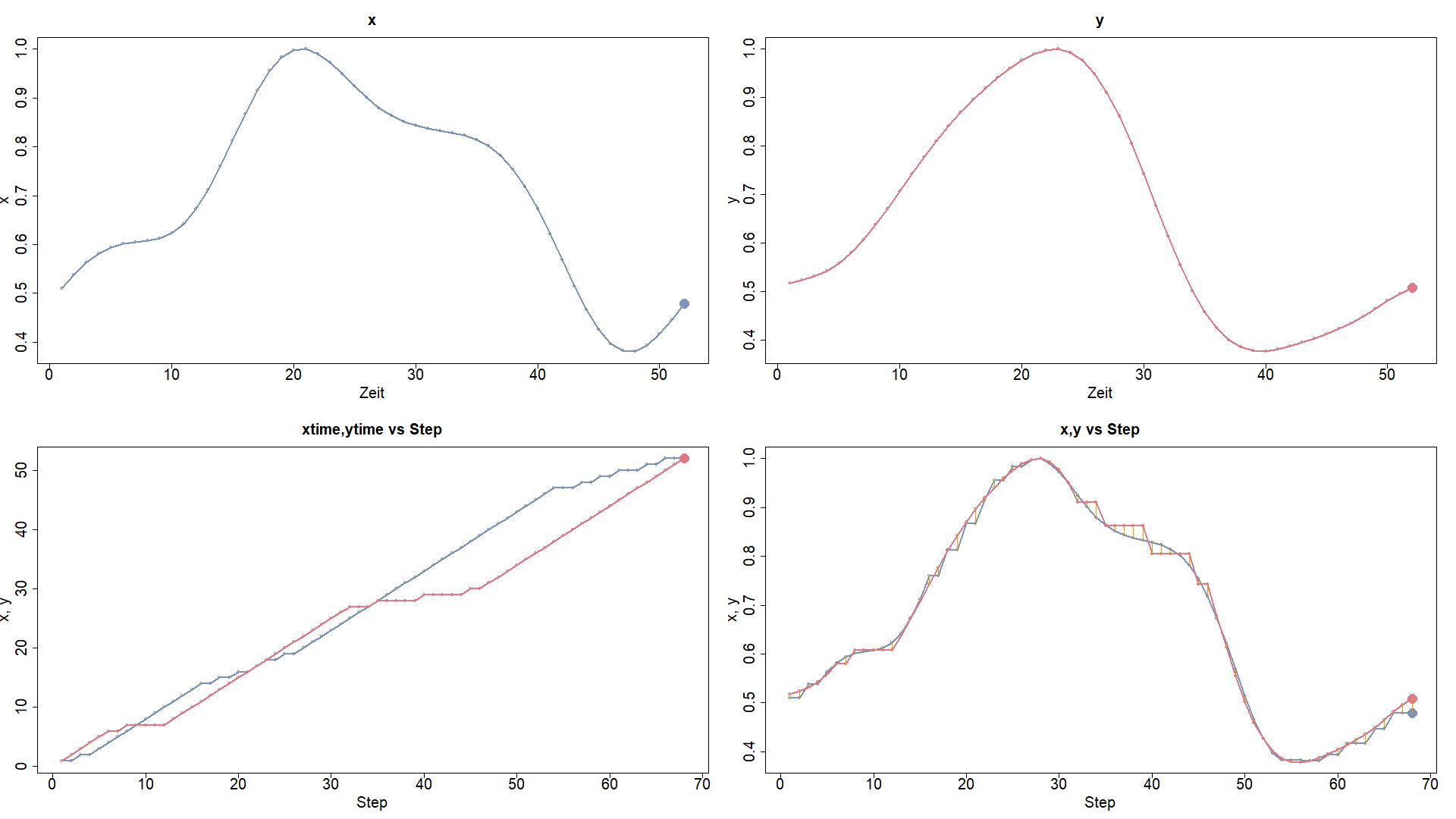
Dynamic-Time-Warping in Vollendung
Es existiert eine Vielzahl von möglichen Methoden, Ähnlichkeiten zwischen Zeitreihen zu definieren. Die Dynamic-Time-Warping-Methode ist nur eine davon, hat aber unter anderem den Vorteil, auch auf Zeitreihen unterschiedlicher Länge anwendbar zu sein.
Hier haben wir „unsupervised“ gearbeitet und die Cluster selbst generiert. Sind mögliche typische Verläufe bekannt, könnte man Prototypen definieren und über die Ähnlichkeit zu den Prototypen Klassifikation betreiben.
