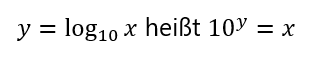Stetig werden Daten gesammelt und veröffentlicht. Bevor wir uns zu vertrauensselig auf ihre Korrektheit verlassen, sollten wir lieber die Datenintegrität prüfen. In bestimmten Fällen greift dann eine verblüffende Methode, mit der manche Manipulation zielsicher erkannt wird!

Kann man veröffentlichten Daten ansehen, ob sie manipuliert worden sind? Man kann – zumindest in ausgewählten Fällen!

Das Verfahren, das wir in diesem Blogbeitrag vorstellen wollen, basiert auf einer paradox erscheinenden Beobachtung. Zur Illustration schauen wir uns einmal einen unverfänglichen Datensatz an. Bei diesem geht es um die integrierten Schulden der Gemeinden und Gemeindeverbände Bayerns am Ende des Jahres 2012 (*):

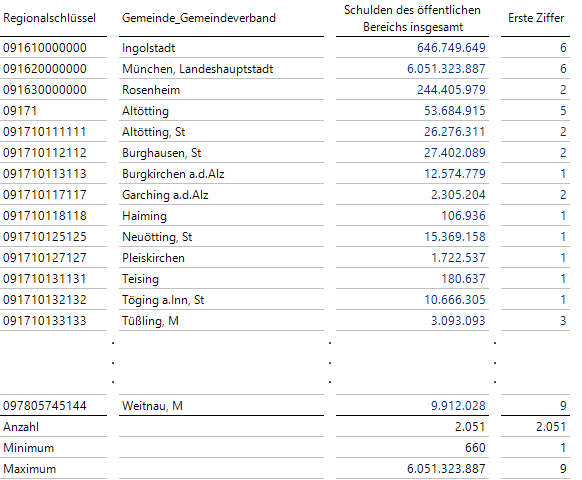
Schulden der Gemeinden Bayerns (Stand 31.12.2012)

Die Gemeinden ohne Schulden sind in der Tabelle nicht mehr enthalten.

Schauen wir auf die aggregierten Werte am Ende dieser für die Abbildung stark gekürzten Tabelle, sehen wir die recht hohe Zahl von Gemeinden (n = 2051), deren Schuldenbeträge sehr stark von nur 660 € bis zu stattlichen 6 Milliarden € variieren.

Wie sollte man nun als verwaltungstechnisch unbeschriebenes Blatt etwaige Ungereimtheiten bei den Daten erkennen können, ohne überhaupt Detailwissen über irgendeine der Gemeinden zu besitzen? Dazu schauen wir auf die führende Ziffer der Schuldenbeträge (siehe letzte Spalte der Tabelle!) und zählen Häufigkeiten!

Halten wir kurz inne und schätzen doch einmal, wie häufig die Ziffern von 1 bis 9 (0 ist keine führende Ziffer) wohl vorkommen werden.

Eine naive Sicht wähnt alle Ziffern gleich häufig, und es sollten bei 2051 Beobachtungen ca. 2051/9 ~ 228 Fälle pro Ziffer vorkommen. Schauen wir nun auf die tatsächlichen Anzahlen, erleben wir eine Überraschung:

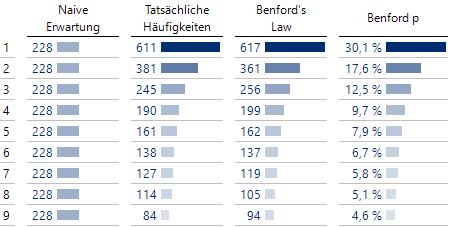
Überraschung bei Naivität, keine bei Kenntnis des Benfordschen Gesetzes

Die 1 kommt als führende Ziffer viel häufiger vor als andere Ziffern: In 611 Gemeinden, das sind ca. 30 % aller Fälle, beginnt der Schuldenbetrag mit einer Eins. Dieses Beispiel ist keine Ausnahme; es sind bereits sehr häufig Konstellationen gefunden worden, bei denen eine solche schiefe Verteilung auftreten kann.

Es kommt noch besser: Das Benfordsche Gesetz (Benford’s Law, das nach dem eigentlichen Entdecker eher Newcomb‘s Law heißen müsste!) sagt die Häufigkeiten sogar quantitativ sehr gut vorher. In der obigen Tabelle zeigt die 4. Spalte die Wahrscheinlichkeiten gemäß diesem Gesetz und die daraus abgeleiteten erwarteten Häufigkeiten für n = 2051 in der 3. Spalte.

Diese erwarteten Häufigkeiten liegen dermaßen dicht an den tatsächlichen Werten, dass ein Chi-Quadrat-Test einen hohen p-Wert von 0.826 erzielt, also überhaupt keine Auffälligkeiten entdeckt. Das heißt, bei diesen Daten deutet nichts daraufhin, dass an den Werten manipuliert wurde.

Es stellen sich somit zwei Fragen: Wann gilt das Benfordsche Gesetz und welche Arten von Manipulationen können entdeckt werden?

Dass das Benfordsche Gesetz kein allgemeingültiges Naturgesetz ist, sehe ich an folgendem einfachen Beispiel: Wenn ich meine täglichen Zimmertemperaturen festhalte, werde ich wohl zwar auch meistens eine 1 als erste Ziffer erhalten, etwas seltener eine 2 (im Office gilt bereits die umgekehrte Konstellation) und ganz selten eine 3, aber die anderen Ziffern dürften zumindest in näherer Zukunft nicht an führender Stelle vorkommen. Hier ist das Benfordsche Gesetz also schon einmal nicht anwendbar.

Ein anderes Beispiel ist durch den Regionalschlüssel aus der obigen Tabelle gegeben, der bei allen Gemeinden mit einer 9 als führende Ziffer vertreten ist.

Schauen wir uns eine mögliche Formulierung des Benfordschen Gesetzes einmal genauer an; der 10er-Logarithmus wird dabei eine wichtige Rolle spielen.

Zunächst stellt man fest, dass eine Multiplikation oder Division einer Zahl mit 10 nicht die führende Ziffer ändert. Wir können also getrost alle Werte durch eine passende 10er-Potenz dividieren, sodass Zahlen aus dem Intervall [ 1 ; 10) entstehen. Nehme ich von einer solchen Zahl den 10er-Logarithmus, so entsteht ein Wert aus dem Intervall [0 ; 1). Zur Erinnerung sei hier noch einmal die Definition des 10er-Logarithmus genannt:

Bei unserem Schuldenbeispiel ergeben sich die folgenden Berechnungsschritte

Berechnung der 10er-Logarithmen

Die vorletzte Spalte zeigt die normierten Schuldenwerte, die nun im Intervall [ 1 ; 10) liegen, ohne dass die führende Ziffer verändert wurde. Der 10er-Logarithmus einer solchen Zahl liegt dann im Intervall [ 0 ; 1). 10 hoch die letzte Spalte ergibt somit die vorletzte Spalte.

Das Benfordsche Gesetz gilt nun dann, wenn angenommen werden kann, dass die Zahlen der letzten Spalte auf dem Intervall [ 0 ; 1) gleichverteilt sind.

Möchte man wissen, welche Zahlen der letzten Spalte zu einer 1 als führende Ziffer in der vorletzten Spalte führen, muss man nur berücksichtigen, dass eine Zahl x mit 0 <= x < log10(2) mittels der Operation y = 10^x zu einem Wert y aus dem Intervall [ 1 ; 2) führt und sich somit die 1 als führende Ziffer ergibt.

Die Wahrscheinlichkeit dafür ist wegen der angenommenen Gleichverteilung durch log10(2) ~ 0.30103 gegeben.

Analog kann man zeigen, dass allgemein die führende Ziffer i mit Wahrscheinlichkeit p(i) = log10(i+1) – log10(i) auftritt und sich die Benford-Werte p aus der oben erwähnten Häufigkeitstabelle ergeben.

Dass die Annahme gleichverteilter Werte bei unserem Schuldenbeispiel nicht zu weit hergeholt ist, zeigt ein Histogramm der 2051 10er-Logarithmen aus der letzten Spalte.

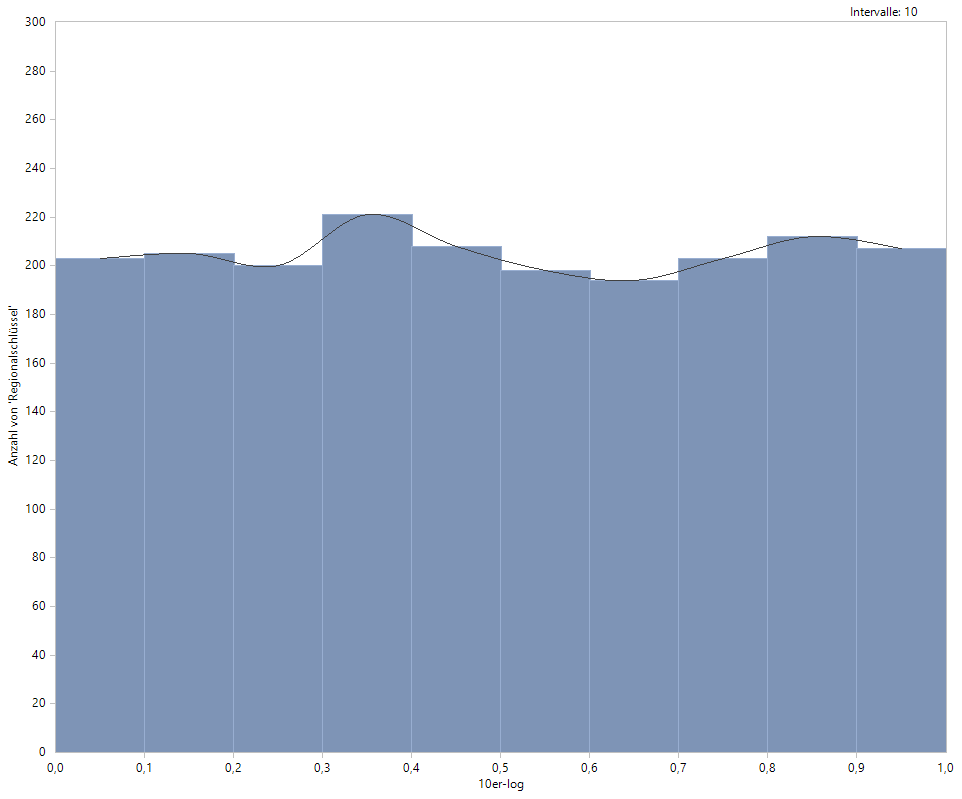
Histogramm der 10er-Logarithmen aus der letzten Spalte

Sind die 10er-Logarithmen gleichverteilt auf [ 0 ; 1), so ergibt sich die folgende Dichtefunktion der normierten Werte aus der 3. Spalte:

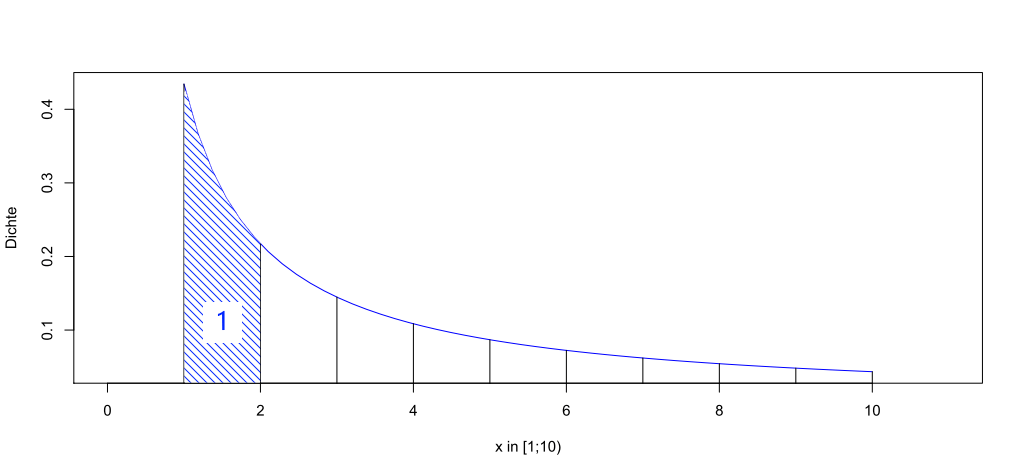
Dichtefunktion der normierten Werte

Wie aus der Grafik noch einmal deutlich wird, kommen Zahlen mit einer kleinen Anfangsziffer häufiger vor. Die Wahrscheinlichkeit einer Ziffer ist durch die zugehörige Fläche unter der Kurve gegeben, welche im Falle der 1 exemplarisch schraffiert worden ist.

Mit Hilfe dieser Dichtefunktion können schon recht viele Verteilungen generiert werden, die alle dem Benfordschen Gesetz folgen. Dies kann etwa in einem zweistufigen Prozess passieren: Zuerst wird eine Zufallszahl gemäß dieser Dichtefunktion generiert und diese wird anschließend mit einer 10er-Potenz multipliziert, deren ganzzahliger Exponent auch einer zufälligen Verteilung unterliegen kann, die zusätzlich auch noch von der ersten Zufallszahl abhängen mag.

Wir benötigen aber normalerweise die umgekehrte Richtung: vom gegebenen Datensatz zu den normierten Daten.

Um die Anwendbarkeit des Benfordschen Gesetzes für einen gegebenen Datensatz rechtfertigen zu können, fehlt es häufig an einer exakten theoretischen Ableitung. Beispielsweise weisen viele bekannte Verteilungen wie Normalverteilungen oder Exponentialverteilungen nicht die notwendige Benfordeigenschaft auf, obwohl zumindest die Ziffernwahrscheinlichkeiten der Exponentialverteilungen schon recht dicht bei den Benfordwerten liegen.

Es würde an dieser Stelle zu weit führen, hinreichende Bedingungen anzuführen, die die Anwendung des Benfordschen Gesetzes zwingend rechtfertigen, aber rechtsschiefe Verteilungen (die Masse der Werte liegt hier eher links), die sich über möglichst viele Zehnerpotenzen erstrecken – wie etwa eine Lognormal-Verteilung mit großer Varianz – passen oft sehr gut.

Die typische Anwendung ist nun also eher im Ansatz zu sehen, den Vergleich mit den erwarteten Häufigkeiten beim Benfordschen Gesetz durchzuführen und bei Abweichungen genauer hinzuschauen.

Die Frage ist nun, welche Manipulationen existieren, die überhaupt erkannt werden können.

Manipulationen, die nicht erfasst werden können, sind zum Beispiel all diejenigen, die die führende Ziffer nicht verändern, wie etwa Multiplikationen mit 10er-Potenzen.

Böse Menschen lesen keine Forschungsblogs, also sei folgender Fehler bei der Verfälschung verraten: Es sind eher händische Manipulationen, die zum Fallstrick werden, wobei die manuell gewählten Werte beispielsweise im für uns günstigen Fall die naive Hypothese gleich häufiger führender Ziffern von oben erfüllen und außerdem so massiv auftreten, dass sie in der Analyse Auswirkungen zeigen.

Eine einzelne Manipulation bleibt also bei dieser Methode unerkannt.

Als mögliche Anwendungsgebiete bieten sich z. B. Wahlergebnisse von vielen Städten oder wie in unserem Falle die Auswertung der auftretenden Zahlen großer Tabellen an.

Erhöhen wir doch einmal sukzessive den Prozentsatz der Schuldenwerte, bei denen die Beträge zufällig durch neue Werte ersetzt wurden, die der naiven Annahme genügen, d. h., bei denen die führende Stelle mit gleicher Wahrscheinlichkeit 1/9 jede Ziffer von 1 bis 9 sein kann.

Manipulierte Daten

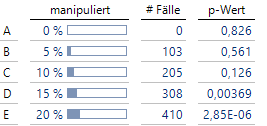
Manipulationen in Höhe von bis zu 10 % bleiben hier noch unentdeckt, aber spätestens wenn 15 % und mehr der originalen Daten durch eigene ersetzt wurden, wird dies durch den Chi-Quadrat-Test erkannt, dessen p-Werte in der letzten Spalte angegeben sind (je kleiner der Wert, desto weniger gehorchen die Daten dem Benfordschen Gesetz!).

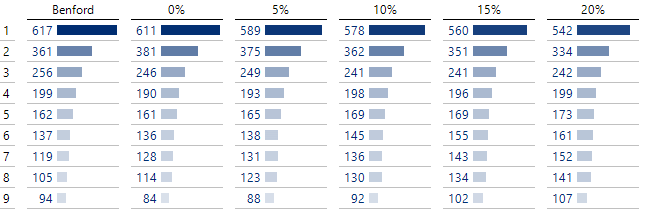
Ziffernhäufigkeiten der manipulierten Daten

Schaut man sich die zugehörigen Häufigkeiten an, so besitzen die manipulierten Verteilungen zwar immer noch die tendenziell schiefe Form der erwarteten Werte, aber die leichte Nivellierung reicht aus, um die Manipulation speziell in den hinteren Spalten mit geringer Irrtumswahrscheinlichkeit aufzudecken.

Übrigens lässt sich auch mit der Verteilung der zweiten Ziffer hinter der führenden Ziffer oder mit der gemeinsamen Verteilung der ersten beiden Ziffern arbeiten. Dann wird es noch schwieriger, Werte zu manipulieren, ohne dass es in der Analyse auffällt.

* Tabellenband zu den Integrierten Schulden der Gemeinden und Gemeindeverbände
Letzter Zugriff am 25.4.2017