Manche Empfehlungssysteme – beispielsweise in der Musik – suchen zu einem vorgegebenen Objekt solche anderen Objekte als Empfehlung aus, die zum aktuell gewählten einen geringen “Abstand” besitzen. Man sollte annehmen, dass eine hohe Anzahl von Features zu einer besonders differenzierten Empfehlung führt. Wie wir heute sehen werden, tauchen jedoch einige störende Haken und Ösen auf!
Bleiben wir beim Beispiel der Musikempfehlung und nehmen an, dass jedes Lied der Welt einen Algorithmus durchläuft und letztendlich ein Vektor von messbaren Eigenschaften erzeugt wird, der stellvertretend für das Musikstück steht. Diese Eigenschaften könnten beispielsweise das Spektrum der verwendeten Frequenzen, den Rhythmus, das Tempo oder die Länge des Stücks beschreiben oder aus diesen Merkmalen – auf welchem Weg auch immer – abgeleitet sein. Alle Eigenschaften seien in der Form numerisch verwertbar, dass sie in einem Vektor zusammengefasst werden können und ein Abstand zwischen zwei Vektoren definiert werden kann.
Unser letztendliches Ziel könnte die automatische Erstellung einer Playlist sein, bei der aufeinanderfolgende Stücke bezüglich der Eigenschaften hohe Ähnlichkeit aufweisen. Gleichzeitig möchten wir auch Monotonie vermeiden. Optimal wäre also in diesem Rahmen eine sich nie wiederholende Folge paarweise ähnlicher Lieder, die sich mäandrierend durch die Musiklandschaft bewegt. Hier konzentrieren wir uns aber erst einmal auf die Generierung der allerersten Empfehlung.
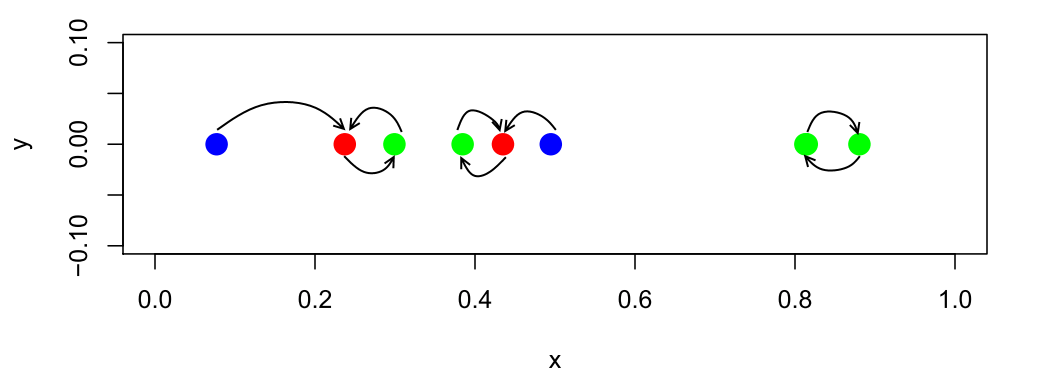
Pfeile zeigen auf den nächsten Nachbarn
Fangen wir mit einem einfachen Beispiel an, bei dem der Vektor nur eindimensional ist (d=1). Seien etwa die bpm (beats per minute) festgehalten und auf das Intervall [0; 1] transformiert worden. Das obige Bild zeigt bei den hier gegebenen acht Stücken durch Pfeile an, welches Lied als Empfehlung folgen würde.
Schon bei diesem einfachen Beispiel fällt auf, dass der Anwender in einer Endlosschleife landen kann, die beiden Stücke rechts würden sich ohne Zusatzmaßnahmen – wie etwa der Streichung bereits gehörter Lieder – immer wieder gegenseitig empfehlen. Erster Nachbar zu sein ist aber keine symmetrische Eigenschaft: Der zweite Punkt von links ist der Nachbar für den ersten, aber für ihn selbst ist der direkte Nachbar durch das dritte Stück gegeben.
Uns interessieren nun genau solche Eigenschaften: Es gibt Lieder (blau), die werden nie von anderen Stücken aus erreicht und deshalb nie empfohlen. Andererseits gibt es Stücke (rot), die von mehreren anderen Songs aus erreicht werden können.
In einer Simulation haben wir nun nicht acht, sondern 1000 x-Werte zufällig erzeugt und gezählt, von wie vielen anderen Liedern Stücke jeweils als direkter Nachbar erreicht werden. Hier ergaben sich die folgenden relativen Anteile:
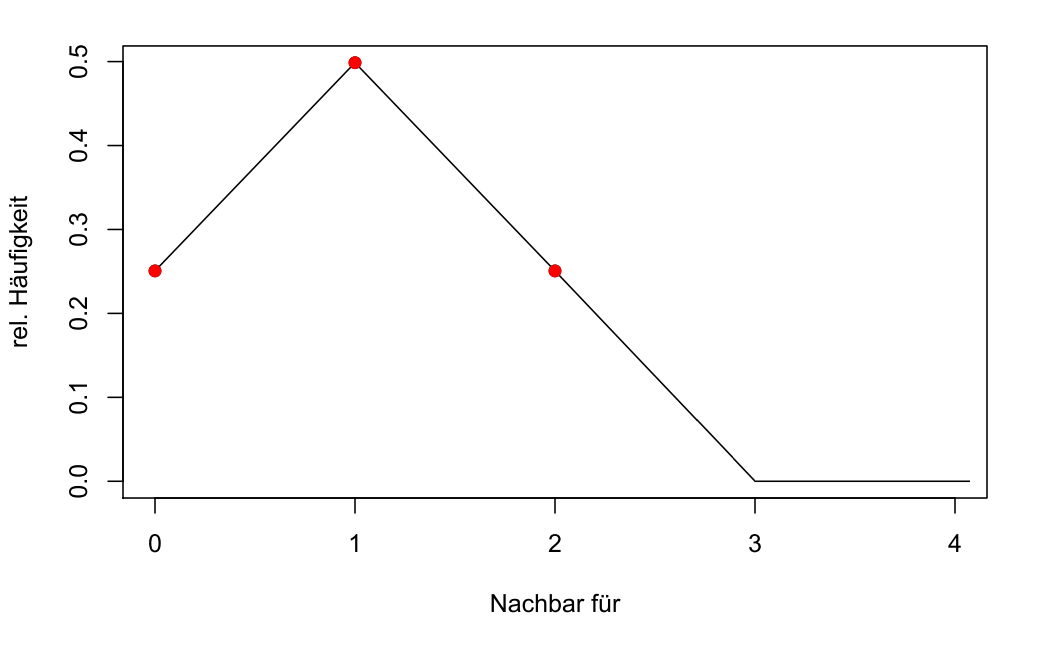
Relative Anteile nach passiver Anzahl von Nachbarn (d=1)
Die Grafik zeigt, dass ca. 1/4 aller Stücke nie empfohlen werden, da sie nicht der direkte Nachbar irgendeines Stückes sind. Etwa die Hälfte der Lieder werden von genau einem anderen Stück aus empfohlen. Ein weiteres Viertel ist die folgende Empfehlung für zwei andere Lieder.
Wie sieht es mit der erwarteten Anzahl aus, d. h. wie viele andere Musikstücke sehen im Schnitt ein zufällig ausgewähltes Stück als ihren direkten Nachbarn? Da jedes Stück genau einen ausgehenden Pfeil aufweist, ist auch die Gesamtsumme der eingehenden Pfeile identisch zur Anzahl der Lieder. Die Erwartung beträgt deshalb genau eins.
Wir erhöhen langsam die Schrittzahl und betrachten nun 2-dimensionale Vektoren. Im folgenden Beispiel haben wir 1000 Punkte auf dem 2-dimensionalen Einheitsquadrat erzeugt:
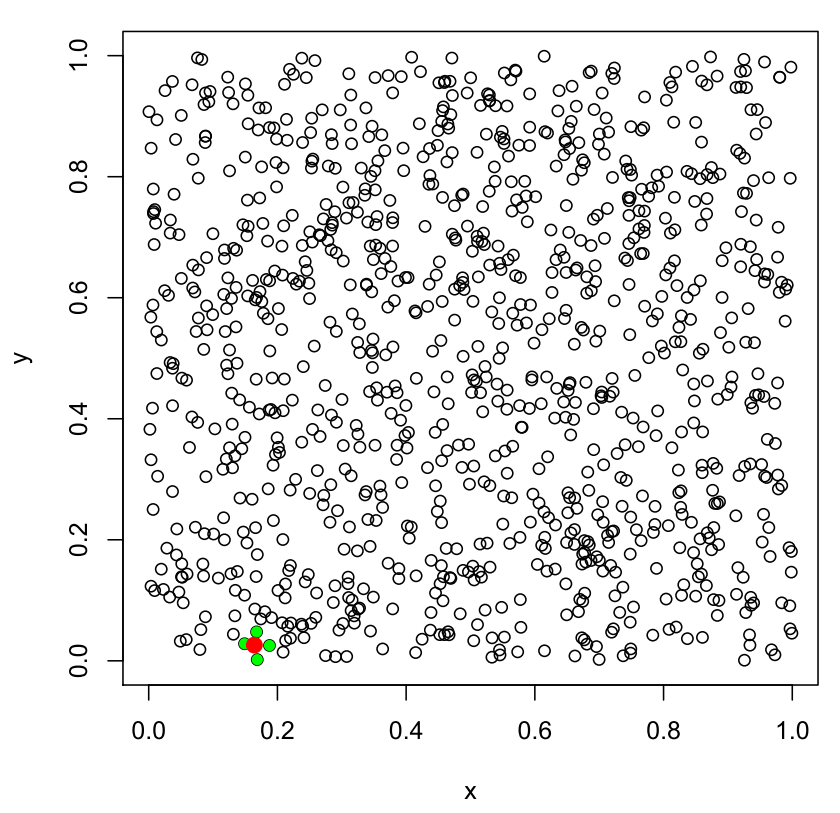
Das einzige Stück, das von 4 anderen Stücken aus empfohlen wird, ist rot markiert!
Von den 1000 Liedern gibt es in diesem Simulationslauf genau eines, das Nachbar von mehr als drei anderen Stücken ist: Das rot markierte wird von 4 anderen Stücken aus empfohlen. Schauen wir auf die Verteilung, so wird deutlich, dass diese Verteilung (d=2) schiefer ist als die für d=1:
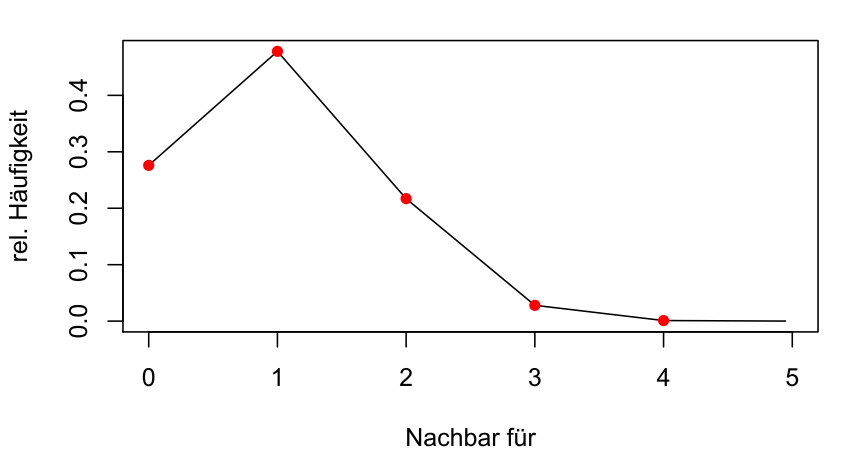
Relative Anteile nach passiver Anzahl von Nachbarn (d=2)
Die erwartete Anzahl von Liedern, die ein bestimmtes zufällig ausgewähltes Stück zum Nachbarn haben, beträgt weiterhin eins. Jedoch hat sich bereits eine leichte Rechtsschiefe eingestellt. Während im Fall d=1 maximal 2 Stücke auf ein Lied weisen, sind es in dieser Simulation bereits 4 Stücke – und dies bei gleicher Liedanzahl (Die Aufgabe, die maximal mögliche Anzahl im 2-dimensionalen Fall zu berechnen, verschieben wir auf später. 5 sind es auf jeden Fall, da die Ecken eines vom Rest isolierten regelmäßigen Fünfecks allesamt den Mittelpunkt als nächsten Nachbarn haben könnten!).
Der Leser ahnt, wohin die Reise geht. Nehmen wir nun an, dass wir sogar 100 Eigenschaften für jedes Lied festgehalten haben. In unserer Simulation haben wir nun 1000 Vektoren aus dem 100-dimensionalen Einheitswürfel erzeugt. Es ist schwierig bis unmöglich, diese Punktwolke angemessen darzustellen, deshalb zeigen wir nur einen Plot der ersten zwei Dimensionen:
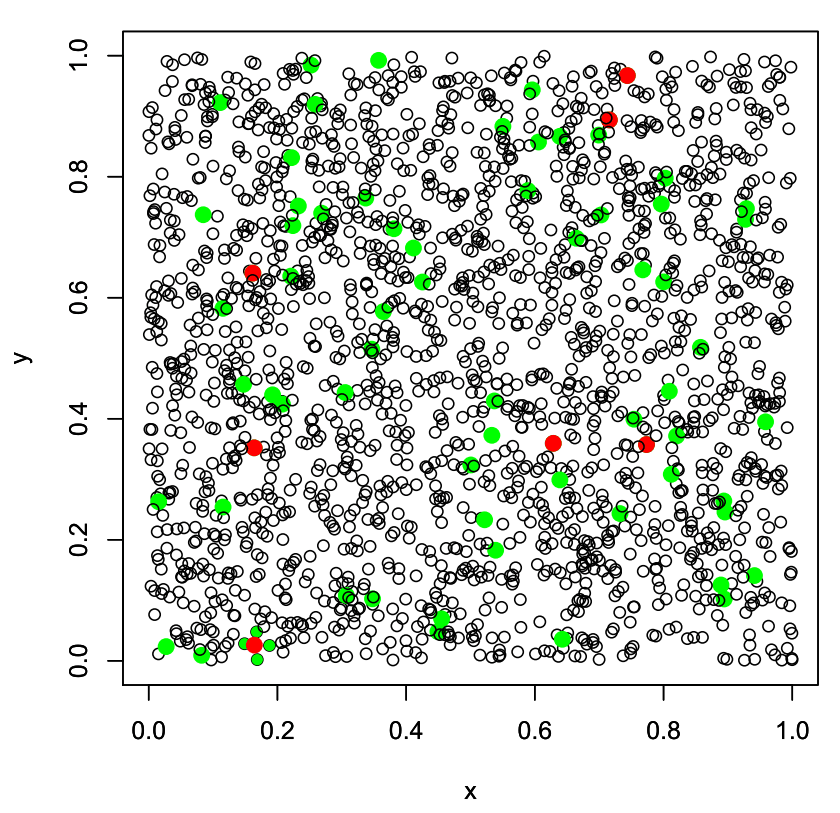
Markiert: Die Musikstücke, die von vielen anderen Stücken empfohlen werden (grün: mehr als 4, rot: mehr als 10)
Hier zeigen die grünen Punkte die Stücke an, die von 4 oder mehr Stücken aus empfohlen werden. Rote Punkte haben sogar 10 oder mehr Fürsprecher. Auch der folgende Plot zeigt, dass die Verteilung immer schiefer wird:
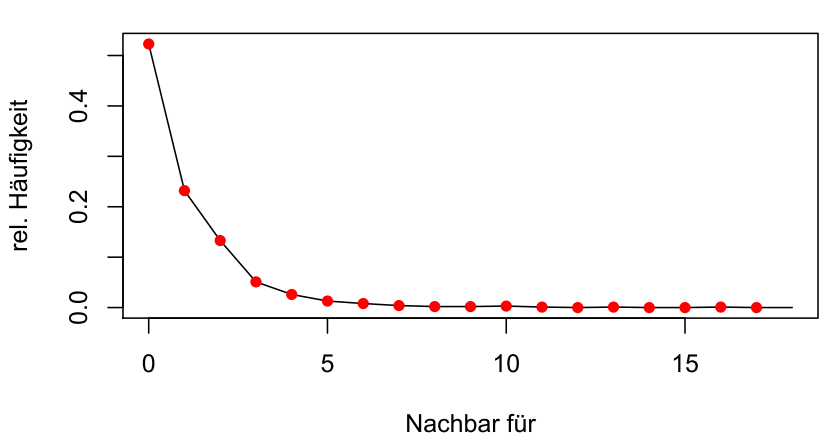
Relative Anteile nach passiver Anzahl von Nachbarn (d=100)
Über die Hälfte der Stücke werden niemals empfohlen, manch andere Stücke haben hingegen 17 “Fans”. Von der Symmetrie im eindimensionalen Fall ist nichts mehr zu sehen. Kein Wunder, dass die aktuelle Forschung versucht, Wege zu finden, die Empfehlungen gleichmäßiger zu streuen.
Nochmals zur Erinnerung: Die Qualität der Musikstücke ist überhaupt nicht in die Vorschlagsgenerierung eingegangen. Diese Ungleichheit entsteht allein durch den Fluch der Hochdimensionalität und einzelne Stücke (“Hubs” genannt) ziehen mit wachsender Anzahl von Features wie ein Schwarzes Loch die Empfehlungen an sich und zeichnen sich somit durch einen hohen Grad an “Hubness” aus. Diese Hubs befinden sich bei der von uns gewählten Gleichverteilung tendenziell näher zur Mitte des 100-dimensionalen Würfels hin, wie die folgende Grafik verdeutlicht.
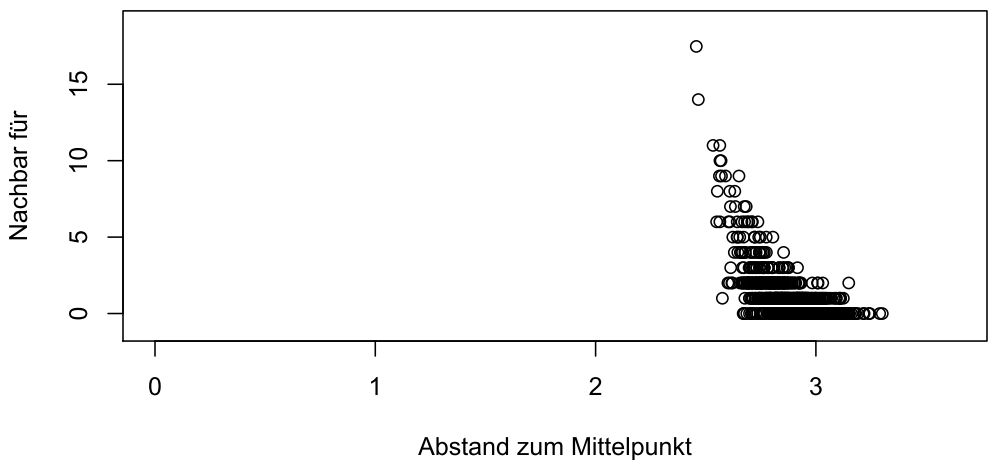
Geringerer Abstand zum Mittelpunkt erhöht tendenziell die Hubness
Die Grafik zeigt übrigens darüberhinaus das paradox anmutende Phänomen, dass mit ansteigender Dimensionalität zufällig im Einheitswürfel gleichverteilte Zufallsvektoren dazu tendieren, gleich weit vom Mittelpunkt des hochdimensionalen Würfels entfernt zu sein.
Wenn man die k nächsten Nachbarn (k>1) als mögliche Folgekandidaten eines Stückes sieht, kann zwar das Problem der Wiederholung eines Stückes gemindert werden. Die erhöhte Hubness einzelner Stücke existiert jedoch weiterhin: Angenommen, das erste Stück der Playlist wird aus allen Stücken per Zufall ermittelt, dann gibt es ab der zweiten Position immer noch die Ungerechtigkeit, dass manche Lieder nie folgen werden, andere aber von vielen Startpunkten aus erreichbar sind.
Die Forschung ist noch im Fluss. Es wurde erkannt, dass sowohl das Abstandsmaß, als auch die Art der gewählten Features Anzahl und Lage der Hubs beeinflussen können. Hubness ist also nicht allein eine Eigenschaft der Daten. Dementsprechend setzen aktuelle Artikel an der Optimierung dieser Größen an, um das Hub-Phänomen so weit wie möglich zu minimieren.
