Aus Indizien auf die tatsächlichen Vorgänge im Hintergrund zu schließen – mit Hidden-Markov-Modellen wird dieser Traum Wirklichkeit. Wir erläutern die Annahmen, die zu erfüllen sind, damit wir aus dem Schatten von Sherlock Holmes treten können.
Die hier beschriebenen Hidden-Markov-Modelle bauen zunächst auf der Annahme auf, dass es eine Menge von Zuständen gibt, zwischen denen nach bestimmten Gesetzmäßigkeiten Sprünge stattfinden. Die zugehörige Theorie wird durch die sogenannten Markov-Ketten beschrieben.
Bei Hidden-Markov-Modellen sind nun im Gegensatz zu normalen Markov-Ketten die Zustände selbst nicht zu beobachten; aus diesem Unterschied folgt nachvollziehbarerweise auch das zusätzliche Attribut „hidden“. Zwar sind nun die Zustände selbst nicht sichtbar, aber es gibt doch Hinweise durch beobachtete Werte, die mehr oder weniger direkt mit dem jeweiligen Zustand der Markov-Kette zu tun haben.
Betrachten wir zunächst das folgende einfache Anwendungsbeispiel einer Markov-Kette mit den drei Zuständen A, B und C:
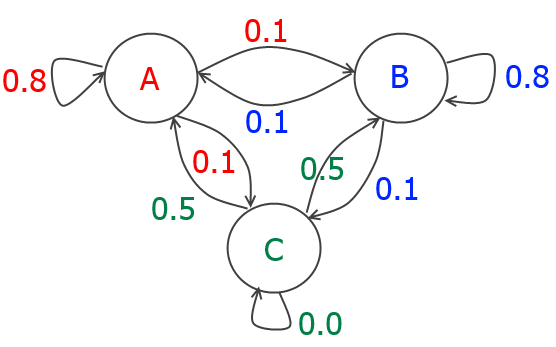
Markov-Kette mit drei Zuständen A, B und C und den Übergangswahrscheinlichkeiten
Man stelle sich eine diskrete Zeitachse t=1, 2, 3, … vor und zu jedem Zeitpunkt springt der Prozess von einem der Zustände zu einem anderen, wobei es erlaubt ist, dass ein Zustand beibehalten wird. Hier handelt es sich um eine homogene Markov-Kette erster Ordnung: Homogen bedeutet, dass die Wahrscheinlichkeit, von einem bestimmten Zustand zu einem anderen zu gelangen, nicht von der Zeit abhängt und die „erste Ordnung“ drückt sich dadurch aus, dass diese Übergangswahrscheinlichkeiten unabhängig von der Vorgeschichte sind. Es ist deshalb unerheblich, wann und wie man zum Zustand A gelangt ist, ob von B, C oder von A selbst. Einmal in A angekommen, wird man mit p=0.8 wieder in A und mit jeweils p=0.1 entweder in B oder C landen. Die Matrix der Übergangswahrscheinlichkeiten lautet hier

Matrix der Übergangswahrscheinlichkeiten
Eine beobachtete Folge zu dieser Markov-Kette könnte für t=1, 2, 3, …, 55 folgendermaßen aussehen:
AAAAAABBBCBBBBBBCBCAAAAAABBBBBAAABBBBAAAAAAACAAAAAAAAAA
Hier wurde angenommen, dass für t=1 jeder der drei Zustände mit einer Wahrscheinlichkeit 1/3 als Startzustand der Kette gewählt werden kann. Im Beispiel hat es A getroffen.
Während der Prozess gerne in A oder B verweilt, wird der Zustand C bei dieser Markov-Kette immer sofort verlassen. Übrigens lässt sich zeigen, dass in einer sehr langen Sequenz der Zustand „C“ mit einem Anteil von etwa 1/11 vertreten ist, aber das ist eher ein Thema für ein späteres Blog.
Kommen wir nun zum schwierigen Teil: Wir nehmen jetzt an, dass diese Folge der Zustände leider nicht direkt beobachtbar ist. Es könnte auch sein, dass die Zustände zwar im Prinzip beobachtbar sind, aber ihre Ermittlung entweder aufwendig oder teuer ist. An die Stelle der originalen Zustände treten nun Indikatoren (im Fachjargon auch Emissionen genannt). Wir wünschen nun durchaus, dass die Indikatoren möglichst trennscharf sind und viel von den eigentlichen Zuständen verraten, aber dieser Wunschzustand wird selten erreicht.
In unserem Beispiel wird nun pro Zeitpunkt eine Zufallsvariable beobachtet, deren Verteilung nur vom Zustand abhängt. Die möglichen Werte seien 1, 2 und 3. Übrigens müssen es nicht zwingend drei Werte sein, es hätten auch zwei oder zehn sein können. Die folgende Tabelle gibt die Wahrscheinlichkeiten wieder, mit denen diese Werte in jedem der Zustände A, B und C beobachtet werden:
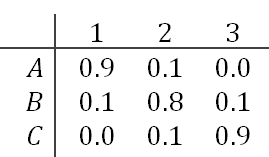
Tabelle der Wahrscheinlichkeiten der beobachteten Werte in Abhängigkeit vom Zustand
Die Tabelle zeigt, dass im Zustand A am häufigsten der Wert 1 erzeugt wird, in B der Wert 2 und in C der Wert 3. Wird eine 3 beobachtet, kann man den Zustand A schon einmal ausschließen; nur B oder C sind mit der Beobachtung 3 vereinbar.
Anstelle der eigentlichen Zustände der ersten Zeile wurden nun beispielsweise die Werte der zweiten Zeile beobachtet:
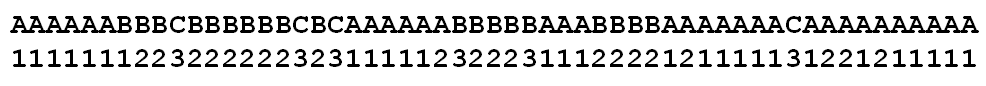
Die unbeobachtete Sequenz der Zustände (oben) und die beobachtete Sequenz der sichtbaren Werte (unten).
Versuchen wir nun die Rekonstruktion der ursprünglichen Folge nur auf der Basis der beobachteten Zahlenfolge. Wir suchen beispielsweise die wahrscheinlichste Folge. Zwei Anforderungen müssen hier simultan erfüllt werden – die Übergänge unserer rekonstruierten Folge müssen zu den Wahrscheinlichkeiten der Übergangsmatrix passen und die beobachteten Werte sollten mit den jeweiligen Verteilungen der angenommenen Zustände gut erklärbar sein.
Bevor wir uns zu sehr in Knobeleien verzetteln, studieren wir die Literatur und erkennen, dass der Viterbi-Algorithmus das Gewünschte tut: Bei bekannter Übergangsmatrix und bei bekannter Verteilung der Zahlenwerte pro Zustand konstruiert er die wahrscheinlichste Folge von Zuständen. Wir haben in folgendem Bild die Tabelle um die rekonstruierte Folge ergänzt und diejenigen Zustände grün markiert, die korrekt erkannt wurden. Fehlerhafte Zuweisungen sind analog rot markiert. In der mittleren Zeile der beobachteten Werte sind diejenigen Werte rot markiert, die untypisch für den Zustand sind, da sie nicht die maximale Wahrscheinlichkeit besitzen, und deshalb „Unruhe“ in den Algorithmus bringen.
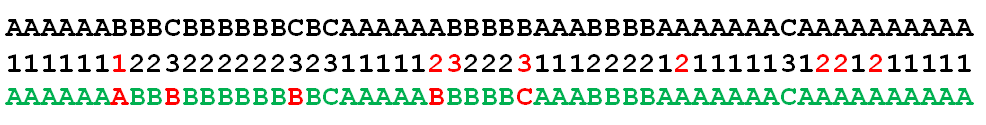
Von oben nach unten: Die Originalfolge der Zustände, die beobachteten Werte (rot: untypischer Wert) und die rekonstruierte Folge (rot: Fehler)
Wie ersichtlich ist, ist die Rekonstruktion schon ganz ordentlich, wenn auch nicht fehlerfrei. Fehler treten hier nur bei Zustandswechseln auf. Der erste Fehler ist verständlich, da beim Wechsel von einer längeren Sequenz mit A beim ersten Auftreten von B weiterhin der eher für A typische Wert 1 zu sehen war.
Die nächsten beiden Fehler erscheinen auch relativ plausibel: Hier lag jeweils eine Teilsequenz BCB mit jeweils typischen Werten 232 vor. Angenommen, nur der mittlere Zustand sei unbekannt und wir nehmen ein Muster BxB mit unbekanntem x an, dann ist die Wahrscheinlichkeit, eine 3 zu beobachten, durch 0.8*0.1*0.8=0.064 gegeben, falls x=B ist (0.8 für den Sprung von B nach B, 0.1 für die Generierung des Wertes 3 und wieder 0.8 für den Sprung von B nach B), während für x=C die Wahrscheinlichkeit nur 0.1*0.9*0.5=0.045 beträgt. Obwohl eine 3 eher typisch für den Zustand C ist, wird unter Berücksichtigung der höheren Übergangswahrscheinlichkeiten der Zustand B vermutet.
Die untypischen Zweien, die im hinteren Teil trotz des Zustands A zu beobachten waren, haben den Algorithmus nicht aus dem Tritt gebracht. Prinzipiell sind bessere Ergebnisse zu erwarten, wenn einige Zustände existieren, die aufgrund der beobachteten Werte zweifelsfrei erkannt werden und als verlässliche Stützstellen in der Zustandsfolge dienen können.
Würde man die Markovkette ignorieren und nur aufgrund der Beobachtungen die Zustände rekonstruieren, mit den Zuordnungen (1->A, 2->B, 3->C), wären 8 anstelle der 5 Fehler aufgetreten.
Wie stark die Verbesserungen sein können, hängt davon ab, wie viel die Beobachtungen selbst über die Zustände aussagen und wie zufällig die Übergänge sind. Im folgenden Beispiel sind die Übergänge deterministisch (A->B, B->C, C->A), nur der Startzustand wird zufällig gewählt. Die beobachteten Werte 1, 2 und 3 sind nicht mehr ganz so typisch für die Zustände A, B und C wie im ersten Beispiel:
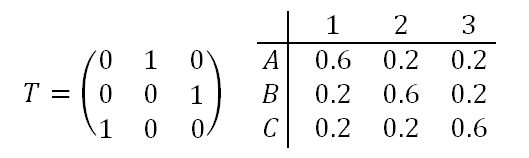
Deterministische Übergänge und schwach markante Emissionen
In diesem Beispiel muss der Viterbi-Algorithmus also nur erkennen, dass die Sequenz, die mit A beginnt, am besten passt und die Sequenz wird dann folgerichtig in ihrer Gänze fehlerfrei rekonstruiert:

Fehlerfrei rekonstruierte Sequenz mit Hidden-Markov-Modell
Bei Rekonstruktion der Folge ohne Verwendung des Hidden-Markov-Modells, wieder mit den naiven Zuordnungen (1->A, 2->B, 3->C), liegt die theoretische Fehlerquote bei 40 Prozent, hier in der konkreten Sequenz treten 27 Fehler auf.
Hidden-Markov-Modelle werden beispielsweise in der Spracherkennung eingesetzt. Im Sprachmodell werden theoretische Gesetzmäßigkeiten für Phonemübergänge hinterlegt und das gesprochene Wort wird zerlegt und aufbereitet und dann als beobachtbare Emissionen der Phoneme interpretiert. Aus diesen wird dann die wahrscheinlichste Phonemfolge geschätzt.
