Millionenbeträge muss man nicht auf Heller und Pfennig ausweisen – es genügt, sie in Millionen anzugeben. Dabei rundet man die Beträge. Das hat mehr Tücken, als man meinen möchte.
Betriebswirtschaftliche Größen zeigen wir gerne in Tabellen. Typisch sind zweidimensionale Kreuztabellen mit Zeilen- und Spaltensummen. In unserem Beispiel haben wir Umsätze nach Produktgruppen und Kunden zusammengefasst:
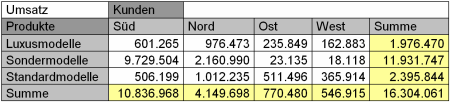
Die Tabelle im Rohzustand
Die Tabelle ist richtig, aber etwas zu genau. Die Lesbarkeit und das Verständnis sind unnötig erschwert. Spätestens im Geschäftsbericht für die Gesellschafter oder in der Bilanz für die Wirtschaftsprüfer wäre das unerwünscht. Im ersten Schritt machen wir die Zahlen kürzer. Wir teilen durch 1000. Im zweiten Schritt runden wir. Hier auf Zwanzigtausender.
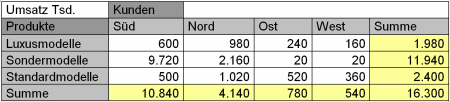
Jeder Wert ist nun auf den nächsten Zwanzigtausender gerundet und in Tausendern angegeben. Peinlich: Manche Summen gehen nicht auf!
Wir kontrollieren die Spaltensummen und erschrecken. Bereits in der ersten Spalte geht die Sache nicht mehr auf. Im Süden machen wir einen Umsatz von 600 + 9.720 + 500 = 10.820. Unsere Skalierung und Rundung weist aber 10.840 aus. Die Summe für Nord ist auch falsch. Die Sondermodelle stimmen ebenfalls nicht. Und richtig falsch ist die Summe über alles. Die Zeilensummen ergeben 1.980 + 11.940 + 2.400 = 16.320. Hingeschrieben haben wir aber 16.300.
Wir erkennen: Wenn wir uns an die üblichen Rundungsregeln halten, dann geht eine Summation nicht zwingend auf. Wenn wir 0,4 + 0,4 addieren, kommt 0,8 heraus. Runden wir aber vorher, dann addieren wir 0 + 0 = 0 und wir sind nicht zufrieden. Soll die Tabelle aufgehen, dann müssen wir die Rundungsregeln verbiegen! Solche schief anmutenden Rundungsregeln gibt es viele. Uns gefällt besonders die Methode des … Kontrollierten Rundens (*).
Glatte Zahlen bleiben damit unverändert. Jede andere wird ab- oder aufgerundet: Aus 23.135 darf 20.000 oder 40.000 werden. Aus der Spaltensumme 770.480 darf also 760.000 oder 780.000 werden.
Natürlich soll die Differenz zu den ursprünglichen Zahlen gering sein. Das ist ein Optimierungsproblem:
- jede Zelle lässt sich auf- oder abrunden
- jede Spalten- und jede Zeilensumme lässt sich auf- oder abrunden
- die Gesamtsumme lässt sich auf- oder abrunden
- alles soll aufgehen:
- Zeilensummen
- Spaltensummen
- Gesamtsumme als Summe der Zeilensummen
- Gesamtsumme als Summe der Spaltensummen
- die Summe der absoluten Differenzen zu den Originalwerten soll minimal sein
Der von uns verwendete Algorithmus löst dieses Problem und wir erhalten diese hübsche Tabelle:
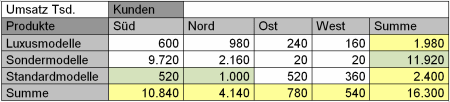
Vom Algorithmus generierte Tabelle, bei der alle Summen aufgehen.
In sich stimmt alles. Grün sind die Zellen, wo wir entgegen der üblichen Konvention gerundet haben:
- 11.931.747 wurde auf 11.920.000 abgerundet
- 506.199 wurde auf 520.000 aufgerundet
- 1.012.235 wurde auf 1.000.000 abgerundet
Der Algorithmus kann auf das gewünschte Rundungsraster eingestellt werden – Tausender, Fünftausender, Zehntausender, Millionen usw. Die Rechenzeit für 50 Zeilen und 10 Spalten beträgt auf einem PC ca. 20 Millisekunden und ist damit schnell genug.
Wie ist das nun? Dürfen wir mal so, mal so runden, damit die Sache aufgeht? Wir haben Steuerberater gefragt. Die sagen: Falsche Summierung kann man nur schwer erklären. Richtige Summierung muss man nicht erklären.
(*): Als guter Einstiegspunkt in die Thematik ist der Artikel „James T. Fagan, Brian V. Greenberg & Bob Hemmig: Controlled Rounding of Three Dimensional Tables, Report Census/SRD/RR-88/02, U.S. Bureau of the Census, Statistical Research Division“ geeignet, der auch den hier behandelten Fall der zweidimensionalen Tabelle ausführlich beschreibt.
