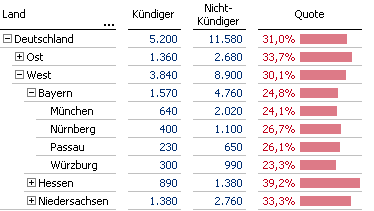
Je mehr Ebenen und je mehr Elemente eine Hierarchie aufweist, umso schwerer fällt es, durch reines Betrachten der komplett aufgeklappten Pivottabelle die vorhandenen Besonderheiten zu entdecken. Da kommt ein Assistent, der die uninteressanten Zweige bei Bedarf schließt, wie gerufen.

Nehmen wir einmal an, dass uns in einem Verlagshaus die Kündigungsquoten einer Zeitschrift interessieren. In Relevanz: Den Zufall zu Fall bringen hatten wir bereits einen Ansatz vorgestellt, unterschiedliche Dimensionen nach ihrem Einfluss auf eine Quote zu sortieren. Die jeweiligen Hierarchien waren jedoch flach und jede Dimension wies nur eine relevante Ebene auf.

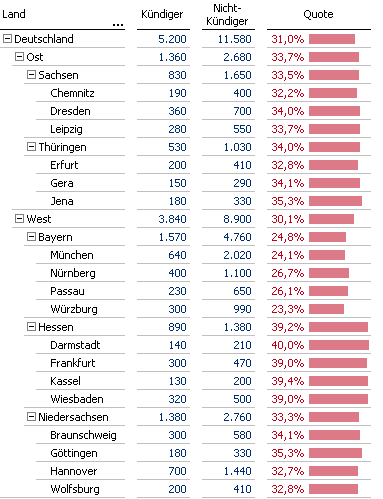
Die aufgeklappte Tabelle der Kündigungsquoten

Hier konzentrieren wir uns hingegen auf eine einzige Dimensionshierarchie, die dafür aber mehrere Ebenen zu bieten hat. In unserem Beispiel ist dies die Hierarchie der Wohnorte der Kunden. Unser Ziel ist es, einen schnellen Überblick über die Struktur der Kündigungsquoten in den Großstädten zu gewinnen.

Der von uns erdachte Algorithmus geht vom momentanen Zustand aus (im Beispiel die komplett dargestellte Hierarchie) und prüft von rechts nach links, ob die Quoten der Nachfolger eines Knotens zueinander ähnlich sind und somit keine relevante Zusatzinformation liefern. Falls diese Annahme zutrifft, wird der Zweig geschlossen. Ein Knoten auf einer um ein Level höher angesiedelten Ebene wird in der nächsten Iteration nur untersucht, wenn sämtliche seiner Kinder eingeklappt wurden.

Unsere Methode fußt auf solider Statistik und wir bewerten mit Methoden der Modellauswahl, ob wir mit dem Zusammenklappen eines Astes auf der sicheren Seite stehen. Je größer die Anzahlen, desto relevanter werden auch kleine Unterschiede. Dazu bedarf es prinzipiell keiner weiteren Parameter. Nach der ersten internen Iteration sähe die Tabelle folgendermaßen aus:

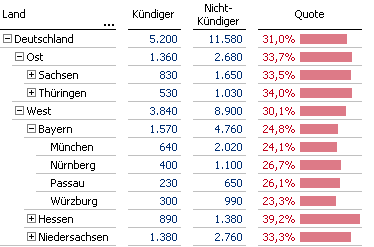
Tabelle nach der ersten für den Anwender nicht sichtbaren Iteration

Abgesehen von Bayern wurden alle Zweige der Bundesländer zusammengeklappt. In Bayern selbst waren die Unterschiede der Quoten der Städte unter Berücksichtigung der Anzahlen zu groß.

In einer weiteren internen Iteration wird der Bereich Ost zugeklappt und die vereinfachte Tabelle, die dem Anwender letztendlich präsentiert wird, sieht folgendermaßen aus:

Die automatisiert vereinfachte Tabelle, die dem Anwender präsentiert wird.

Wir benutzen bewusst einen Bottom-Up-Ansatz, da es ja sein könnte, dass sich die Quoten in Ost und West sehr ähneln, obwohl die Quoten in den Bundesländern voneinander stark abweichen und ein Top-Down-Ansatz dann bereits bei Deutschland keinen Anlass sähe, nach Ost und West aufzuklappen.

Nehmen wir als zweites Beispiel den Anteil der Frauen an der Leserschaft, dann sähe die maximale Tabelle folgendermaßen aus:

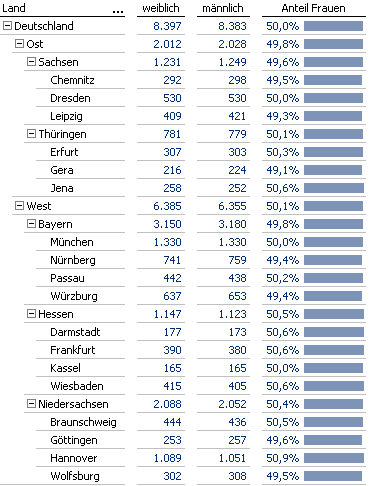
Der Anteil der Frauen an der Leserschaft.

Der Algorithmus fasst diese Quoten zur Quintessenz “Hier gibt es nichts zu sehen!” zusammen:

Fazit: Der Anteil der Frauen hängt nicht von der geographischen Lage ab.

Der Algorithmus stellt sicher, dass in einem zugeklappten Zweig keine Überraschungen lauern können, aber es wäre denkbar, dass der Anwender laxere Vorstellungen des Begriffs Ähnlichkeit besitzt und auch noch größere Abweichungen ignorieren möchte. Durch die Einführung eines Parameters ließe sich auch diese Anforderung einbauen, sodass auch noch bei eigentlich leichteren Abweichungen ein Zweig zusammengeklappt wird und tendenziell kleinere Tabellen generiert werden.

Natürlich kann der Algorithmus auch so eingesetzt werden, dass er von einer beliebigen Ausgangskonstellation gestartet wird, sodass beispielsweise nach dem manuellen Schließen eines Zweiges der Algorithmus erneut ausgeführt werden kann und unter Umständen die Pivottabelle weiter vereinfacht.

Denkbar wäre es auch, den Grad der akzeptierten Unterschiedlichkeit der Quoten anhand der manuell geschlossenen Zweige zu lernen und bereits bei der Fortsetzung des Algorithmus anzuwenden.