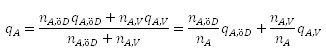Additiv und positiv – diese beiden Attribute lassen auf gutmütige Kennzahlen schließen. In einer Hierarchie stellt der Wert eines Elements dann sogleich die Obergrenze der möglichen Werte der Nachfolger auf tieferen Ebenen dar. Wenn es in ganz Bayern 200 Kunden gibt, kann in Nürnberg keine höhere Anzahl vorliegen. Bei den teuflischen Quoten hingegen sorgt der Blick nach unten zuweilen für einigen Schwindel.
Der Vertriebsleiter der Chair AG möchte die Aktivitäten seiner Untergebenen während einer Werbeaktion beurteilen und den abschlussstärksten Verkäufer des neuen Stuhlmodells „Precisio Relax“ mit einer Sonderprämie beglücken. Während der Aktion wurde dieses Modell jedem Kunden nur in einer Menge von genau 50 Stühlen zu einem vergünstigten Preis angeboten.

Die Erfolgsquoten der drei Vertriebler
Die Tabelle zeigt ihm, dass die drei Vertriebler A, B und C gleichermaßen fleißig waren, jeweils 40-mal das Stuhlpaket vorgestellt haben, und dass sich A mit der höchsten Anzahl von Abschlüssen die Prämie redlich verdient hat. Gemäß dem Motto „Von den Besten lernen“ möchte der Vertriebsleiter den Kollegen B und C anhand der Daten illustrieren, auf welche Ursachen sich der Erfolg von A zurückführen lässt.
Dieses Stuhlpaket wurde an Versicherungen und den öffentlichen Dienst verkauft, und logischerweise gehört es zur Analyse, die Quoten der drei Vertriebler in diesen zwei Kundengruppen anzuschauen:

Die Erfolgsquoten der drei Vertriebler nach Branche
Der Vertriebsleiter nimmt zur Kenntnis, dass die Erfolgsquoten im öffentlichen Dienst tendenziell höher liegen, doch dann stutzt er: In jedem der zwei Segmente, und mehr gibt es auch nicht, liegt A nach den Erfolgsquoten auf dem letzten Platz und der in der allgemeinen Übersicht letztplatzierte C führt auf einmal die Quoten-Rangliste in beiden Segmenten an. Wie kann das sein, dass der in allen Segmenten abschlussstärkste Verkäufer in der Gesamtanalyse auf den letzten Platz rutscht? Welchem Ergebnis sollte der Vertriebsleiter trauen und vor allem, wer sollte die Sonderprämie erhalten?
Das Phänomen, dass sich die Ordnung von Quoten durchgehend auf disjunkten Teilmengen umkehrt, ist als Simpson-Paradoxon bekannt. Häufig wird es in der Form zitiert, dass ein Medikament A eine höhere Heilungsquote hat als B, obwohl sowohl bei Frauen, als auch bei Männern die Heilungsquote von A niedriger ist als diejenige von B.
Ein anderes gern vorgebrachtes Beispiel zeigt die geringere Aufnahmequote an Universitäten von Frauen im Vergleich zu Männern und die Detailanalyse ergibt dann, dass es in jedem Fachbereich tendenziell eher umgekehrt ist.
Wie kommt dieses Paradoxon zustande? Wir nehmen einmal die Kollegen A und C ins Visier: Angenommen, die Erfolgsquoten in den Segmenten seien fest vorgegeben mit den Werten wie oben:
Die Anzahlen der kontaktierten Kunden in den Segmenten seien mit
bezeichnet. Die gesamte Erfolgsquote von A berechnet sich zu
Hier liegt der Schlüssel zum Verständnis: Die gesamte Erfolgsquote ist ein mit den Anteilen gewichtetes Mittel der Segmentserfolgsquoten. A kann sich somit zwischen 0.6 (wenn er sich nur dem öffentlichen Dienst widmet) und 0.2 (wenn er sich nur den Versicherungen widmet) bewegen. Ebenso bewegt sich C zwischen 0.8 und 0.3, je nach Schwerpunkt seiner Aktivitäten.
Wenn also C in beiden Segmenten eine höhere Erfolgsquote als A besitzt, kann hier das Simpson-Paradoxon nur deshalb auftreten, weil erstens die Erfolgsquote von A im leichteren Segment des öffentlichen Dienstes mit 0.6 höher liegt als die Erfolgsquote 0.3 von C im schwereren Segment der Versicherungen, und zweitens, weil der Anteil der Aktivitäten von A im leichteren Segment genügend hoch war und der Anteil von C genügend niedrig.
Die folgende Grafik illustriert die Situation sehr schön, dass trotz der Ordnungen C>B>A, die in beiden Segmenten gelten, für die Gesamterfolgsquote A>B>C zu beobachten ist:
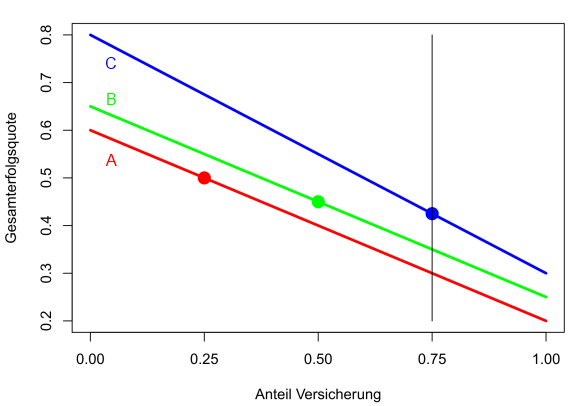
Die Berechnung der Gesamterfolgsquote nach Anteil der Aktivitäten im Segment der Versicherungen
Das Simpson-Paradoxon mit Bezug auf A und C kann somit bspw. nie auftreten, wenn die Erfolgsquote von A im öffentlichen Dienst unterhalb der Erfolgsquote von C bei den Versicherungen liegt. Wie die Grafik ebenfalls leicht vermittelt, tritt auch kein Paradoxon auf, wenn die investierten Anteile der Aktivitäten von A und C für jedes Segment identisch sind. Hätte A auch einen Anteil von 75% bei den Versicherungen, so wäre seine erwartete Gesamtquote mit 0.25*0.6+0.75*0.2=0.3 ebenfalls niedriger als die 0.425 von C.
Zur Illustration sei die folgende Tabelle gegeben, die eine Prognose der Ergebnisse unter der Annahme zeigt, dass jedem Vertriebler jeweils 20 Kunden aus jedem Segment zugewiesen worden und somit identische Gesamtzahlen in den Segmenten wie in der Ausgangssituation zu beobachten wären. Die Erfolgsquoten der Vertriebler auf der Ebene der Branchensegmente sind als unverändert angenommen.

Hochrechnung der Erfolgsquoten bei ausgeglichener Zuordnung zu Branchen
In diesem Fall mit gleichen Anteilen kann das Simpson-Paradoxon nicht auftreten, und die Gesamtreihenfolge ist identisch zu den Segmentreihenfolgen C>B>A.
Für die Beurteilung der Verkaufsleistung ist nun von Bedeutung, wie die Zuordnung der Vertriebler zu den Kundensegmenten entstanden ist.
Entspringt die Zuordnung bspw. der Anordnung des Vertriebsleiters oder ist sie aufgrund der regionalen Verantwortlichkeiten entstanden, so sollte C dafür kompensiert werden, dass er es mit dem schwierigeren Kundenkreis zu tun hatte. Da er in beiden Segmenten die jeweils höchste Erfolgsquote vorzuweisen hat, verdient er die Sonderprämie. Richtig wäre es also hier, mit den bedingten Erfolgsquoten pro Segment zu arbeiten.
Sollten jedoch A, B und C aus einem größeren Pool ohne weitere Vorgaben des Vertriebsleiters die Kunden ausgewählt haben, ist unsere Überschrift „Nur bedingt richtig“ nur bedingt richtig. In diesem Falle sollte A für seine Cleverness belohnt werden, da er erkannt hat, dass die Betreuung von Kunden des öffentlichen Dienstes die besseren Erfolgschancen verspricht.
Natürlich muss angenommen werden, dass es keine weiteren Dimensionen gibt, die das Ergebnis beeinflussen können.