Um das Wissen einer großen Anzahl von Prüfungskandidaten einschätzen zu können, werden häufig Multiple-Choice-Tests eingesetzt. Durch Raten können Zufallstreffer entstehen, die nicht auf tatsächlicher Kenntnis beruhen. Wie gelangt man zu einer gerechten Bewertung? Sollte man raten oder nicht?
Bei einer massiven Basis von Prüflingen führt die Verwendung von Aufgaben, die eine Antwort in Form eines Freitexts verlangen, zu einem erheblichen Aufwand bei der Korrektur. Weiterhin könnten Schwierigkeiten auftreten, die Fairness bei der Bewertung durchgehend auf einem konstant hohen Niveau zu halten.
In solchen Situationen haben sich Multiple-Choice-Tests etabliert. Üblicherweise gibt es in der Standardform pro Frage k (bspw. k = 4) mögliche Antworten, von denen exakt eine einzige richtig ist.
Einen Haken gibt es jedoch: Werden Punkte auf richtige Antworten vergeben, so können auch durch simples Raten Punkte erzielt werden:
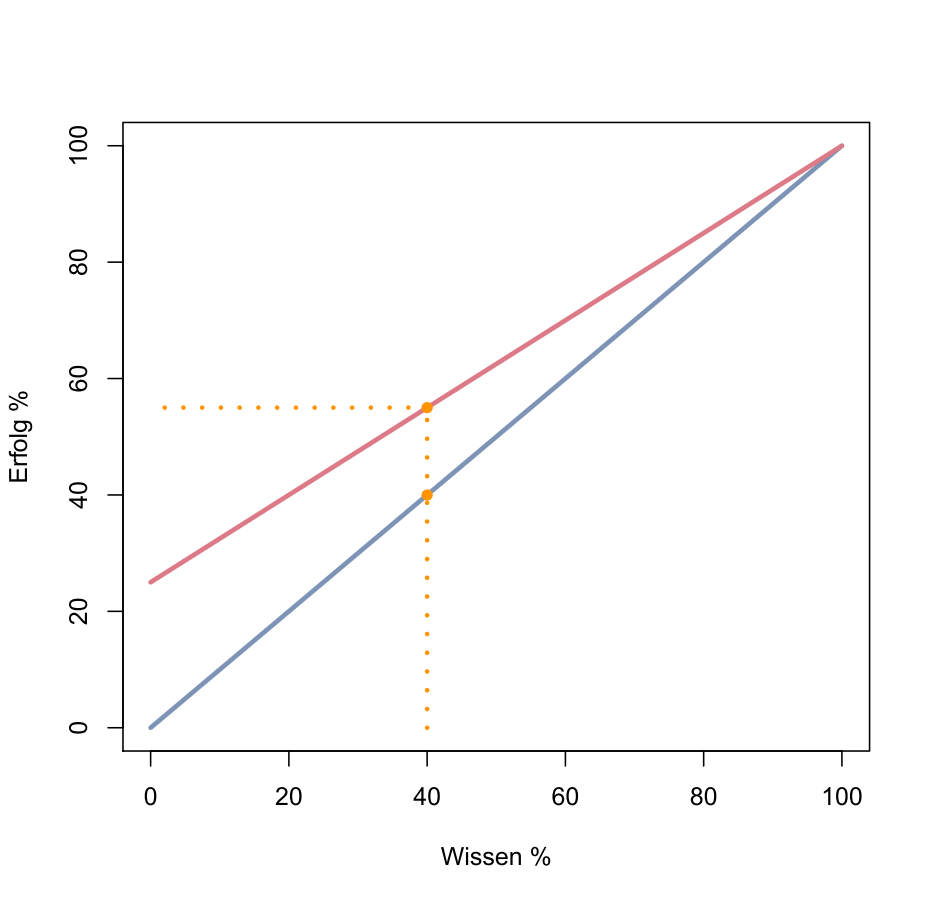
Mehr Schein als Sein durch Raten
Eine Prüfung soll den Stand des tatsächlichen Wissens wiedergeben: Die blaue Linie repräsentiert dieses Ziel; jemand, der bspw. 40 % der Materie beherrscht, sollte auch etwa 40 % der repräsentativen Testaufgaben lösen. Durch Raten bei den Aufgaben, bei denen das Wissen fehlt, wird aber in diesem Fall (k = 4) im Schnitt ein Gesamterfolg von E = 40 % + 0.25 *60 % = 55 % erzielt, also ein deutlich höherer Wissensstand vorgegaukelt, als tatsächlich vorhanden ist.
Jemand, der eine Frage auslässt, erhält hierfür sicher 0 Punkte. Damit jemand, der nur rät, zumindest im Mittel gleichgestellt wird, müssen falsche Antworten bestraft werden. Hier nehmen wir an, dass beim Raten aus allen k Antworten jede einzelne Antwort mit gleicher Wahrscheinlichkeit 1 / k gewählt wird. Mit P = 1 / k ist die Antwort richtig und es wird ein Punkt erzielt. Mit P = (k-1) / k ist die Antwort falsch und es werden S Punkte abgezogen.
Die erwartete Punktzahl soll 0 sein, d. h., es muss gelten:
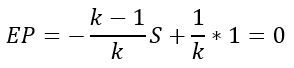
Die erwartete Punktzahl soll bei Raten 0 betragen!
Lösen dieser Gleichung führt zu einer Strafe von S = 1 / (k-1), also beispielsweise zu einem Abzug von 1 / 3 Punkt im Fall von k = 4 möglichen Antworten.
D. h., im Mittel ist es egal, ob wir bei einer Fragestellung, bei der wir absolut keine Ahnung haben, die Frage nun einfach nicht beantworten (sichere 0 Punkte) oder ob wir raten (1 Punkt bei richtiger Antwort, 1 / 3 Punkt Abzug bei falscher Antwort, aber im Mittel 0 Punkte).
Trotzdem unterscheiden sich die zwei Strategien. Nehmen wir einmal vereinfachend an, dass jede Person eine Frage entweder sicher richtig beantwortet oder überhaupt keine Ahnung hat, welche Antwort in Frage kommen kann, also unter anderem keine Antwort ausschließen kann.
Weiterhin sei jede Person in ihrer Selbsteinschätzung ohne Fehler, d. h., sie weiß ganz genau, welche Fragen sie richtig beantworten kann und welche nicht.
Dies bedeutet bei rationalem Vorgehen, dass die zum Wissen gehörenden Fragen richtig beantwortet werden und es nur darum geht, bei Wissenslücken zu raten oder die Frage unbeantwortet zu lassen.
Im folgenden Szenario liegen 100 Multiple-Choice-Aufgaben vor. Eine teilnehmende Person habe ein Wissen von x, d. h., x Fragen werden sicher richtig beantwortet.
Die erste Strategie, bei Wissenslücken auf eine Antwort zu verzichten, birgt keine Überraschungen. Eine Person mit Wissen x wird unter den genannten Annahmen auch x Punkte erzielen. Es ergibt sich ein einfacher streng linearer Zusammenhang – die Identität! – zwischen Wissen und Punktzahl, der in der linken Seite der folgenden Grafik dargestellt ist (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!):
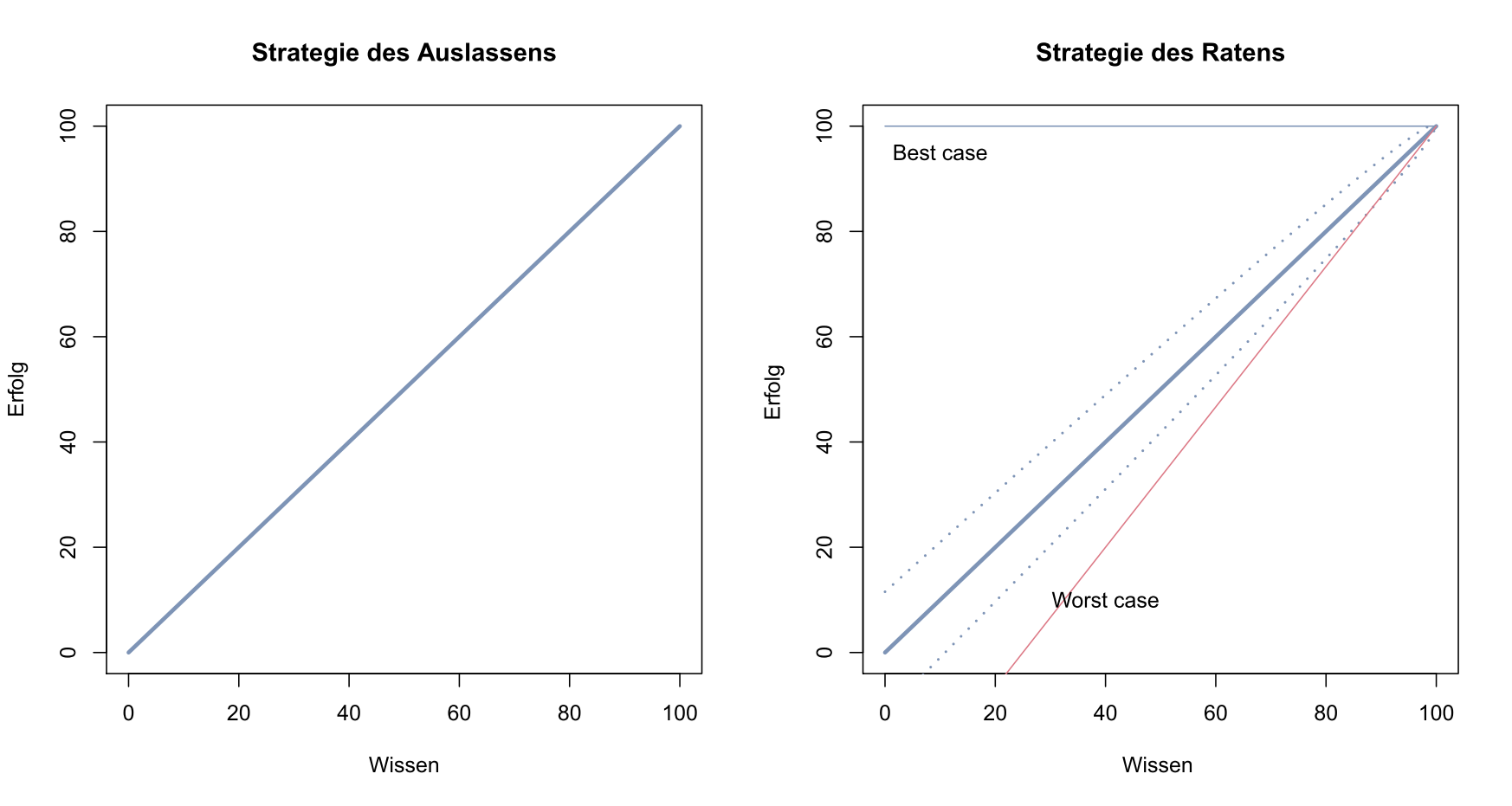
Bei Wissenslücke Frage auslassen oder raten?
Wenn jemand mit Wissen x die zugehörigen Fragen richtig beantwortet, und bei den übrigen 100 – x Fragen rät, passiert folgendes (siehe Diagramm rechts):
Im besten Falle rät er alle 100 – x Fragen richtig und erzielt somit 100 Punkte, obwohl dieser Fall mit sinkendem Wissen immer unwahrscheinlicher wird. Im schlechtesten Fall versemmelt er die restlichen 100 – x Fragen und bekommt insgesamt x – (100 – x) / 3 = 4 x / 3 – 100 / 3 Punkte. Jemand mit Wissen 40 erhält somit im Worst Case 160 / 3 – 100 / 3 = 20 Punkte. Bei geringem Wissen unterhalb von x = 25 ist es sogar möglich, in den negativen Bereich zu gelangen.
Die gestrichelten Kurven addieren/subtrahieren zu/von der erwarteten Diagonale die zweifache Standardabweichung. Im Bereich zwischen den Kurven sollte der Großteil der tatsächlich erzielten Punktzahlen landen.
Eine risikofreudige Person sucht eher nach der maximal möglichen Belohnung und wählt somit das Raten. Eine risikoscheue Person mit Wissen x hingegen möchte eher die Mindestpunktzahl absichern und verzichtet auf das Raten, da hier die mögliche Punktzahl auch geringer als das vorhandene Wissen x ausfallen könnte.
Besonders interessant ist es, wenn zwei Gruppen mit identisch verteiltem Wissen, aber gegensätzlichem Risikoverhalten aufeinandertreffen.
Seien hier zwei Gruppen jeweils der Größe 200 gegeben, deren Wissensverteilung näherungsweise einer Glockenkurve ähnelt, wobei eine relative homogene Gruppe mit vergleichsweise geringer Streuung des Wissens um 50 herum angenommen wird. Vereinfachend nehmen wir an, dass jedes Mitglied einer Gruppe einen zugeordneten Wissenszwilling in der anderen Gruppe mit exakt gleichem Wissen besitzt:
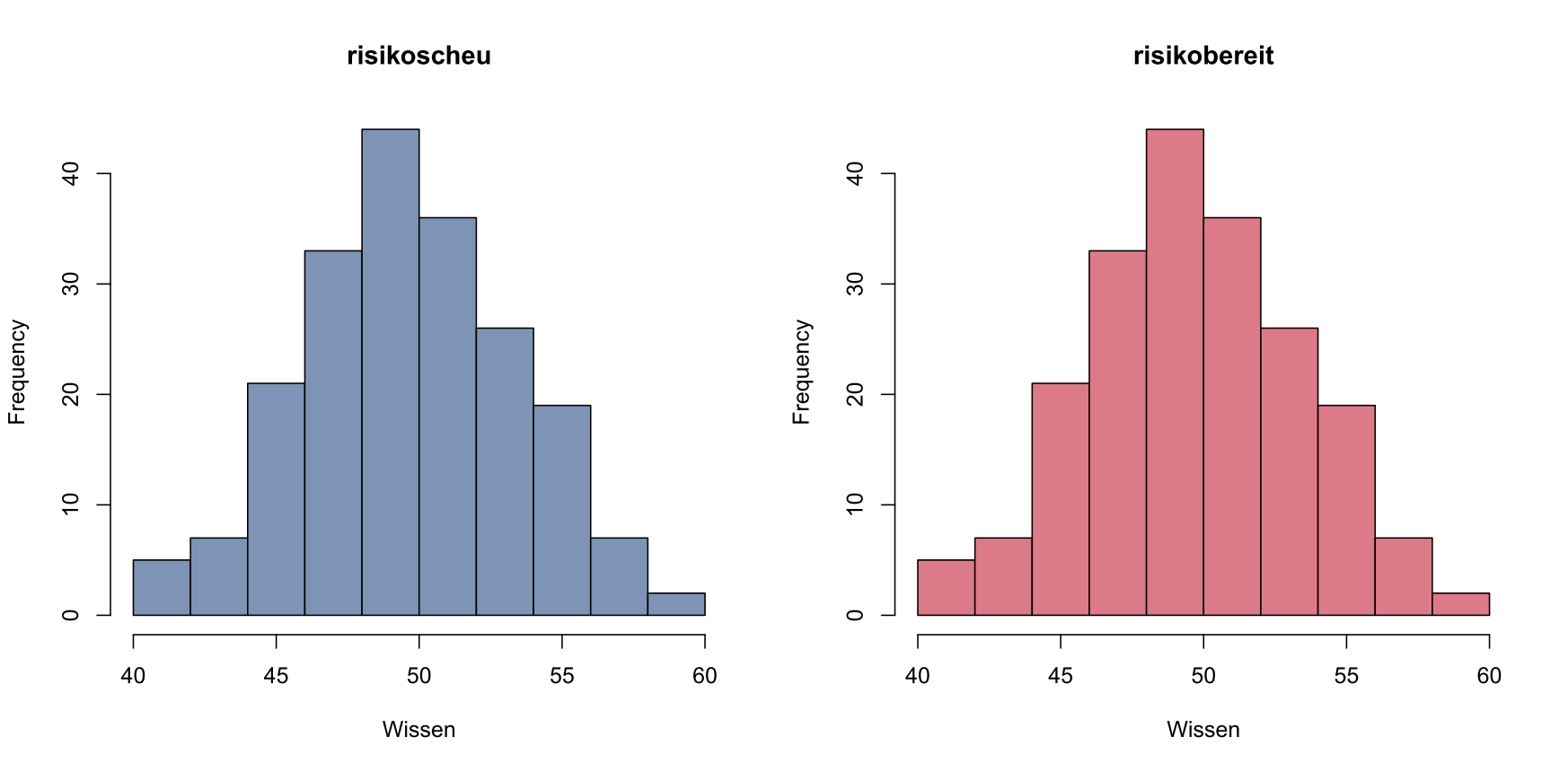
Zwei Gruppen mit identischer Wissensverteilung
Nun wird der Test durchgeführt und die Auswertung der Testergebnisse auf den beiden Gruppen ergibt die folgenden Diagramme:
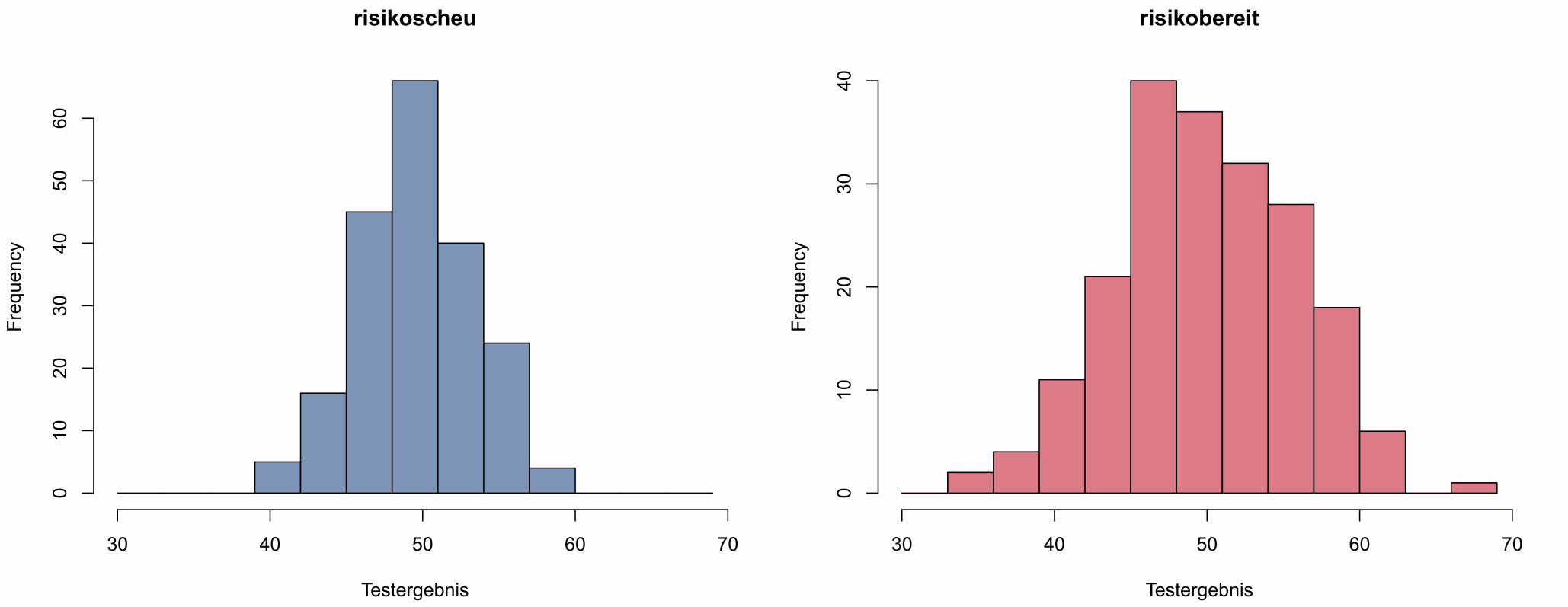
Testergebnisse der beiden Gruppen
Die Werte der risikoscheuen Gruppe links haben sich nicht verändert; das Histogramm sieht nur aufgrund der geänderten Achseneinteilung etwas anders aus. Die Werte der risikobereiten Gruppe hingegen streuen viel mehr.
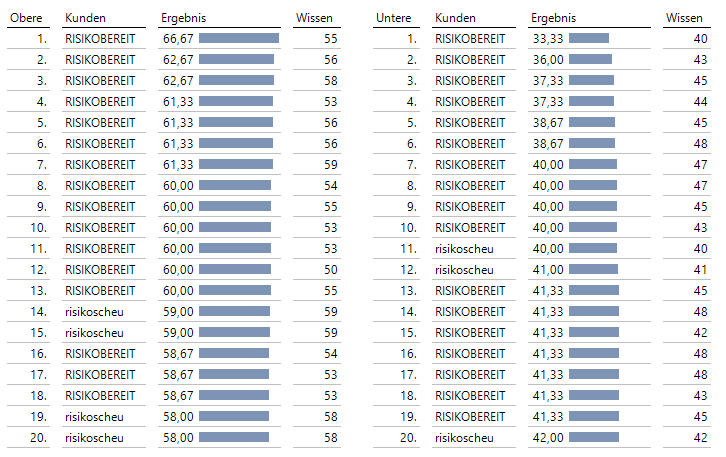
Nehmen wir beispielsweise an, dass die Top 20 des Tests ein Stipendium erhalten werden. Werfen wir somit einen Blick auf die Enden der Rangfolge:
Die ersten 13 Plätze werden sämtlich von Mitgliedern der risikobereiten Gruppe belegt. Weiterhin ist ersichtlich, dass sich die risikobereiten Teilnehmer der oberen Gruppe allesamt durch das Raten verbessert haben. Von den 20 besten Ergebnissen gehören nur 4 Prüflinge der risikoscheuen Gruppe an.
Ähnlich sieht es am unteren Ende aus; auch hier stammen nur 3 von 20 aus der risikoscheuen Gruppe. Nahe der roten Laterne haben sich die risikoaffinen Teilnehmer jedoch verschlechtert!
Überspitzt ausgedrückt: Risikoscheu sichert den Platz im Mittelfeld.
Bisher hatten wir die erwartete Punktzahl betrachtet; diese beträgt bei zufälligem Raten, als auch bei Weglassen der Antwort exakt null. Nun nehmen wir nicht die Erwartung, sondern schauen auf die Wahrscheinlichkeit, sich bei Raten nicht zu verschlechtern. Werden diese Wahrscheinlichkeiten für alle möglichen Werte des Wissens von 0 bis 99 berechnet – jemand mit Wissen 100 muss nicht mehr raten -, ergibt sich überraschenderweise eine Sägezahnkurve:
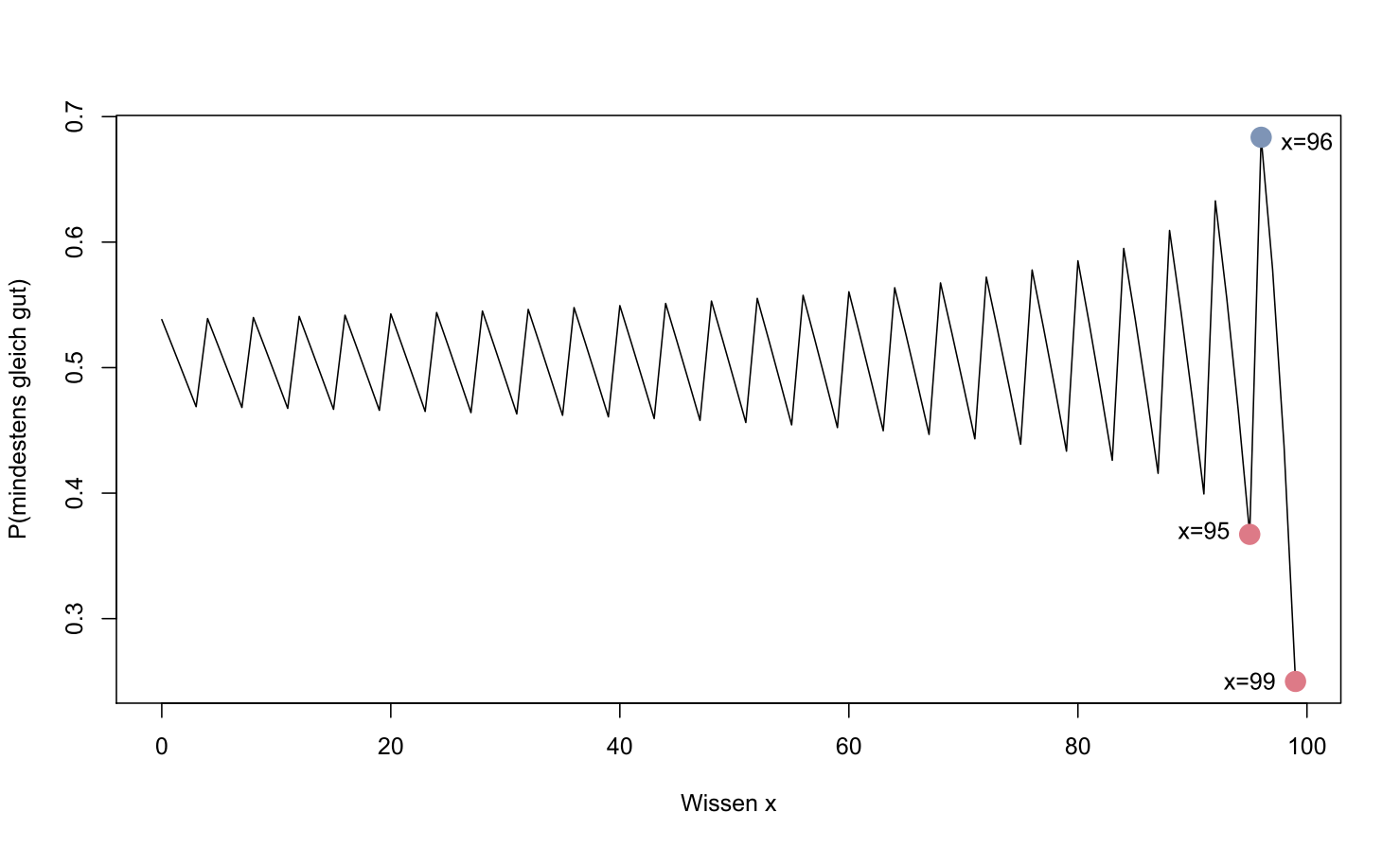
Wahrscheinlichkeit, sich bei Wissen x mit Raten nicht zu verschlechtern
Wenn eine Erwartung 0 ist, folgt daraus nicht zwingend, dass die Wahrscheinlichkeiten für Werte > 0 und für Werte < 0 gleich groß sein müssen. Setzen Sie 1 Euro beim Würfeln und erhalten 6 Euro, wenn die 6 kommt, ist der erwartete Gewinn EG = -1 + 1 / 6 * 6 = 0, aber mit 5 / 6 verlieren Sie und mit 1 / 6 gewinnen Sie.
Wie kommen also die Werte aus der Grafik zustande?
Jemand mit Wissen x = 99 landet mit p = 0.25 bei 100 Punkten, wenn er die richtige Antwort rät, und mit p = 0.75 bei 98.67 Punkten, wenn er auf die falsche Antwort gesetzt hat. Er wird sich also mit einer deutlich höheren Wahrscheinlichkeit verschlechtern, auch wenn der mögliche Zugewinn mit + 1 höher ausfällt als das mögliche Absacken um – 1 / 3.
Eine Person mit x = 96 verschlechtert sich nur, wenn alle 4 restlichen Fragen falsch beantwortet werden, die Punktzahl beträgt dann 96 – 4 * 1 / 3 ~ 94.67. Mit einer einzigen richtigen Antwort ergibt sich mit 96 + 1 – 3 * 1 / 3 = 96 bereits eine unveränderte Punktzahl. Dass 4 Antworten falsch geraten werden, passiert mit p = 0.75 * 0.75 * 0.75 * 0.75 ~ 0.316. Es folgt, dass mit p = 1 – 0.316 = 0.684 keine Verschlechterung eintritt.
Schließlich verschlechtert sich eine Person mit x = 95, wenn sie nur eine Antwort richtig rät, da die zusätzlichen Punkte 1 – 4 * 1 / 3 = – 1 / 3 betragen. Erst mit zwei richtigen Antworten gerät sie wegen 2 – 3 * 1 / 3 = 1 in die Gewinnzone. Zwei oder mehr richtige Antworten treten aber nur etwa mit einer Wahrscheinlichkeit 0.367 auf.
Es lässt sich ausrechnen, dass sich Personen mit einem Wissen x, das durch 4 teilbar ist – dann ist auch die Anzahl der restlichen Fragen 100 – x durch 4 teilbar -, im Vorteil befinden, da es bei ihnen ausreicht, ein Viertel der Antworten, also 25 % richtig zu raten. Diese durch vier teilbaren Anzahlen x = 4 * v bilden die lokalen Maxima in obigem Diagramm.
Besonders schwer haben es hier in unserem Fall mit 100 Fragen die Personen mit einem Wissen x, das bei Division durch vier einen Rest 3 ergibt, also, wenn x = 4 * v – 1 ist. Sie müssen im Vergleich zu den Leuten mit x = 4 * v eine Antwort mehr richtig raten, haben aber gleichzeitig auch nur eine einzige Aufgabe mehr zur Verfügung. Die Person mit x = 95, also mit 5 offenen Fragen musste bereits 2 / 5 Antworten richtig haben, also 40 %.
Besonders extrem geraten Ergebnisse bei völliger Homogenität des Wissenstandes. Hätten alle 400 Teilnehmer einen Wissensstand von 50, blieben die risikoscheuen Teilnehmer bei der 50 stehen. Jemand der rät, landet mit 13 richtig geratenen Antworten bei 50 + 13 – 37 / 3 = 50.67 Punkten, mit 12 richtigen Antworten bei 50 + 12 – 38 / 3 = 49.33 Punkten.
Dies heißt, dass sich jemand, der über der erwarteten Anzahl von 50 * 1 / 4 = 12.5 richtigen Antworten liegt, gegenüber der risikoscheuen Gruppe verbessert, und dass jemand, der darunter liegt, gegenüber der anderen Gruppe schlechter abschneidet. Ein Verharren auf der Punktzahl ist hier bei Raten nicht möglich.
Die Wahrscheinlichkeit für ein besseres Abschneiden lässt sich über eine Binomialverteilung berechnen; sie beträgt gerundet 0.489. Schlechter als die Vergleichsgruppe wird man mit p = 0.511.
Für den einzelnen Rater sind die Chancen der Verbesserung bzw. Verschlechterung hier also nahezu ausgeglichen, wenn überhaupt, dann gibt es leichte Nachteile für den Rater.
Rechnen wir nun noch aus, wie groß die Wahrscheinlichkeit ist, dass sich aus der Gruppe von 200 Ratern mindestens 20 verbessern, so ergibt abermals eine Binomialverteilung das Ergebnis, dass dieser Wert nahezu 1 ist. Dies wird auch plausibel, wenn bedacht wird, dass sich in der Erwartung etwa 200 * 0.489 ~ 98 Prüflinge verbessern werden (und etwa 102 verschlechtern) und es selbst bei Schwankungen so gut wie sicher mehr als 20 Personen werden, die sich verbessern.
Für die 20 Stipendien heißt das, dass diese so gut wie sicher nur an die risikobereite Gruppe vergeben werden!
Es gibt Studien, die belegen, dass zumindest ein merklicher Anteil der Männer risikobereiter ist. Für den konkreten Teilnehmer ist das Raten relativ fair und er wird sich im letzten Beispiel – mit einer minimal größeren Wahrscheinlichkeit – eher verschlechtern als verbessern. Risikobereite Menschen werden aber vermehrt in den Top-Ergebnissen zu finden sein (und in den Flop-Ergebnissen, aber die interessieren nicht so sehr).
Mehr Mut zum Risiko in einer Gruppe führt somit oft zur besseren Sichtbarkeit von Mitgliedern an der Spitze. Für den konkret benannten Teilnehmer lässt sich der Platz an der Sonne hingegen nicht erzwingen.
Das genannte Vorgehen ist natürlich nur eine mögliche Strategie. Um Raten gänzlich zu unterdrücken, könnte etwa eine viel höhere, abschreckend wirkende Strafpunktzahl angesetzt werden. Die Möglichkeit, dem Probanden die Darstellung von Teilwissen zu ermöglichen, indem beispielweise mehrere Antworten angekreuzt werden dürfen, obwohl weiterhin nur eine einzige richtig ist, führt zu weiteren Ansätzen, deren Untersuchung lohnenswert ist.