Möglichst exakte Nachfrageprognosen helfen, Out-of-Stock-Situationen und exzessive Abschriften zu vermeiden. Im vorliegenden Beitrag schauen wir auf einige Aspekte, die es dabei zu beachten gilt.
Stellen wir uns einen Supermarkt vor und betrachten einen leicht verderblichen Artikel, der dem Kunden maximal einen Tag offeriert werden darf und bei Nichtkauf am Abend der Vernichtung zugeführt wird. Die leitende Person der Filiale hat bisher eher einfach kalkuliert und jeden Tag eine Menge von exakt 8 Einheiten in die Auslage legen lassen.
Nach hundert Tagen soll nun überprüft werden, ob nicht eine bessere Strategie existieren könnte. Dazu wurde ermittelt, wie viele Einheiten jeweils pro Tag verkauft wurden und daraus wurden Anzahlen von Tagen mit einem vorgegebenen Absatz errechnet:
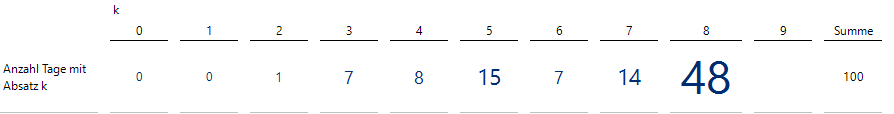
Anzahl der Tage mit einem Absatz k (k = 0, …, 8)
Hier haben wir für Absatzmengen von 0 bis 8 die Anzahl der Tage dargestellt, an denen der jeweils vorgegebene Absatz auftrat. Ein Absatz von 9 oder mehr kann prinzipiell nicht vorkommen, wenn nur 8 Einheiten angeboten werden. Wir haben deshalb dieses Feld leer gelassen und keine 0 verwendet.
Genau genommen interessiert uns aber nicht der Absatz, sondern eher die an einem Tag vorhandene Nachfrage!
Solange der Absatz 7 oder weniger beträgt, entspricht der Absatz der Nachfrage, die somit vollständig befriedigt wird. Hier gibt es keinen Unterschied zwischen den beiden Größen.
Bei einem Absatz von 8 hingegen ist nicht klar, ob die tatsächliche Nachfrage exakt 8, vielleicht 10 oder sogar 15 betragen hat. Es liegen somit bei der Nachfrage sogenannte zensierte Daten vor, da durch den „Versuchsaufbau“ mit einem fixen Angebot 8 vielleicht vorhandene Nachfragen von mehr als 8 prinzipiell nicht beobachtet werden können.
Ein Absatz von 8 ist somit gleichbedeutend mit einer Nachfrage „8 oder mehr“.
Nehmen wir in einem Gedankenexperiment einmal an, dass nicht 8, sondern vielleicht 50 Einheiten angeboten wurden, sodass die tatsächliche Nachfrage nicht durch ein möglicherweise zu knapp bemessenes Angebot beschnitten wurde und der Absatz immer exakt gleich der Nachfrage ist.
Das folgende Zahlogramm zeigt drei mögliche beobachtete Verteilungen der unzensierten Daten, die allesamt bei Zensur (Angebot = 8) zu der tatsächlich beobachteten Konstellation mit 48 Tagen mit 8 verkauften Einheiten geführt hätten:

Hypothetische Anzahlen von Tagen mit einer Nachfrage größer als 7
Wie findet man nun die am besten geeignete Anpassung, wenn durch Angebotsbeschränkung auf 8 all diese Werte in ihrer Detailliertheit gar nicht beobachtet werden konnten? Wenn das Angebot dauerhaft auf 8 beschränkt ist, wird man nie den quantitativen Verlauf der Verteilung für Werte des Angebots von 8 und mehr besser einschätzen können.
Eine Möglichkeit einer plausiblen Extrapolation liefert die Verwendung einer parametrischen Verteilung wie etwa der Poissonverteilung, deren prinzipielle Eignung durch theoretische Überlegungen begründet werden kann:
Üblicherweise besuchen an einem Tag viele Kunden einen Supermarkt, von denen jedoch jeder einzelne für das gegebene konkrete Produkt nur eine geringe Kaufwahrscheinlichkeit aufweist. Die Summe der Käufer ist dann binomialverteilt mit Parametern n (= Anzahl der Kunden) und p (= Kaufwahrscheinlichkeit). Das obere Diagramm der folgenden Abbildung zeigt die Wahrscheinlichkeiten für eine Binomialverteilung mit n = 1000 und p = 0.7 %.
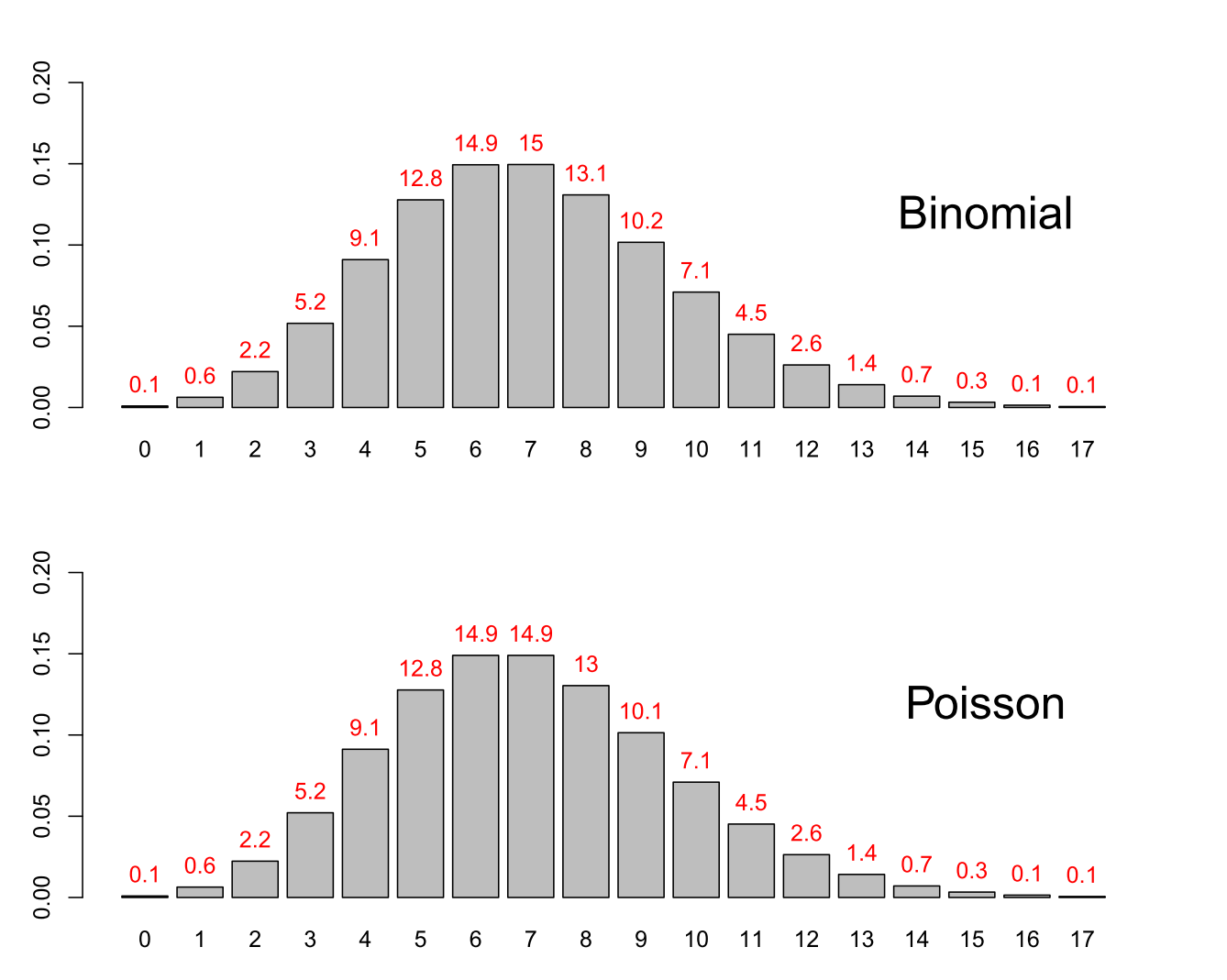
Minimale Unterschiede zwischen Binomialverteilung (oben) und Poissonverteilung (unten)
Wenn p sehr klein ist (hier ist p mit 0.007 genügend klein) und n sehr groß, lässt sich zeigen, dass die Binomialverteilung durch eine Poissonverteilung angenähert werden kann. Diese ist in der unteren Hälfte der obigen Abbildung sichtbar. Wie die über den Säulen sichtbaren Prozentzahlen zeigen, ist der Unterschied zwischen beiden Verteilungen minimal.
Die Poissonverteilung besitzt nur einen Parameter Lambda, der einfach auf das Produkt n * p = 1000 * 0.007 = 7 gesetzt wird.
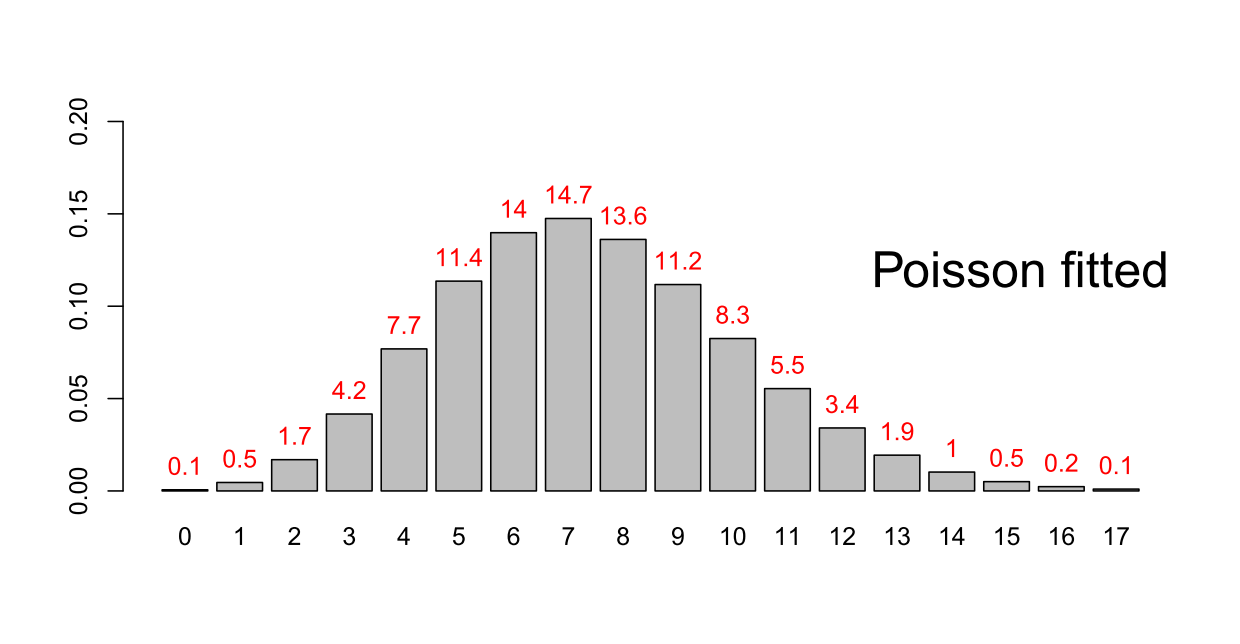
Es lässt sich nun die Wahrscheinlichkeitsfunktion des Absatzes berechnen, falls das Angebot auf 8 fixiert wird. Dazu werden alle Wahrscheinlichkeiten der Poissonverteilung für k = 8, 9, 10, … addiert und für den Absatz ausschließlich der 8 zugeordnet. Die folgende Abbildung zeigt diesen Vorgang (beachten Sie bitte die unterschiedlichen Skalen der beiden Abbildungen!):
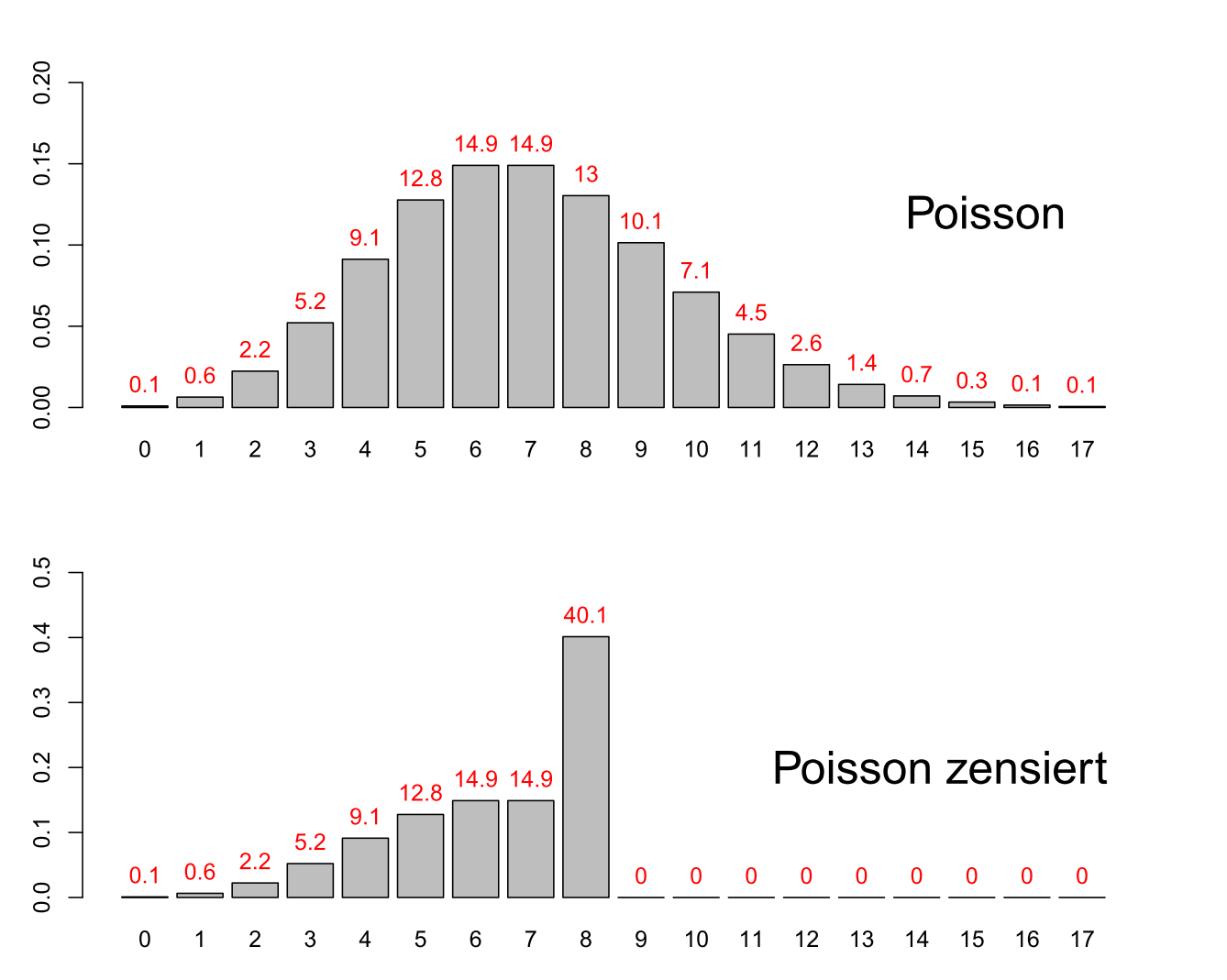
Aus der unzensierten Verteilung (oben) berechnete Wahrscheinlichkeitsfunktion des Absatzes (unten)
Wir versuchen nun, den Wert des Parameters Lambda zu optimieren, mit dem Ziel, die Wahrscheinlichkeit, die tatsächlich aufgetretenen 100 Absatzwerte zu beobachten, zu maximieren.
Bei einer unzensierten Stichprobe schätzt man den Parameter Lambda einfach durch den mittleren Absatz. Hier ist das nicht zielführend, da der Schätzer für Lambda, der sich aus der ersten Tabelle durch die Berechnung (2*1 + 3*7 + 4*8 + 5*15 + 6*7 + 7*14 + 8*48) / 100 zu 6.54 ergibt, durch die Zensur zu niedrig ausfällt, da ja die wahre Nachfrage systematisch unterschätzt wird.
Eine etwas komplexere Berechnung des Maximum-Likelihood-Schätzers, die berücksichtigt, dass ein Absatz von 8 stellvertretend für alle möglichen Werte der Poissonverteilung von 8 und mehr steht, führt zu einem Schätzer für Lambda ~ 7.385. Es lässt sich nun die komplette Wahrscheinlichkeitsfunktion der Poissonverteilung rekonstruieren und so tun, als ob es die Zensur nie gegeben hätte. Das Ergebnis sieht optisch ähnlich aus zu der Abbildung von eben mit Lambda = 7, im Vergleich zu dieser sind die Gewichte nur leicht nach rechts verschoben:
Wie kann nun diese Poissonverteilung genutzt werden?
Zunächst stellt man fest, dass die Schwankungsbreite der möglichen Nachfragen groß ist. Wir sagen auch nicht eine konkrete Nachfrage vorher („Heute wollen 11 Personen einen Kürbis kaufen“), sondern unsere Vorhersage ist eben die gesamte Verteilung.
Wie diese Verteilung genutzt wird, hängt nun von der Zielsetzung ab.
Kommt von der Marktleitung die Vorgabe, dass ein nachgefragtes Produkt mit maximal 10 Prozent Wahrscheinlichkeit ausverkauft sein darf, ergibt eine Berechnung durch Addition der Wahrscheinlichkeiten, dass der gesuchte Wert bei einem Angebot von 11 Einheiten liegt: Die Wahrscheinlichkeit einer Nachfrage von 12 oder mehr beträgt hier 7.3 Prozent. Bieten wir nur 10 Einheiten an, tritt eine Nachfrage größer als 10 bereits mit 12.8 Prozent auf.
Vielleicht wird aber auch mehr Wert auf geringe Abschriften gelegt. Ist die Vorgabe, durchschnittlich höchstens etwa 2 zu vernichtende Einheiten zuzulassen, so könnten wir 9 Einheiten anbieten. Eine Einheit vernichten wir, falls die tatsächliche Nachfrage 8 beträgt, zwei Einheiten bei einer Nachfrage von 7 usw.
Die erwartete Anzahl von zu vernichtenden Einheiten beträgt dann ca. 1*0.136 + 2*0.147 +3*0.14 + 4*0.114 + 5*0.077 + 6* 0.042 +7* 0.017+ 8 *0.005 + 9*0.001 ~ 2.1.
Schließlich können beide Kriterien simultan berücksichtigt werden. Dazu wird einer verkauften Einheit ein positiver Deckungsbeitrag zugeordnet, ein zu vernichtendes Produkt wird mit einem negativen Beitrag bestraft. Es lässt sich dann für jedes Angebot der erwartete Nettoertrag berechnen und dann das Angebot mit maximalem Wert wählen. Sei bspw. der Stückdeckungsbeitrag eines verkauften Produktes 1 und die Strafe – vielleicht in Gestalt des Einkaufspreises – für ein zu vernichtendes Produkt 2, dann ergibt sich ein optimales Angebot von 6. Die folgende Grafik veranschaulicht die Ermittlung dieser optimalen Angebotsmenge:
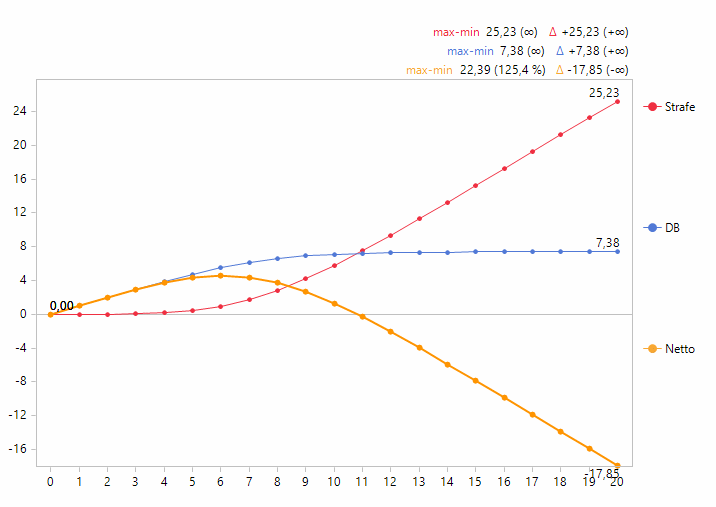
Erwartete Werte von DB, Strafe und Nettobeitrag für verschiedene Bestände
Wenn wir das Angebot von 0 aus erhöhen, wird zunächst jede Einheit so gut wie sicher verkauft und der erwartete DB steigt nahezu linear. Irgendwann führt ein erhöhtes Angebot nicht mehr zu einem erhöhten Absatz und der DB stagniert.
Für die Strafe sieht es umgekehrt aus: Da zunächst so gut wie jedes Produkt verkauft wird, bleibt die erwartete Strafe bei 0. Irgendwann muss jede zusätzliche Einheit vernichtet werden und trägt zu einer dann linear wachsenden erwarteten Strafe bei.
Der Nettobeitrag ergibt sich als Differenz der beiden Beiträge und nimmt ein Maximum an, das hier bei 6 liegt.
Das gezeigte Vorgehen ist nur ein Baustein auf dem Weg zu einer vollständigen Predictive-Analytics-Anwendung. Bisher wurde vereinfachend angenommen, dass von Tag zu Tag keine Änderungen der Nachfragewahrscheinlichkeiten auftreten.
Gibt es Einflüsse auf den Parameter Lambda, beispielsweise allgemeine Einflüsse wie Wetter oder Jahreszeit oder produktspezifische Einflüsse wie etwa eine Preisaktion, so kann versucht werden, eine Modellierung in Abhängigkeit von diesen Werten anzusetzen.
Da ja möglicherweise viele Produkte simultan betrachtet werden, könnte es auch zielführend sein, die für alle Produkte gültige Anzahl der Supermarktbesucher n in Abhängigkeit der allgemeinen Einflüsse wie Jahreszeit, Ferien, Wochentag oder Wetter zunächst getrennt zu modellieren.
Da n dann selbst als Zufallsvariable zu sehen ist, kann die Verteilung der tatsächlichen Nachfrage auch als gewichtete Mischung aus vielen Poissonverteilungen mit unterschiedlichen Parametern Lambda = n * p gesehen werden. Wenn das Lambda nicht allzusehr schwankt, sollte eine einzelne „mittlere“ Poissonverteilung als Näherung für die Disposition ausreichen.
Kurzfristige zeitliche Einflüsse sind auch denkbar. Beispielsweise könnte die Spargelnachfrage zu Beginn der Saison deutlich höher liegen als nach ein paar Wochen der Gewöhnung. Aufeinanderfolgende Nachfragen könnten auch korreliert sein, auch negativ, wenn bspw. erhöhte Käufe an einem Tag zu tendenziell geringerer Nachfrage am Folgetag führen.
Schließlich werden auch Korrelationen zwischen den Nachfragen verwandter Produkte existieren. Man sieht, dass die Komplexität eines Modells beliebig große Ausmaße annehmen kann.
Prinzipiell sollte aber klar geworden sein, dass eine alleinige Konzentration auf die Verkaufszahlen die Nachfrage unterschätzen wird, falls Out-of-Stock-Situationen nicht dokumentiert oder bei der Modellierung nicht berücksichtigt werden.