Die schönsten Visualisierungen leiden, wenn einzelne extrem große Werte vorliegen. Beispielsweise bei der Portfolioanalyse drängen sich die übrigen Objekte in der Ecke und ein schneller Überblick auch über die weniger auffälligen Fälle aus der zweiten Reihe wird verhindert. Wir beschreiben ein paar Ideen, den Einfluss der Ausreißer auf die Darstellung zu begrenzen!
Stellt man in einer Portfolioanalyse zwei Kennzahlen gegenüber, hier beispielsweise Umsatz und Materialkosten der Kunden, dann wirkt das erzeugte Diagramm wenig differenziert, wenn ein oder zwei sehr dominante Kunden vorliegen.
Hier hat der umsatzstärkste Kunde fast den sechsfachen Umsatz des Zweitplatzierten und bereits den 36-fachen Umsatz des Drittplatzierten erzielt und ist sehr weit von der Masse der anderen Kunden entfernt. Ähnliche Disproportionen liegen auch bei den Materialkosten vor.
Der Begriff „Ausreißer“ sollte an dieser Stelle eher vom statistischen Standpunkt interpretiert werden: Der umsatzstärkste Kunde ist natürlich gern gesehen und nicht etwa unerwünscht. Es wäre schön, wenn alle Kunden so wären wie dieser.
Wir schauen hier somit eher auf den störenden Einfluss dieses positiv besetzten Ausreißers bei einer graphischen Überblicksdarstellung, wie sie etwa durch die Portfolioanalyse gegeben ist.
Auch wenn hier die Abhängigkeit von einem einzelnen Kunden extrem groß ist, möchte man doch auch die Lage der entwicklungsfähigen Kunden aus der zweiten Reihe besser einschätzen können.
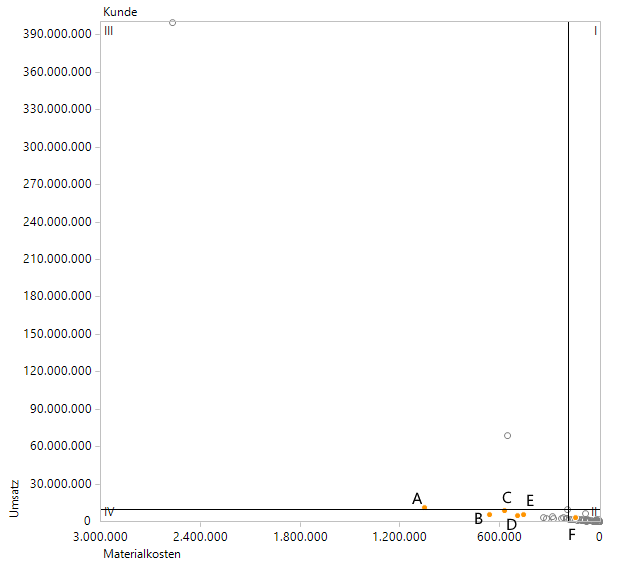
Ein dominanter Kunde drängt den Rest in die Ecke
Hier haben wir im Grafikprogramm eine willkürlich ausgewählte Menge von 6 Kunden aus der zweiten Reihe mit A bis F (der Kunde F befindet sich irgendwo in der Punktwolke rechts unten) gelabelt, die wir in den alternativen Darstellungen wiederfinden werden.
Eine Möglichkeit, eine eingängige Ansicht zu erzeugen, besteht in der Anwendung eines interaktiven Filters: Die darzustellenden Objekte (also ohne die zwei Ausreißer) werden mit der Maus per Rahmen eingegrenzt und somit markiert, und anschließend wird die Option „Nur markierte anzeigen“ aktiviert:
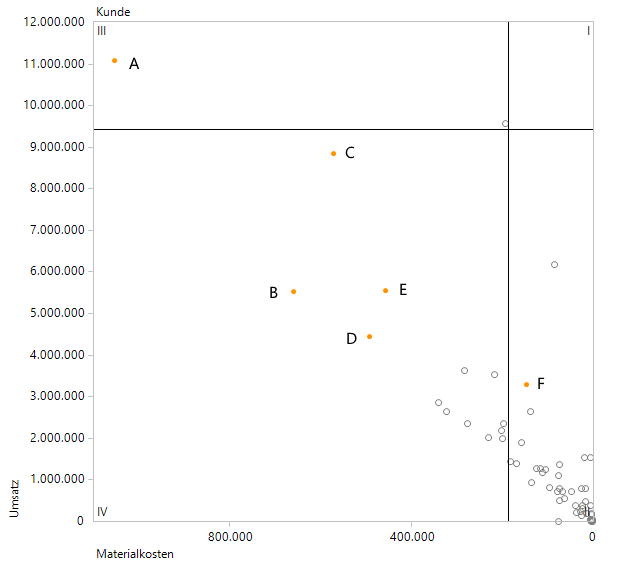
Darstellung ohne die Ausreißer
Die zwei nun verschwundenen Ausreißer sind aus dem Blick, aber nicht aus dem Sinn: Wird im Editiermodus über das rechts aufrufbare Menu eine virtuelle Hierarchie mit den vier Quadranten generiert, so werden die beiden versteckten Objekte weiterhin unterhalb des ihnen zugeordneten Quadranten III einsortiert.
Alternativ könnte man auch einen „hartkodierten“ Filter setzen: Ein Ausreißer sei gegeben, wenn die Materialkosten über 1.2 Mio. liegen oder der Umsatz über 12 Mio. beträgt:
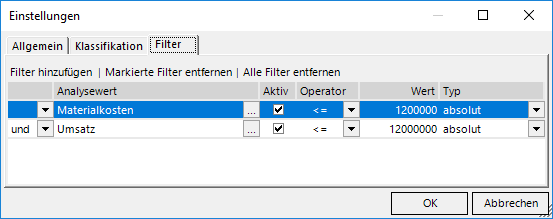
Große Werte werden ausgefiltert
Optisch gibt es bei der Lage der Objekte nun keinen Unterschied zur letzten Grafik zu sehen:
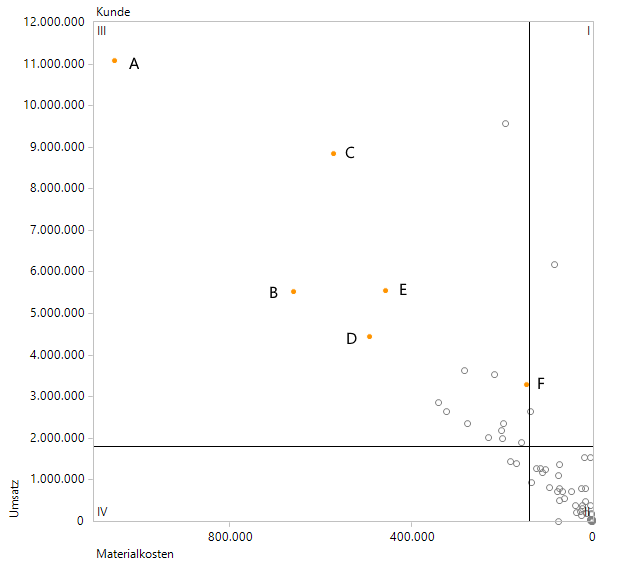
Unveränderte Lage der Objekte bei einem hartkodierten Filter
Ein paar feine Unterschiede sind nun aber doch zu erkennen: Das Fadenkreuzzentrum wird standardmäßig auf die Mittelwerte der beiden Kennzahlen gesetzt; bei der hartkodierten Variante werden nun zur Ermittlung der Mittelwerte nur noch die 59 Objekte berücksichtigt, die den Filter passiert haben, und das Zentrum bewegt sich nach rechts unten.
Einen zweiten Unterschied sieht man, wenn eine virtuelle Hierarchie erstellt wird: Die ausgefilterten zwei Kunden landen nun nicht mehr im Quadranten III, sondern in einer eigens zur Verfügung gestellten Klasse „Gefilterte Elemente“.
Die bisherigen Zahlen seien aggregierte Werte eines ganzen Jahres. Was passiert, wenn die Sicht auf eine Woche eingestellt wird?
Da die Filter nicht mehr greifen, da nun die auftretenden Werte deutlich kleiner sind, befindet man sich wieder im Dilemma, das anfangs geschildert wurde:
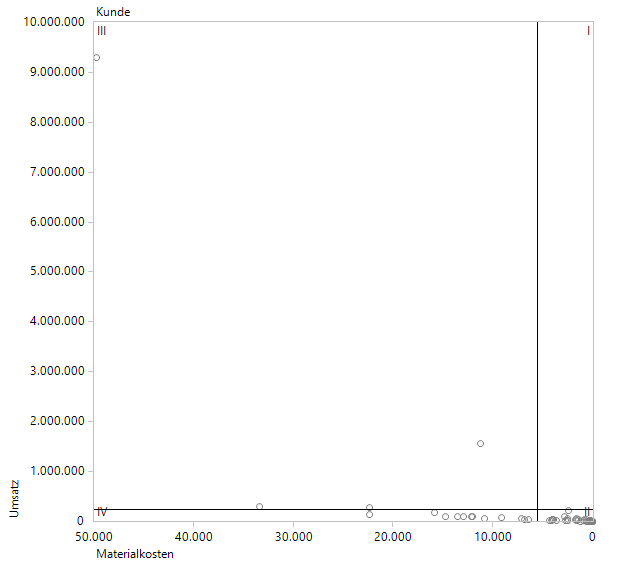
Keine effektive Filterung bei Wochenwerten
Mit seinen 9.3 Millionen Umsatz und den ca. 50.000 Euro Materialkosten bleibt der Ausreißer-Kunde unterhalb der Schwellwerte und wird deshalb weiterhin angezeigt.
Es ist aber häufig durchaus möglich, einen dynamischen Filter zu bauen! Hierzu benutzen wir die in DeltaMaster vorhandene Möglichkeit (über univariate statistische Analysewerte!), Median und Quartile einer Kennzahl wie etwa Umsatz auf der Kundenebene zu ermitteln.
Nun lässt sich ein Schwellwert S erstellen, der beispielsweise 10-mal so weit vom Median entfernt ist wie das 75%-Quartil: S = Median + 10 * (Q75 – Median)
Diesen Schwellwert verknüpfen wir jeweils in einem Analyse-Filterwert mit dem all-Element der Kundendimension (oder dem Hierarchieelement der Kundendimension, das die aktuelle Kundenauswahl der Portfolioanalyse bestimmt). Dieser Schritt ist notwendig, damit Quartile und Median aller Kunden und somit der Schwellwert auch bei der Iteration über die Kunden innerhalb der Portfolioanalyse bekannt sind.
In Gestalt einer weiteren Kennzahl befördern wir die Differenz eines Umsatzes zu diesem Schwellwert in den Filter und lassen einen Umsatzwert nur durch, wenn die Differenz negativ ist, der Umsatzwert also unterhalb des Schwellwerts liegt. Bei den Materialkosten verfahren wir analog. Ein solchermaßen definierter dynamischer Filter würde bei der Wochendarstellung das folgende Bild ergeben:
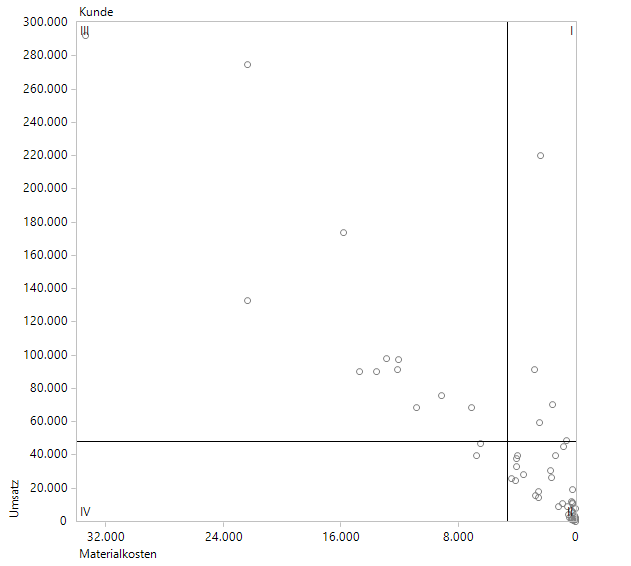
Effektive Filterung mit einem dynamischen Filter auf den Wochenwerten
Hier sind die beiden Kunden mit extrem großen Werten automatisch ausgefiltert worden, um die Lage der nachfolgenden Kunden besser einschätzen zu können.
Dieser dynamische Filter funktioniert aber auch ohne Anpassungen beim Jahresüberblick:
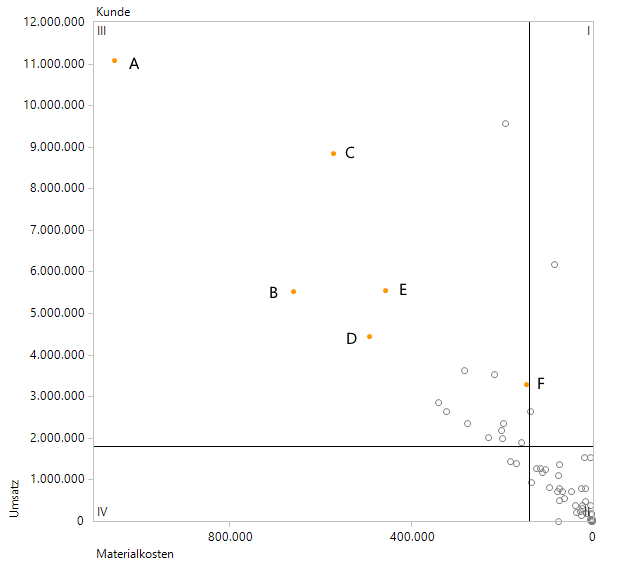
Effektive Filterung mit einem dynamischen Filter auf den Jahreswerten
Das erzeugte Bild bei diesem dynamischen Filter ist absolut identisch mit der Portfolioanalyse, die weiter oben im hartkodierten Fall generiert wurde.
Bei den bisherigen Ansätzen mussten wir jeweils Kompromisse eingehen: Entweder war die Grafik nicht übersichtlich oder es waren einige Kunden nicht mehr abgebildet und/oder die erzeugte virtuelle Hierarchie enthielt die Ausreißer nicht mehr im passenden Quadranten.
Es gibt eine Idee, doch noch viele Anforderungen unter einen Hut zu bringen.
Dazu transformieren wir die Achsen nichtlinear, sodass die großen Werte gedrängter erscheinen und die kleineren Werte auseinandergezogen werden. Die Transformation ist monoton: Befindet sich ein Objekt A links und oberhalb von einem Objekt B, so wird dies auch nach der Transformation der Fall sein.
Die Menge der Elemente, die jeweils einem Quadranten zugeordnet werden, bleibt dabei somit auch unverändert.
Um den Platz optimal zu nutzen, wird der Median einer Kennzahl jeweils auf die Mitte der zugehörigen Achse transformiert. So erreicht man, dass sich jeweils ungefähr 50 Prozent der Daten in der unteren Hälfte (bzw. oberen Hälfte) und gleichzeitig 50 % der Daten in der linken (bzw. rechten Hälfte) des Diagramms befinden.
Das Fadenkreuzzentrum wird in der gleichen Art und Weise mittransformiert. Es wird somit nicht durch die Mittelwerte der transformierten Werte bestimmt, sondern ergibt sich als Ergebnis der Transformation, angewandt auf das ursprüngliche Fadenkreuzzentrum:
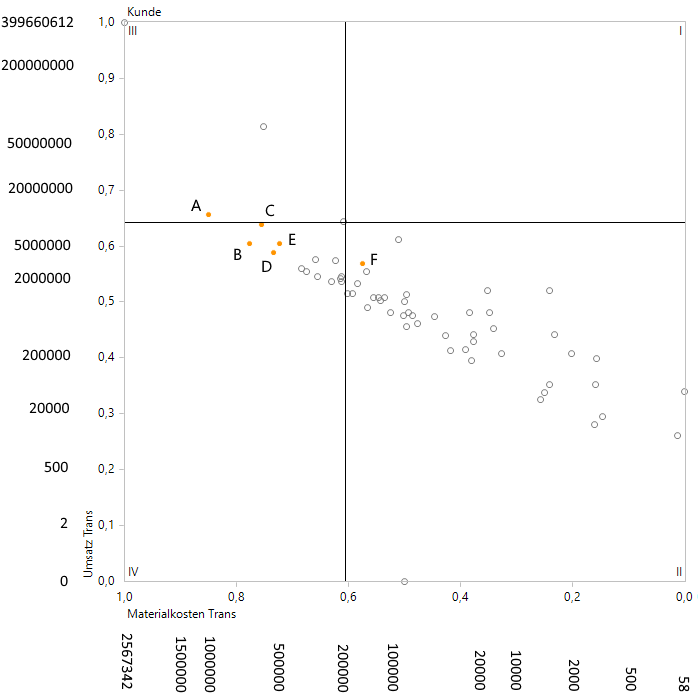
Eine Portfolioanalyse mit nichtlinearen Achsen
Bei einer solchen Darstellung werden die Punkte auseinandergezogen und sind somit leichter mit Mouseover identifizierbar. Eine erzeugte virtuelle Hierarchie bleibt unverändert zur Ausgangssituation. Relative Anordnungen wie „oberhalb/unterhalb von“ bzw. „links/rechts von“ bleiben unter dieser Transformation erhalten.
Hier haben wir an die nichtlinear skalierten Achsen die passenden Label gesetzt, die den Platz der hier noch sichtbaren Werte zwischen 0 und 1 einnehmen würden. Ein kleiner Wermutstropfen wird sichtbar, der uns mit dieser nichtlinearen Transformation eingeschenkt wird: Der umsatzstärkste Kunde mit ca. 400 Mio. wird in unserem Beispiel nur noch in etwa der doppelten Höhe eines Kunden mit 1 Mio. Umsatz angesiedelt. Es ist also schwieriger geworden, die absoluten Beträge zu vergleichen.
