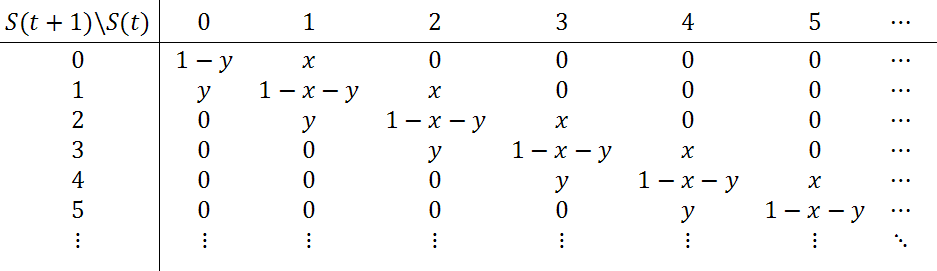Ob im Callcenter oder an der Kasse – wirklich gerne wartet hier keiner. Wie kommt es eigentlich, dass sich vermeintlich aus dem Nichts Schlangen aufbauen? Könnte man diese sicher verhindern? Nutzen wir doch einfach die Wartezeit, um ein wenig über diese Fragen nachzudenken!
Nehmen wir einmal als einfaches Beispiel die Anzahl der Briefanfragen her, die in einem Unternehmen von einem einzigen Mitarbeiter beantwortet werden. Jeden Morgen um die gleiche Zeit trifft pünktlich die Post ein, die eine gewisse Anzahl X(t) von neuen Anfragen an diesem Tag t beinhaltet. Der Mitarbeiter kann maximal Y(t) Anfragen an diesem Tag beantworten. Sei S(t) der Stand von offenen Anfragen am Ende des Tags t, dann gilt: S(t) = S(t-1) + X(t) – Y(t). Sollte sich nach dieser Formel ein negativer Wert ergeben, wird S(t) = 0 gesetzt, d. h. der Mitarbeiter hatte den Stapel abgearbeitet und besaß freie Ressourcen für andere Aufgaben.
Im einfachsten Szenario sind alle Größen deterministisch: Jeden Tag treffen x Briefe ein und maximal y Anfragen werden beantwortet. Es ist offensichtlich, dass ein etwaiger Stapel genau dann abgebaut wird bzw. erst gar nicht entsteht, wenn y > x ist. Sollte y = x sein, werden die jeden Tag eintreffenden Anfragen auch beantwortet. Reicht die Kapazität nicht, d. h. y < x, bleiben pro Tag d = x – y unbeantwortete Anfragen übrig, die sich im Laufe der Zeit zu S(t) = t * d anhäufen. Beim deterministischen Fall können sich somit keine überraschenden Schlangen bzw. hier Stapel aufbauen.
Spannender wird es nur, wenn wir zufällige Streuungen zulassen. Nehmen wir an, dass pro Tag genau eine Anfrage bearbeitet und beantwortet werden kann, aber auf der Eingangsseite 0, 1 oder 2 Anfragen eintreffen. Jeder dieser Werte besitze die Wahrscheinlichkeit 1/3. Im Mittel trifft also eine Anfrage ein und genau eine Anfrage wird beantwortet – da sollte also nichts anbrennen können.
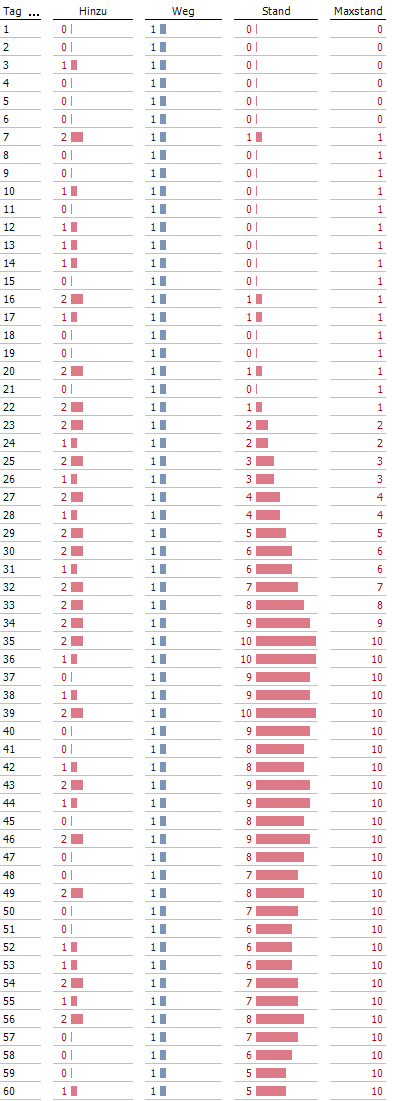
Mögliche Entwicklung mit gleich wahrscheinlichen Eingängen 0, 1 oder 2
Die Grafik – die zufälligen Werte dieser Simulation wurden übrigens direkt in DeltaMaster erzeugt (-> mögliches Thema eines zukünftigen Blogs) – belehrt uns eines Besseren: Es können sich durchaus Tage mit zwei Eingängen häufen und der Stapel der unbearbeiteten Anfragen wächst überraschend hoch – mit den Konsequenzen, dass zeitweise bis zu zehn Anfragen unbearbeitet blieben. Dies bedeutet gleichzeitig, dass bei Annahme von FIFO manche Personen auch 11 Arbeitstage auf die Beantwortung haben warten müssen – wie etwa die Person, deren Antrag an Tag 36 eingetroffen ist. Zunächst gehen die 10 Anträge des Stapels vor und dann dauert es einen weiteren Tag, bis der ausgewählte Antrag selbst bearbeitet wurde.
Wie wir gleich sehen werden, handelt es sich hier nicht um einen unglücklichen Verlauf, sondern um eine prinzipiell vorhandene Schwäche. In diesem Beispiel tendiert der Stapel dazu, immer weiter anzuwachsen und der Anteil der Tage, an denen der Schreibtisch wirklich leergeräumt wird, ist verschwindend gering.
Auch ohne Formel ist klar, dass bei der vorliegenden Konstellation keine Tendenz vorliegt, einen bestehenden Stapel abzubauen. D. h. eine einzelne Person wird nach längerer Zeit beinahe immer einen Antrag auf dem Tisch liegen haben, es aber immer seltener schaffen, Wartezeiten bei den Kunden zu vermeiden. Diese Konstellation dürfte den Kunden nicht gefallen, obwohl aus Sicht des Arbeitgebers der Bearbeiter gut beschäftigt wird.
Wenn eine Person für die Abarbeitung nicht ausreicht, sollte dann eine zweite eingestellt werden? Da maximal zwei Anfragen pro Tag eintreffen können, wäre dann am Abend auf jeden Fall jede Anfrage bearbeitet. Aus Kundensicht ist dies zwar optimal, aber nun wären die beiden Angestellten nur an einem Drittel aller Tage durchgehend beschäftigt, an einem weiteren Drittel arbeitet nur einer und am letzten Drittel keiner der beiden an irgendwelchen Anträgen.
Bei hoher angenommener Flexibiltät wäre es möglich, dass eine zweite Person nur bei Bedarf mithilft und zwar immer dann, wenn zwei Anträge anfallen. Hier wären dann die Kunden auch zufrieden, da keine Wartezeiten entstehen.
Wir wollen nun unser Szenario in der Form erweitern, dass wir bei den Wahrscheinlichkeiten annehmen, dass 0 Anträge mit der Wahrscheinlichkeit x, der Fall von 2 Anträgen mit y und der „neutrale“ Fall eines Antrags mit der Restwahrscheinlichkeit 1 – x – y auftreten. Hier soll x > y gelten, sodass der Abbau des Stapels mit einer höheren Wahrscheinlichkeit vorkommt als der Aufbau.
Hat der Stapel der unbearbeiteten Anfragen eine Höhe S(t) = k (es gelte k > 0) erreicht, so ist die erwartete Höhe des Stapels am Folgetag E(S(t+1)|S(t)=k) = x * (k-1) + (1 – x – y) * k + y * (k+1) = k – (x – y) und dieser Ausdruck ist unter der Annahme „x > y“ kleiner als k. Reicht in diesem Szenario also eine Person aus?
Wir wollen versuchen, mehr über erwartete Stapelhöhen und über Wahrscheinlichkeiten, den Stapel vollständig abzubauen, herauszufinden. Wir nehmen wie in der Grafik an, dass anfangs keine Anfragen auf dem Stapel vorliegen – dies drücken wir mit S(0) = 0 aus. Es lassen sich Übergangswahrscheinlichkeiten zwischen den Endbeständen S(t) und S(t+1) aufeinanderfolgender Tage wie in der folgenden Tabelle (Klicken Sie bitte auf die Grafik für eine vergrößerte Darstellung!) angeben:
Wir haben es hier mit einer Markov-Kette zu tun. Man kann durch Lösung von bestimmten auftretenden Differenzengleichungen zeigen, dass nach einer gewissen längeren Anlaufphase kleine Stapelhöhen k an einem zufällig ausgewählten Tage etwa mit den folgenden Wahrscheinlichkeiten auftauchen:
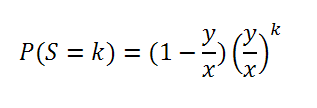
Wahrscheinlichkeit der Stapelhöhe k
Diese Formel ergibt sich nur, wenn y < x ist. Es handelt sich um die Wahrscheinlichkeitsfunktion einer geometrischen Verteilung. Auffällig ist hier auch, dass für die sich langfristig einstellende stationäre Verteilung der möglichen Stapelhöhen nur das Verhältnis der beiden Wahrscheinlichkeiten eine Rolle spielt.
Besonders interessant ist die Wahrscheinlichkeit, an einem zufällig ausgewählten Tag nach ein paar Wochen abends einen abgearbeiteten Stapel zu sehen: Diese beträgt 1 – y/x. Dies bedeutet, dass je dichter y an x heranreicht, desto seltener der Stapel komplett abgearbeitet wird.
Strebt y immer dichter gegen x, wird diese Wahrscheinlichkeit P(S=0) immer kleiner und verschwindet allmählich. Es ist also kein Wunder, dass sich in unserem nicht von der Formel abgedeckten Grenzfall von oben mit x = y = 1/3 der Stapel nicht auflösen will. Soll beispielsweise mit mindestens 84 % Wahrscheinlichkeit die erlaubte Stapelhöhe am Abend maximal 1 betragen, so ist dies auf lange Sicht nur möglich, wenn y <= 0.4 * x ist. Treten also 0 Anträge mit Wahrscheinlichkeit 0.4, 1 Antrag mit 0.5 und 2 Anträge mit 0.1 auf, so ist diese Bedingung erfüllt.
Weiterhin lässt sich die erwartete Stapelhöhe auf lange Sicht berechnen, sie beträgt E(S) = y/(x-y). Auch hier sieht man, dass die erwartete Stapelhöhe beliebig hoch wird, wenn sich y dem Wert von x nähert. Möchte man den Fall E(S)=0 erzwingen, so ist dies nur möglich, wenn niemals 2 Anträge eintreffen. Eine erwartete Stapelhöhe von 1 tritt ein, wenn x doppelt so groß ist wie y.
Auch die Varianz lässt sich einfach berechnen, diese beträgt Var(S) = x*y/(x-y)^2.
Abschließend wollen wir in der Simulation die Ergebnisse der Theorie nachvollziehen. Wir nehmen an, dass 0 Anträge mit Wahrscheinlichkeit 0.4 und 1 und 2 Anträge jeweils mit 0.3 auftreten. Die Theorie sagt, dass nach der Einschwingphase an einem zufällig ausgewählten Tag ein abgebauter Stapel der Höhe 0 mit Wahrscheinlichkeit 1-0.3/0.4 = 0.25 auftritt. Die erwartete Stapelhöhe beträgt E(S) = 0.3/0.1 = 3 und die Varianz Var(S) = 0.4*0.3 / 0.01 = 12. Für die Simulation starten wir 10.000 Durchläufe, deren mittlere Stapelhöhe am Tag t wir in der folgenden Grafik abgebildet haben. Zusätzlich ist der erste dieser Durchläufe dargestellt.
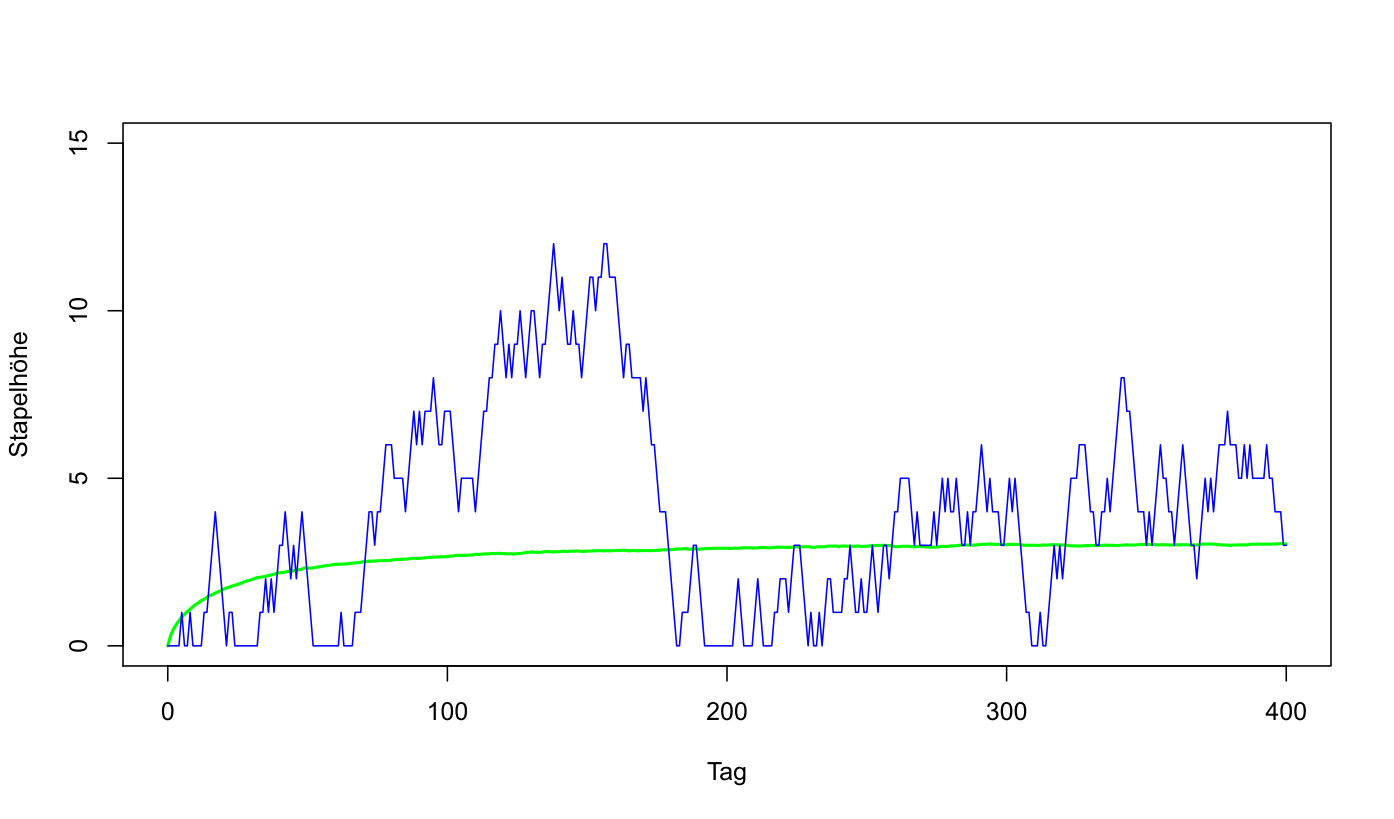
Mittlere Stapelhöhe aller 10.000 Durchläufe (grün) und erster Durchlauf (blau)
Wir sehen, dass etwa 300 Tage vergehen, bis sich das System einschwingt und die oben genannten Formeln angewendet werden können. Wie der ausgewählte Durchlauf zeigt, kann die Stapelhöhe durchaus anwachsen, in diesem Beispiel auf 12 Anträge. Der maximale Wert aller 10.000 Durchläufe betrug übrigens 31.
Wir schauen jeweils auf die Stapelhöhe am Ende des Tags 400. Der mittlere Wert betrug 3.04 – dies ist dicht am theoretischen Wert 3 und die Stichprobenvarianz der Stapelhöhen 12.4 anstelle der theoretischen 12. In 24.6 % aller Durchläufe war an Tag 400 der Stapel leer – vorausgesagt hatten wir 25 %. In 18.6 % der Fälle hatte der Stapel eine Höhe von 1 – die Theorie sagt 18.8 %. Selbst die theoretische Wahrscheinlichkeit für Stapel der Höhe 10 passt mit 0.0141 sehr gut – der empirische Wert betrug ebenfalls 1.41 %. Das folgende Histogramm zeigt die tatsächlichen Häufigkeiten an Tag 400 und die asymptotisch erwarteten Werte (grün) noch einmal zusammen:
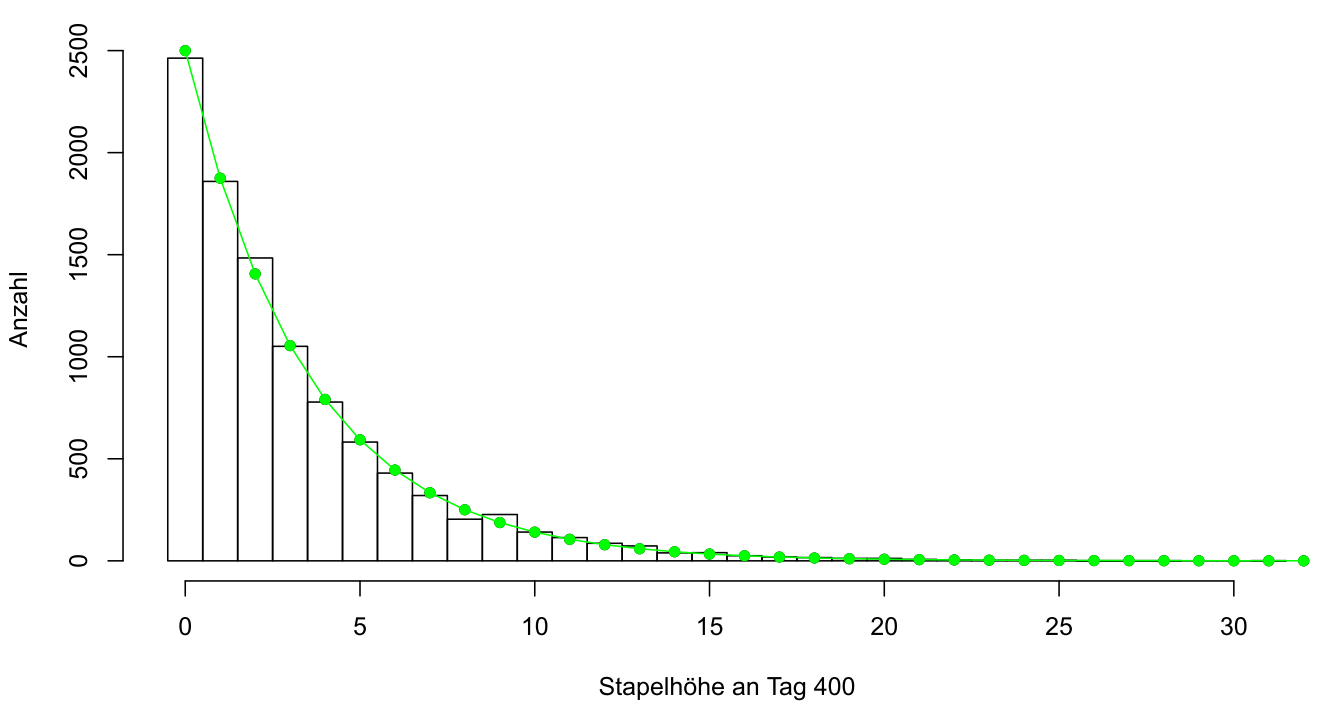
Histogramm der Stapelhöhen am Tag 400 und Approximation (grün)
Solange y>0 ist, können mit positiver Wahrscheinlichkeit auf lange Sicht beliebig hohe Stapel auftreten – die Bedingung y < x stellt aber sicher, dass der Stapel aber auch immer wieder abgebaut wird, auch wenn es einmal länger dauern könnte. Mit welcher Wahrscheinlichkeit ist ein Sachbearbeiter an einem Tag unbeschäftigt? Dies passiert, wenn der Stapel abgebaut ist und am nächsten Tag keine Anfrage eintrifft, also mit Wahrscheinlichkeit (1 – y/x) * x, hier im Beispiel somit mit 10 %.
Schon in diesem relativ einfachen Fall ist gutes mathematisches Rüstzeug Voraussetzung, um nicht von vermeintlich überraschenden Entwicklungen aus dem Konzept gebracht zu werden. Trotzdem haben wir das Gebiet nur an der Oberfläche angekratzt. Erkenntnisse der Warteschlangentheorie können vielfältig eingesetzt werden, sind äußerst interessant, aber auch theoretisch herausfordernd – und ergeben somit eine Konstellation, wie wir sie mögen! Sollte die analytische Bewältigung zu schwierig werden, können Simulationen weiterhelfen.