Als Berater-Frischling kann man sich kaum vorstellen, wie mehr als drei Dimensionen in einen Würfel reinpassen sollten – man kann es sich noch nicht einmal bildlich vorstellen. Falls es dem/der ein oder anderen genauso gehen sollte, haben wir vielleicht eine Lösung parat. Deshalb stellen wir heute mutig den multidimensionalen Modellierungsansatz in Frage und behaupten, dass wir eindimensional auch nicht so schlecht fahren würden!

Jüngst wurden wir mit einem Hilferuf von einem Kollegen konfrontiert, der gern auf einem Bericht die Zeilenachse dynamisch tauschen würde und das am liebsten ohne Flexreport. Als Lösung fällt der eindimensionale Modellierungsansatz ein, den wir einmal in einem Konzeptionspapier eines Kunden gelesen hatten. Damals hielten wir diese Idee noch für vollkommen abwegig und haben sie großspurig vom Tisch gewischt – wir wissen ja schließlich wie man „richtig“ OLAP modelliert. In dem oben genannten Beispiel ist dieser Ansatz aber genau die Lösung für das Problem. Und als netten Nebeneffekt erreicht man auch noch eine immense Performancesteigerung für alle Listen- und Tapeten-Junkies. Also unter dem Strich durchaus vielversprechend. Heute würden wir ernsthaft über den Ansatz nachdenken – und diesen kann man sich wenigstens auch vorstellen.

Der Maniac-OLAP-Ansatz

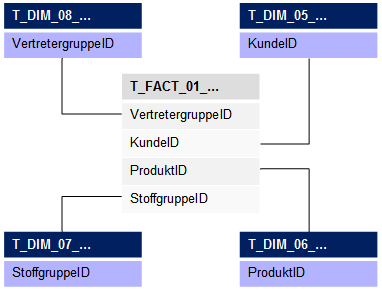
Für den vorliegen Blogbeitrag werden wir unser Chair-Demomodell etwas verbiegen, um den Ansatz schrittweise zu erläutern. Zunächst schauen wir uns den typischen „Lehrbuchansatz“ zur Modellierung von OLAP-Modellen auf Basis eines normalen Snowflake-Schemas an:

Abb. 1: Snowflake-Schema

In einer zentralen Faktentabelle wird pro Analysemerkmal eine Spalte angelegt. Je Merkmalsspalte existiert eine Dimensionstabelle. Soweit nichts Neues. Mit den Dimensionen kann man nun wunderbar analysieren und die Daten durch den Wolf drehen. Das einzige was uns die OLAP-Datenbank übel nimmt, sind umfangreiche Verschachtelungen der Dimensionen, sogenannte Crossjoins. Obendrein lässt sich oben genannte Aufgabenstellung nicht mit diesem „klassischen“ Ansatz lösen. Denn das eigentliche Problem liegt in der Vorabdefinition des Berichtsaufbaus: hier wird quasi festgelegt, welche Dimensionen in den Achsen und welche im Filter liegen. Würden wir nun per MDX die Zeilendimension austauschen, dann passt die Cockpit-Definition nicht mehr zur Abfrage und läuft auf einen Fehler. Somit kann die Lösung eigentlich nur darin liegen, die Zeilendimension eben nicht zu verändern. Und hier kommt die eindimensionale (und eigentlich völlig verrückte) Idee ins Spiel.

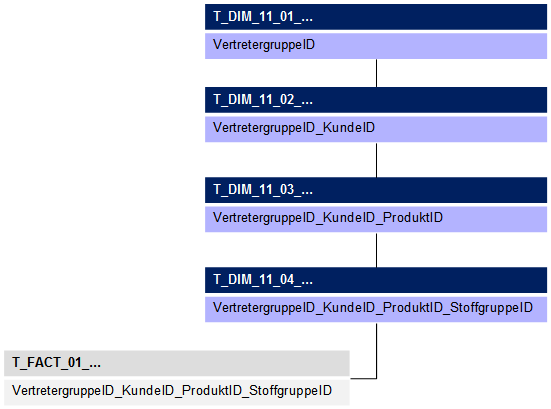
Was müssen wir tun, um mit einer Dimension auszukommen und trotzdem über alle Merkmale auswerten zu können? Eben alle Merkmale in eine Dimension packen! Was aber tun wir, wenn ein Produkt von mehreren Kunden gekauft wird? Wir wenden den alten OLAP-Modellierer-Haudegen-Trick an und machen die Elemente durch Verkettung künstlich eindeutig. Der Profi nennt das „Konkatenation“. Und das machen wir nicht nur mit zwei Dimensionen, sondern mit allen Dimensionen, die wir im Schaubild aufgezeigt haben. Die verschiedenen Dimensionen bilden dann die Ebenen in unserer neuen „Master-Dimension“. Je tiefer wir in die Dimension abtauchen, desto mehr müssen wir verschachteln. Damit wir aber nicht unter jedem Kunden auch jedes Produkt zeigen müssen, bauen wir die Dimension aus den Fakten auf. Das Ergebnis sieht folgendermaßen aus:

Abb. 2: Modellierungsergebnis

An der Stelle muss ich noch etwas gestehen. Wenn man es ganz genau nimmt, ist das Ergebnis dann aber doch nicht ganz eindimensional. Unsere vier Standarddimensionen (Periode, Periodenansicht, Wertart und Kumulation) haben wir nicht in das Maniac-OLAP-Konzept gepresst und würden dies auch nicht empfehlen. Diese Dimensionen sind zu wichtig für die DeltaMaster-Analysen. Daher bleiben sie separat. Somit haben wir eigentlich ein fünfdimensionales Modell, verrückt ist es trotzdem noch.

Maniac-Analysen

Nun fragt sich der ein oder andere wie man in diesem Modell vernünftig analysieren soll. Und schaut man sich das Ergebnis in DeltaMaster an, sieht es auf den ersten Blick auch wirklich seltsam aus.

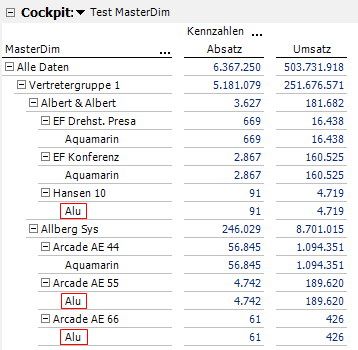Abb. 3: Ergebnis der Auswertung in DeltaMaster

Wir haben zwar schon dafür gesorgt, dass als Anzeigetext nur der Name der jeweiligen Ebene gezeigt wird und nicht der konkatenierte (yeah…) Text. Aber trotz allem ist es mehr als ungewohnt, unsere OLAP-Daten so untereinander zu sehen. Obendrein sehen wir die gleichen Elemente mehrfach. Hier zum Beispiel die Stoffgruppe „Alu“. Wie viel Umsatz „Alu“ in Summe erwirtschaftet hat, bleibt erstmal verborgen.

Lässt man jedoch das Ergebnis ein wenig auf sich wirken, so merkt man, dass uns der Ansatz eine spannende Analyse, die gar nicht so leicht durchzuführen wäre, quasi geschenkt hat. Man sieht mit einem Blick, welche Vertretergruppe welche Kunden an Land gezogen hat und welche Produkte in welchen Stoffgruppen diese Kunden bei uns gekauft haben. Und das sehen wir nicht nur für den in der Sicht ausgewählten Zeitpunkt, sondern auch für die komplette Historie mit dem Kunden. Da die verschachtelte Dimension ja über die Faktendaten aufgebaut wird, ist unter einem Kunden immer jedes Produkt zu sehen, welches der Kunde jemals bei unserem Unternehmen gekauft hat. Hier ein Beispiel bei dem die Sicht auf Dezember 2012 eingestellt ist:

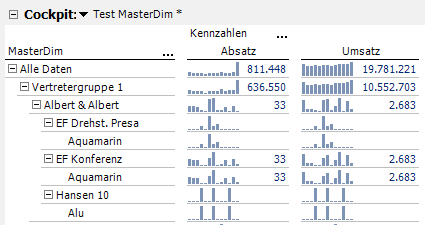Abb. 4: Ergebnis der Auswertung in DeltaMaster II

Wir sehen auf einen Blick, dass der Kunde „Albert & Albert“ irgendwann einmal den „EF Drehstuhl Presa“ in der Stoffgruppe „Aquamarin“ bei uns gekauft hat, sowie den legendären „Hansen 10“ in der Alu-Version (die Sparklines beweisen den früheren Kauf). Eine durchaus spannende Information, insbesondere für den Vertrieb: Warum hat der Kunde das Produkt nicht öfter gekauft? Gibt es hier noch Potenzial?
Die erfahrenen Leser dürfen jetzt kurz darüber nachdenken wie man eine vergleichbare Analyse mit einer normalen Modellierung hinbekommen würde…

Leider sind wir aber noch nicht ganz da wo wir hinwollen. Wie bereits erwähnt, fehlt uns gänzlich die Möglichkeit eine Summenanalyse über einzelne Produkte oder Stoffgruppen durchzuführen. Weiterhin ist eine kreuztabellarische Darstellung (also zum Beispiel die Kunden auf die Zeilen, die Produkte auf die Spalten) noch nicht möglich. Die Lösung für dieses Thema ist aber relativ einfach – quasi eine OLAPpalie (Tschuldigung, das musste sein)!

Also bitte mal kurz grübeln…
…
…na erfolgreich?

Das Zauberwort heißt Attributhierarchie. Normalerweise nutzen wir dieses Konzept, um ein Merkmal nach verschiedenen Hierarchien zu verdichten – also zum Beispiel den Kunden nach Region oder nach Geschlecht. Genau dies können wir uns bei unserer Master-Dimension nun auch zunutze machen. Wir müssen lediglich die „normalen“ Dimensionen (z.B.: All – Land – Region – Gebiet – PLZ – Kunde) als Attributhierarchie an der Master-Dimension aufbauen. Wenn wir diese Attributhierarchien in einen eigenen DisplayFolder legen, ist später kein Unterschied mehr zu einer „normalen“ Dimension erkennbar. Hier ein Vergleich. Links die „normale“ Dimension, rechts die Attributhierarchie über die neue Master-Dimension:

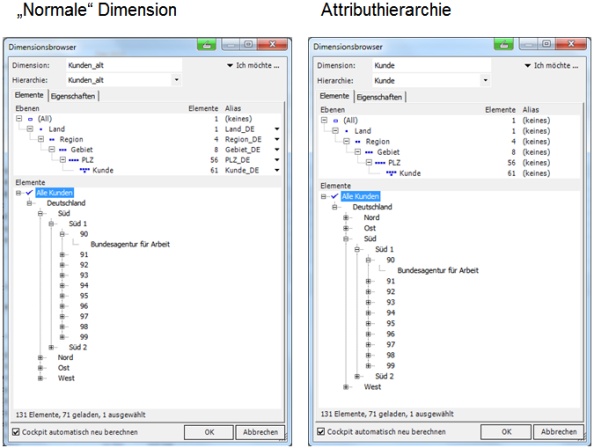Abb. 5: Vergleich normale Dimension vs. Attributhierarchie

Mit diesen als Dimension dargestellten Attributhierarchien können wir jetzt in DeltaMaster kreuztabellieren wie die Weltmeister. Und – wir können sogar Verschachteln und das rasend schnell. Warum? Weil uns hier das AUTOEXISTS-Verhalten der Analysis-Services hilft. Dieses bewirkt, dass eine Filterung einer Attributhierarchie auf alle anderen Attributhierarchien innerhalb derselben Dimension automatisch wirkt. D.h. wenn man ein Produkt auswählt, dann sieht man nur noch die Kunden, die dieses Produkt auch gekauft haben. Und das ohne Leerzeilenunterdrückung! In einem Beispiel haben wir mal unseren Ladenhüter „Arcade AE 77“ ausgewählt:

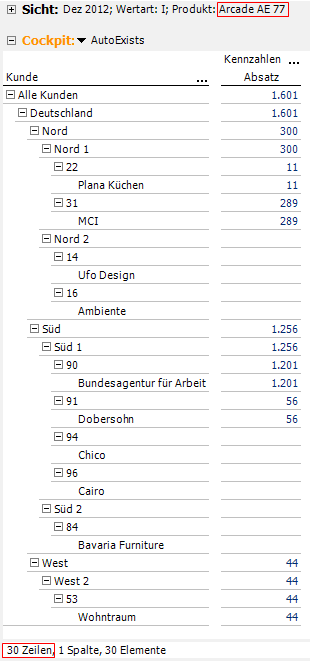Abb. 6: Auswertungsbeispiel anhand des Ladenhüters „Arcade AE 77“

In den Zeilen ist nach wie vor die komplette Kundendimension zur Anzeige ausgewählt. Leerzeilen sind nicht unterdrückt. Trotzdem sieht man nur noch 30 Zeilen mit allen Dimensionszweigen, in denen unser Exot gekauft wurde.

Exakt dieses Verhalten greift dann auch beim Verschachteln. Der OLAP-Server muss also nicht mehr wie beim multidimensionalen Ansatz erstmal das theoretische Kreuzprodukt aus allen Kunden und allen Produkten bilden, um dann anhand der Daten zu entscheiden welche Kombinationen übrig bleiben. Stattdessen sorgt das AUTOEXISTS-Verhalten dafür, dass wirklich nur die gültigen Kombinationen angezeigt werden. Dies passiert automatisch und quasi ohne Rechenaufwand. Also definitiv das „Killerfeature“ für alle Berichtstapezierer.

Die Lösung für das Problem

Allein die gerade dargestellten Analysemöglichkeiten und die Performancezugewinne sind schon Grund genug über diesen Ansatz nachzudenken. Allerdings kamen wir ja von einer konkreten Fragestellung, die es zu lösen galt. Der Weg zur Lösung ist auch nicht mehr all zu weit. Wir müssen lediglich durch eine Sichteinstellung die Hierarchie der Zeilenachse austauschen. Zum Umschalten haben wir uns eine kleine Hilfsdimension mit Elementen, die den Namen der verschiedenen Dimensionen („Vertretergruppe“, „Kunde“, etc.) tragen, gebaut. Jetzt müssen wir unsere Master-Dimension in der Cockpitdefinition in die Zeilenachse ziehen und dort ein paar Zeilen MDX ergänzen, um zwischen den Hierarchien umzuschalten. Folgendes MDX erledigt den Job für uns:

Damit können wir nun die Zeilenachse mit der Schalterdimension ganz einfach umschalten – und wie durch Geisterhand tauscht sich unsere Zeilendimension aus. Und genau darin liegt ein großer Nutzen dieses Ansatzes: man benötigt lediglich einen Bericht mit einer Spaltendefinition und kann diesen x-fach wiederverwenden. Sogar Drillen ist in den Hierarchien möglich. Der Knaller, oder?

Die Grenzen des Ansatzes

Nach dem euphorischen Höhenflug müssen wir aber doch ein wenig bremsen, bevor wir jetzt alle OLAP-Modelle umbauen. Wie so oft gibt es ein paar Einschränkungen, die zu berücksichtigen sind.
Das eben erwähnte Drillen führt zu einem kleinen Problem. Tauscht man die Zeilenachse aus während die Hierarchie gerade aufgeklappt ist, dann kommt es zu einer Fehlermeldung. Diese verschwindet erst wieder, wenn man zuvor die gesamte Dimension zuklappt. Eventuell lässt sich das Problem noch irgendwie programmatisch in DeltaMaster lösen, aber nach heutigem Stand muss man mit dieser Einschränkung leben.
Weiterhin stellt sich die Frage, wie sich ein solch verrückter Ansatz in einem großen Modell mit vielen Daten anfühlt. Schließlich würde die Master-Dimension riesig werden. Wenn man alle Merkmale in einer Dimension verschachtelt, kommt man mit der Elementanzahl vermutlich sehr schnell in den Bereich von zwei- bis dreistelligen Millionenbereich. Ob dies dann noch schnell ist, können wir aktuell noch nicht beurteilen. Eventuell sollte man dann die verschachtelten Textschlüssel der Master-Dimension durch Integer-Surrogatschlüssel ersetzen. Wir hoffen, dass Praxiserfahrungen folgen.
Obendrein lässt sich der Maniac-OLAP-Ansatz nur in Reporting-Umgebungen anwenden. In Planungsumgebungen steht man vor dem Problem der Neuprodukt- oder Neukundenplanung: (neue) Produkte werden erstmals an (neue) Kunden verkauft und umgekehrt. In einem mehrdimensionalen Modell müsste dafür lediglich eine bis dato noch leere Zelle in der Produkt-Kunden-Matrix ausgefüllt werden. In dem eindimensionalen Modell fehlt jedoch das Dimensionselement in der Masterdimension, weil alle Kombinationen aus den Ist-Daten aufgebaut sind. Und wie jeder BI-Berater weiß, können neue Dimensionselemente nicht „mal eben schnell“ durch den Endanwender angelegt werden.

Maniac-Fazit

Der Ansatz ist trotz der beschriebenen Einschränkungen hochspannend und wir werden ihn bei nächster Gelegenheit zum Einsatz bringen. Die verlockenden Performancevorteile beim Schachteln und die interessanten Analysemöglichkeiten sind es wert ausprobiert zu werden. Zumal sich immer wieder eine kleine Gruppe unverbesserlicher Listen-Junkies findet, die sich nachhaltig beratungsresistent zeigt und hier und da mal die Umsätze aller Kunden mit allen Produkten abfragt. Und das selbstverständlich über alle Vertriebsgesellschaften, Währungen und für die letzten zehn Jahre. Vorwurfsvolle Anrufe bezüglich der langen Laufzeiten inbegriffen. Warum also nicht verrückte Anforderungen mit verrückten Modellierungen beantworten.