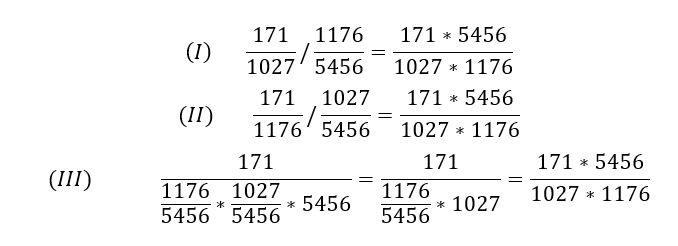Den Bevölkerungsbestand einer Stadt können wir aus verschiedenen Blickwinkeln analysieren. Häufig variieren in den Stadtteilen Altersverteilung, Familienstand, Ausländeranteil und vielleicht sogar die Anteile der Geschlechter. Anhand der Daten von Nürnberg werden wir in diesem Beitrag mögliche Herangehensweisen der Analyse erläutern.
Bevölkerungsbestand in Nürnberg
Für den monatlichen Forschungsblog-Beitrag bin ich ständig auf der Suche nach Datenmaterial. Die Daten sollen zugänglich, aktuell und interessant sein. Meine Lieblingsquelle für multidimensionale Daten ist normalerweise das Statistische Bundesamt.
Ein Kollege gab mir den Tipp, dass auch für Bayern beim open bydata competence center ein Datenportal existiere, das sich das Ziel gesetzt hat, eine Open-Data-Plattform mit qualitativ hochwertigen Daten zu werden. Lobenswert, denn häufig werden in solchen Portalen langweilige und veraltete Datensätze „entsorgt“.
Auch für Nürnberg, wo sich der Hauptsitz von Bissantz & Company befindet, stehen Daten zur Verfügung.
Die Bezirke Nürnbergs mit Einwohnerzahlen
Bei den Daten habe ich mir den Bevölkerungsbestand (Stand 2024) in Nürnberg ausgesucht. Dieser Datensatz ist – wie andere inspizierte Datensätze auch – mit den Bezirken Nürnbergs zwar nur eindimensional, aber es sind doch einige interessante Kennzahlen gegeben, die jeweils durch Projektion der Einwohnerzahl auf eine weitere Dimension erzeugt werden.
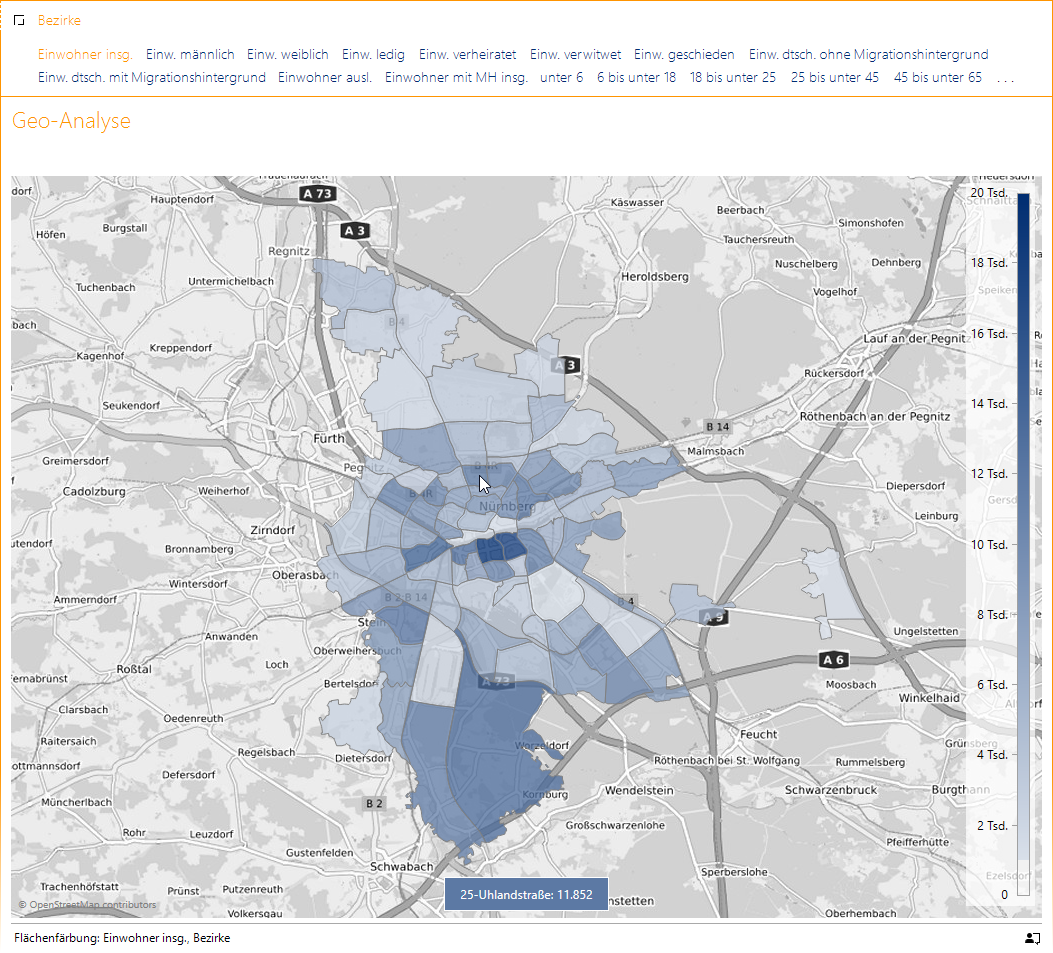
In dieser Geo-Analyse ist wie im Blog-Beitrag Kaltmieten in Deutschland ein Kartendienst von Terrestris eingeblendet. Bei OpenStreetMap (siehe unten bei den Quellen) ist ein Shapefile mit den Bezirken Nürnbergs gegeben. Die Aufbereitung möchte ich in diesem Beitrag nicht in den Vordergrund stellen und verweise auf das prinzipielle Vorgehen wie im Beitrag Kaltmieten in Deutschland.
Nur so viel: Da im Datensatz einige Bezirke aggregiert wurden, in der Karte aber jeder einzelne Bezirk für sich steht, musste ich mit QGIS die zusammengehörigen Polygone der Bezirke verschmelzen. In der Attributtabelle des Shapefiles waren auch Flächenangaben gegeben (man kann sich diese Flächen in QGIS auch mit dem Befehl area selbst errechnen), die ich in Kürze nutzen werde.
Während Fischbach bei der A 9 wenigstens noch mit einer Straße mit dem Stadtgebiet verbunden ist, existiert mit Brunn (ergänzt um Birnthon und Netzstall) eine Exklave, die im Osten oberhalb der A 6 liegt und doch schon ziemlich weit vom Zentrum entfernt ist.
Bevölkerungsbestand: Vorsicht bei absoluten Anzahlen
Im Datensatz ist pro Bezirk die Anzahl der Einwohner insgesamt gegeben. Darüber hinaus liegen die folgenden Differenzierungen der absoluten Anzahlen vor:
Geschlecht: männlich/weiblich
Familienstand: ledig/verheiratet/verwitwet/geschieden
Migrationshintergrund: deutsch/deutsch mit Migrationshintergrund/Ausländer + Kombination (deutsch mit Migrationshintergrund + Ausländer)
Altersgruppe: unter 6, 6 bis unter 18, 18 bis unter 25, 25 bis unter 45, 45 bis unter 65, 65 bis unter 80, ab 80
Es wäre noch schöner gewesen, vor allem für die Anwendung mit der DeltaApp, wenn wir die Anzahlen für die Kombinationen dieser Eigenschaften kennen würden. Dann wären schöne Navigationspfade möglich, um den Bevölkerungsbestand zu sezieren. Mit den gegebenen Daten sehen wir nur die Projektionen des Datenwürfels auf je eine Dimension.
Wenn eine Kennzahl normalerweise proportional mit der Fläche wächst, muss man bei der Interpretation von absoluten Anzahlen aufpassen. Größere Flächen werden dann automatisch dunkler gefärbt, auch wenn die Bevölkerungsdichte in allen Bezirken konstant sein sollte.
Die in der Attributtabelle des Shapefiles gegebenen Flächengrößen der Polygone haben wir exportiert und die aus der CSV-Datei gewonnene Excel-Datei um die Spalte der Flächen ergänzt. Somit kann man nun Quotienten aus Anzahl und Fläche bilden, um den Bevölkerungsbestand pro Quadratkilometer zu erhalten:
Während in Deutschland 2024 ca. 237 Einwohner/qkm lebten, sind es in Nürnberg ca. 2920 Einwohner/qkm:
Die Basisdaten für Nürnberg
Den Unterschied zum Bundesgebiet können wir einfach erklären: Für Deutschland beinhaltet die Gesamtfläche auch Wälder und Felder, aber in Nürnberg sind die angezeigten Flächen fast durchgehend besiedelt. Aber auch in Nürnberg gibt es erhebliche Unterschiede.
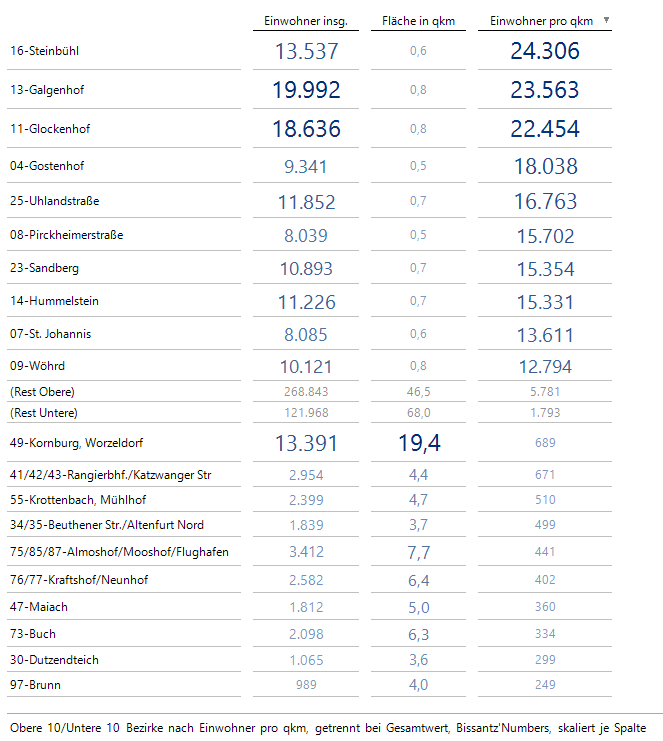
Lassen wir uns in einer Grafischen Tabelle Obere/Untere Einwohner pro qkm nach Anzahl anzeigen, so variieren die Werte von 249 bis 24306 Einwohnern pro qkm:
Obere/Untere nach Anzahl bezüglich Einwohner pro qkm
Wenn Sie die Statuszeile betrachten, sehen Sie, dass die Bissantz’Numbers spaltenskaliert sind, und dass die Grenze zwischen oben und unten automatisch beim Gesamtwert gezogen wird, der wie oben gezeigt bei 2921,9 Einwohnern/qkm liegt. Im Blogbeitrag Trennkriterium für Obere/Untere in Ranking und Navigation aus dem Juli 2024 hatte ich mich ausführlich mit der Trennung zwischen oben und unten beschäftigt.
Bevölkerungsbestand: Einwohner pro qkm in der Geo-Analyse
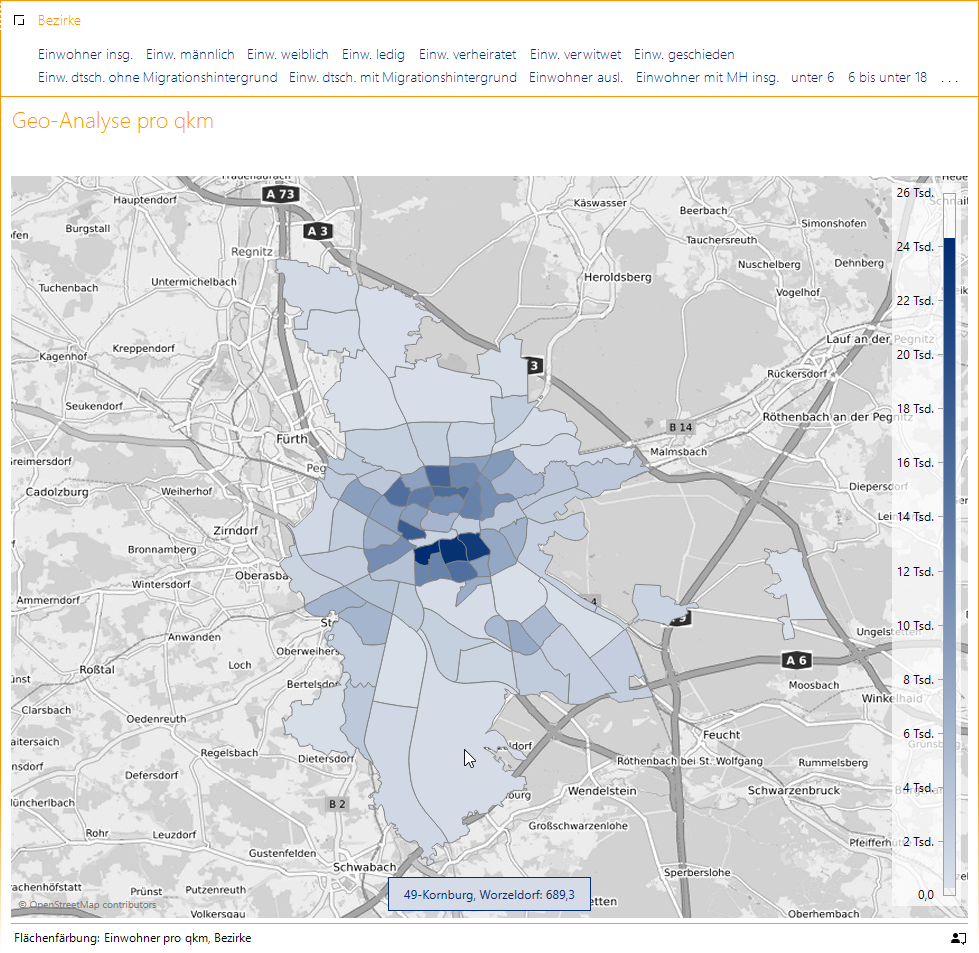
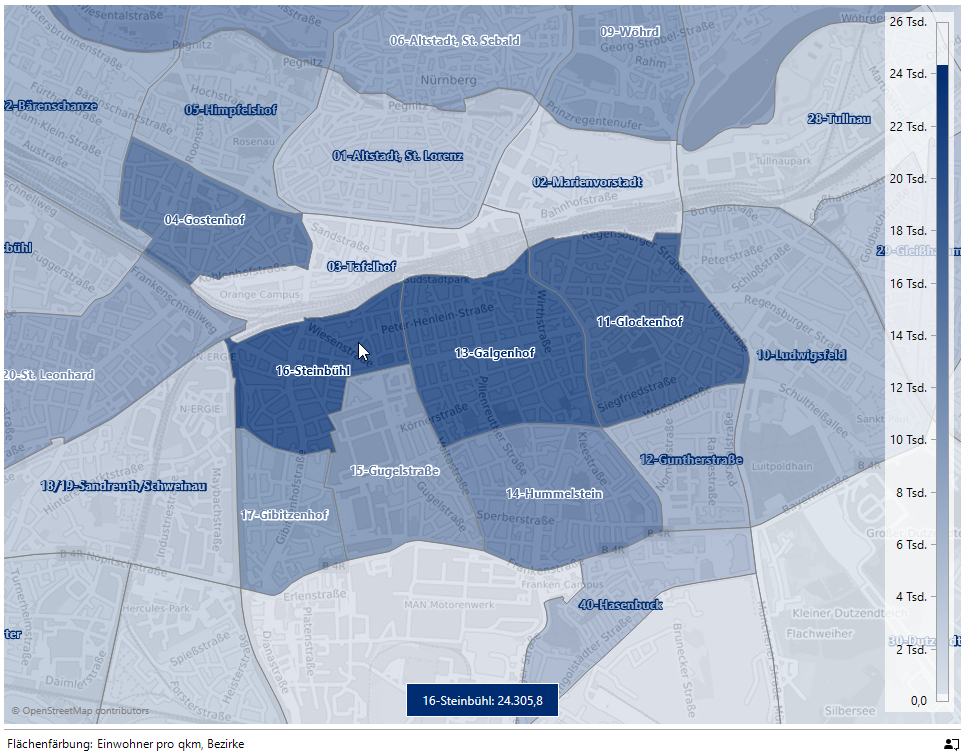
Lassen wir einmal diese Zahlen in der räumlichen Anordnung in der Geo-Analyse auf uns wirken:
Bevölkerungsbestand: Einwohner pro qkm in der Geo-Analyse
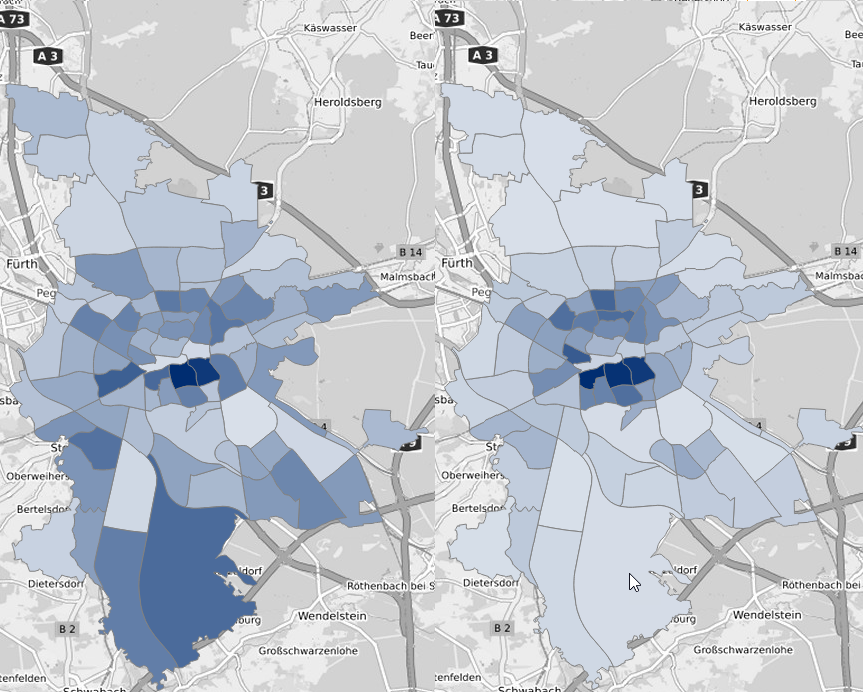
Beispielsweise im südlich gelegenen 49-Kornburg, Worzeldorf ist das dunkle Blau einer hellen Variante gewichen. Besonders deutlich wird der Unterschied im direkten Vergleich:
Bevölkerungsbestand: Absolute Anzahlen vs. Einwohner pro qkm
Wir können einmal in die Karte zoomen und uns per Option im Editieren-Menü die Flächen beschriften lassen:
Einwohner pro qkm in der Südstadt
Die drei höchsten Bevölkerungsdichten finden wir mit 16-Steinbühl, 13-Galgenhof und 11-Glockenhof südlich der Bahnstrecke von West nach Ost aufgereiht.
Bevölkerungsbestand: Analyse der Altersverteilung
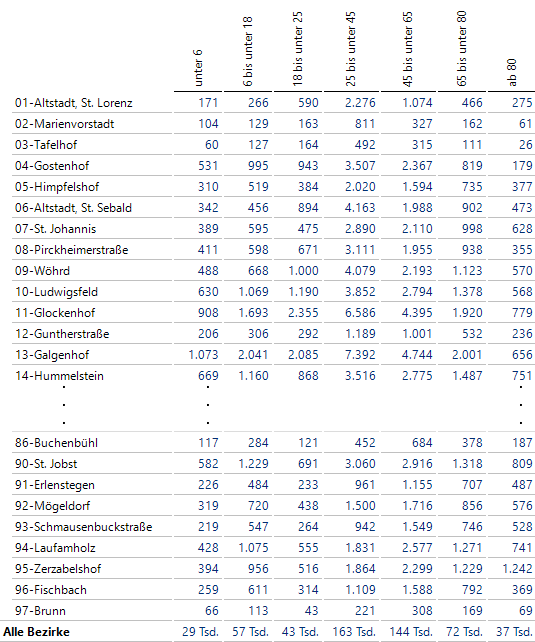
Bei der Analyse der Altersverteilung müssen wir gleich 7 Klassen auf einmal berücksichtigen. Eine verkürzte Ansicht ohne den längeren Mittelteil sieht so aus:
Anzahlen nach Altersstufen in den Bezirken
Bei dieser Grafischen Tabelle habe ich die seit Release 6.6.2 vorhandene Option, Zwischensummenelemente in invertierten Hierarchien optional in Fettschrift darstellen zu können, eingesetzt. Diese Option befindet sich auf dem Reiter Gliederung der Eigenschaften.
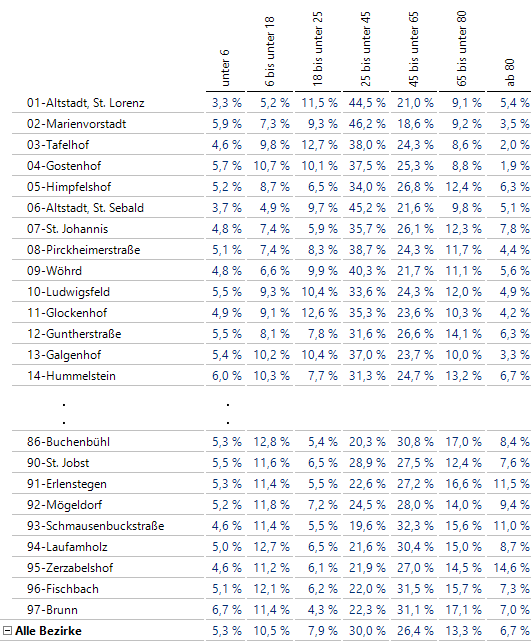
Wir wollen nun auffällige Bezirke identifizieren, die in irgendeiner Form von der Gesamt-Altersverteilung abweichen. Es zählt nur die relative Verteilung über die Altersklassen. Diese können wir über die Darstellungsoption Anteil an Zeilen im Editieren-Menü sehen, ohne dass wir (zunächst) neue Kennzahlen definieren müssen:
Anteile der Altersstufen in den Bezirken
Prozentzahlen ins Verhältnis zum Gesamtanteil setzen
Wir könnten die Prozentzahlen eines Bezirks ins Verhältnis zu den Gesamt-Prozentzahlen setzen. Zum Beispiel ergäbe sich für 97-Brunn für die ersten drei Altersklassen, bei Verwendung aller intern vorhandenen Stellen und anschließender Rundung auf eine Stelle hinter dem Komma:
6,7/5,3=1,3
11,4/10,5=1,1
4,3/7,9=0,6
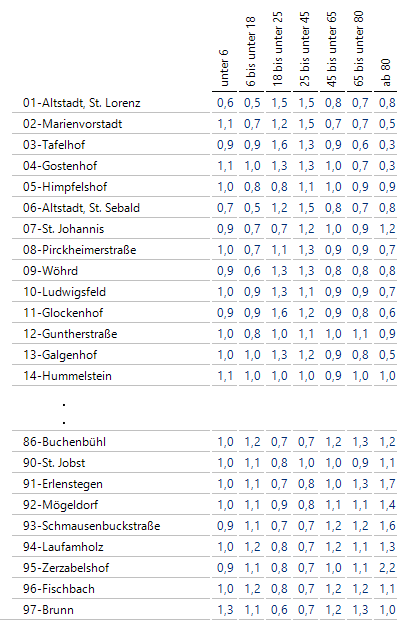
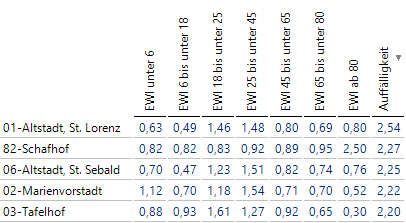
Genau diese Werte berechnet der Erwartungswert-Index. Aktivieren Sie im Editieren-Menü unter Darstellung die Option Erwartungswert-Index, so erhalten Sie eine Tabelle der Verhältnisse im Vergleich zu den Gesamtanteilen:
Erwartungswert-Index der Altersstufen in den Bezirken
Beispielsweise ist in 01-Altstadt, St. Lorenz die mittlere Altersgruppe von 18 bis 45 Jahren besonders stark vertreten, mit 50 Prozent höheren Anteilen, während ältere Menschen und vor allem Kinder und Jugendliche unterrepräsentiert sind. In 14-Hummelstein liegt die Verteilung der Altersklassen sehr nahe an der Gesamtverteilung.
In 97-Brunn kehren sich die Verhältnisse um: Hier ist vor allem die mittlere Altersklasse unterrepräsentiert.
Beim Erwartungswert-index gibt es drei mögliche Interpretationen, die allesamt zum identischen Wert führen.
Exkurs Erwartungswert-Index
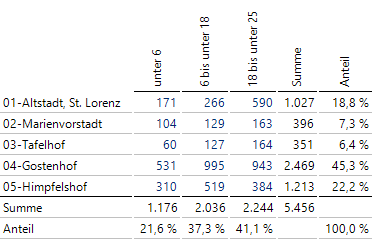
Zur Veranschaulichung arbeiten wir mit einer verkürzten Tabelle mit 5 Bezirken und 3 Altersstufen. Wir blenden über die Option Tabellenaggregationen Summe und Anteil ein:
Vereinfachte Tabelle mit Randsummen und Randanteilen
Schauen wir auf die erste Interpretation wie bereits weiter oben geschildert. 01-Altstadt, St. Lorenz hat in der Altersklasse „unter 6“ einen Anteil von 171/1027. In der Gesamtsumme hat diese Altersklasse einen Anteil von 1176/5456 (= 21,6 %). Teile ich die beiden Anteile durcheinander, ergibt sich der Fall (I):
Drei Interpretationen mit identischem Ergebnis
Bei der zweiten Interpretation schaue ich auf Anteile der Bezirke in einer Altersklasse. Bei der Altersklasse unter 6 befindet sich ein Anteil von 171/1176 im Bezirk 01-Altstadt, St. Lorenz. Insgesamt befinden sich 1027/5456 (= 18,8 %) in diesem Bezirk. Teile ich diese beiden Anteile durcheinander, ergibt sich in (II) das gleiche Ergebnis wie in Fall (I).
Kommen wir zur Interpretation (III), die für den Namen Erwartungswert-Index verantwortlich ist. Angenommen, die beiden Dimensionen Altersklasse und Bezirk wären unabhängig in dem folgenden Sinne:
Eine zufällig ausgewählte Person stamme mit Wahrscheinlichkeit p aus Bezirk A und mit Wahrscheinlichkeit q aus der Altersklasse B. Dann soll die Wahrscheinlichkeit, dass eine zufällig ausgewählte Person gleichzeitig aus Bezirk A und der Altersklasse B stammt, p*q betragen.
Zunächst rechne ich im Nenner bei (III) einen Schätzer für die erwartete Anzahl unter Unabhängigkeit aus. Unter 6 sind 21,6 % (= 1176/5456) und aus dem Bezirk 01-Altstadt, St. Lorenz 18,8 % (= 1027/5456). Dass beide Eigenschaften gleichzeitig zutreffen, kann bei Unabhängigkeit mit dem Produkt 0,216*0,188 ~ 0,04 = 4 % geschätzt werden.
Diesen Prozentsatz multipliziere ich mit 5456 und erhalte die erwartete Anzahl von ca. 221,4. Dann teile ich die tatsächliche Zahl 171 durch die erwartete und es ergibt sich ein Erwartungswert-Index von 0,77. Da nach der Umformung wieder der identische Ausdruck entsteht, passen alle drei Interpretationen zum Erwartungswert-Index.
Weiter mit Erwartungswert-Index
Da der Erwartungswert-Index nur eine Darstellungsvariante einer gegebenen Kreuztabelle ist, ändern sich bei Filtern in den Achsen die sichtbaren Werte für gegebene Bezirke. Um nur die auffälligsten Bezirke sehen zu können, bilde ich die Berechnung der Erwartungswert-Index-Werte für die gesamte Tabelle nach.
Dazu gebrauche ich Filterwerte und Quotienten, wie sie in den Formeln beim Exkurs zu sehen sind. Zusätzlich bilde ich eine Kennzahl Auffälligkeit, die für einen Bezirk über alle Altersklassen die Absolutwerte der Differenzen zwischen Erwartungswert-Index und 1 bildet. Hier kann man sich vergegenwärtigen, dass ein Erwartungswert-Index von 1,46 bedeutet, dass der Anteil dieser Altersklasse in der Zeile um 46 Prozent über dem allgemeinen Anteil dieser Altersklasse liegt.
Ebenso heißt ein Erwartungswert-Index von 0,63, dass der Anteil dieser Altersklasse in der Zeile um 37 % unter dem allgemeinen Anteil dieser Altersklasse liegt.
Meine Kennzahl Auffälligkeit addiert somit die Absolutbeträge dieser relativen Abweichungen.
Der Erwartungswert-Index der Originaltabelle und die Auffälligkeit
An dieser Stelle – der Erwartungswert-Index wurde lange vor den Bissantz’Numbers eingeführt – würde ich auch eher mit der Differenz des Erwartungswert-Index zu 1 arbeiten und die Bissantz’Numbers aktivieren. Nun wird das Auge zu den interessanten Abweichungen gelenkt (zeilenweise Skalierung, da der Wert von 82-Schafhof sehr dominant ist). Die Spalte Auffälligkeit ist von der Skalierung ausgenommen.
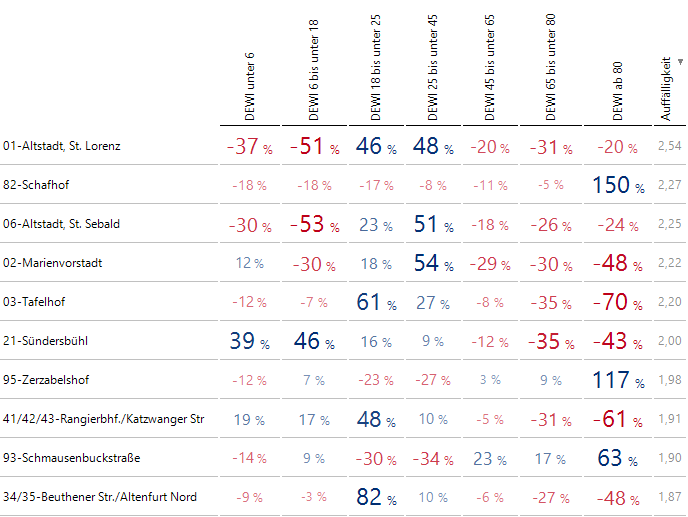
Die Differenzen zu 1 als Prozentzahlen
Die Auffälligkeit, dass in 01-Altstadt, St. Lorenz vor allem die Altersklasse 18 bis 45 stärker vertreten ist und dafür auffällig weniger Kinder und Jugendliche, hatten wir bereits oben erwähnt. 82-Schafhof hat einen deutlich höheren Anteil an über 80 Jahre alten Einwohnern. 06-Altstadt, St. Sebald verhält sich ähnlich wie 01-Altstadt, St. Lorenz, hat aber einen weniger stark erhöhten Anteil bei 18 bis unter 25.
02-Marienvorstadt hat einen starken Block bei 25 bis unter 45 und einen geringen Anteil an Einwohnern ab 80. In 03-Tafelhof finden sich noch weniger Alte, aber dafür ein starker Block bei 18 bis unter 25. Schauen wir noch auf 21-Sundersbühl, das einen sehr jungen Bezirk mit überdurchschnittlich vielen Kindern und Jugendlichen, dafür weniger Älteren ab 45 darstellt.
Mit Bissantz’Numbers und der Farbgebung lassen sich auffällige Zellen und ähnliche Zeilenprofile leicht erkennen.
Korrespondenzanalyse
Die Korrespondenzanalyse stellt ein Verfahren zur Visualisierung von Spalten und Zeilen in Kreuztabellen mit Häufigkeiten dar. Sie ist nicht direkter Bestandteil von DeltaMaster, kann aber in DeltaMaster über Stored Procedures im SQL-Durchgriff integriert werden, wie ich es einmal in einem älteren Artikel Bilder in Berichten: Vorbildlich gelöst! demonstriert hatte. Hierzu müssen die Machine Learning Services auf SQL Server oder einer Azure SQL Managed Instance installiert sein:
Beispiel Korrespondenzanalyse in DeltaMaster
Bei den Einwohneranzahlen nach Altersstufen habe ich auf die Einbindung in DeltaMaster verzichtet und zeige hier das Ergebnis direkt aus R (unter Verwendung des Pakets ca):
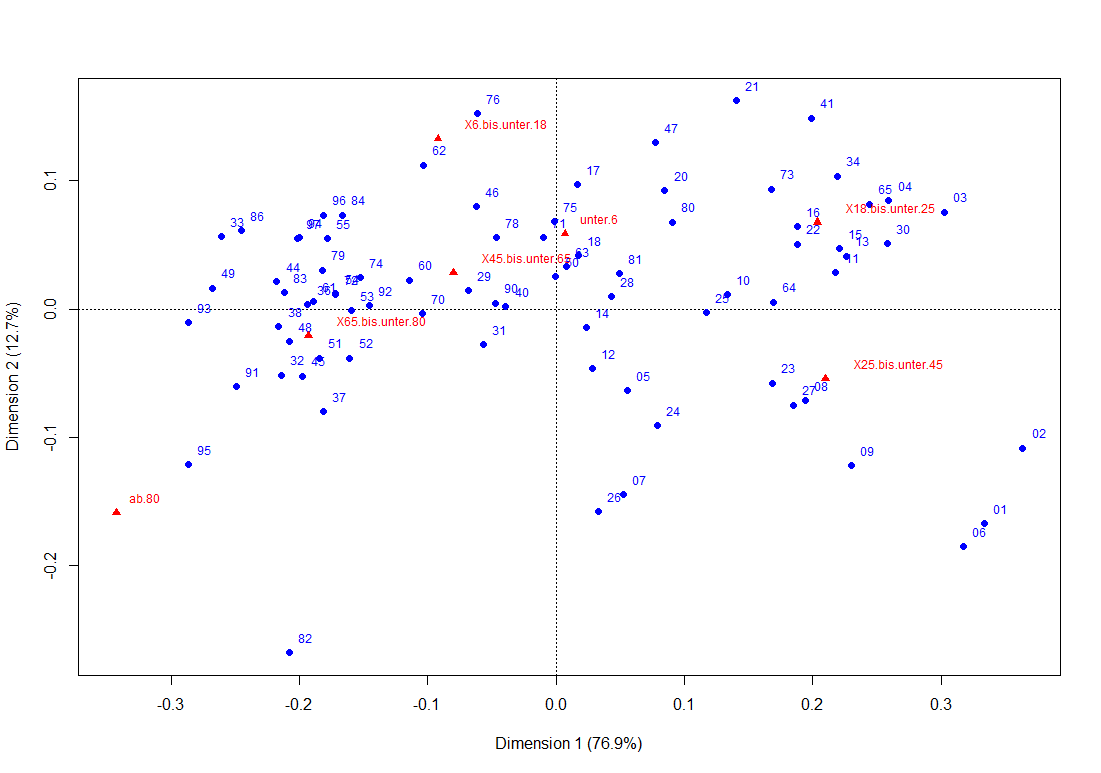
Korrespondenzanalyse in R
Bei der Korrespondenzanalyse werden Zeilenprofile (die relativen Anteile der Altersstufen in einem Bezirk) und die Spaltenprofile (die relativen Anteile der Bezirke in einer Altersstufe) trotz der unterschiedlichen Länge der Vektoren in ein gemeinsames Diagramm projiziert. Ähnliche Spaltenprofile liegen tendenziell dicht zusammen, ebenso wie ähnliche Zeilenprofile.
Aber auch die räumliche Lage von Zeilen- und Spaltenprofilen untereinander spielt eine Rolle: Ein Zeilen- und ein Spaltenprofil liegen tendenziell dichter zusammen, wenn die jeweiligen Anteile im Kreuzungspunkt von Zeile und Spalte größer sind als im allgemeinen Fall. Das gilt vor allem für Punkte am Rand des Diagramms.
Was zeigt nun die Grafik? Links unten sehen wir die Bezirke 82 und 95 relativ nah an der Altersklasse ab 80; das hatten wir eben in der Grafischen Tabelle auch schon gesehen. Rechts unten sind 01 und 06 – wie bereits oben erkannt – ähnlich und in der Nähe der Altersklasse 25 bis unter 45 angesiedelt. 02-Marienvorstadt ist mit seinem hohen Anteil in der Klasse 25 bis unter 45 auch in der Nähe zu finden.
Die Korrespondenzanalyse kann als Ergänzung dienen, um sämtliche Bezirke und ihre Lagen auf einmal zu sehen.
Bevölkerungsbestand: Analyse der Geschlechter
Bei den Geschlechtern männlich/weiblich bietet es sich an, den Frauenanteil in den Bezirken zu berechnen. Der Anteil insgesamt beträgt 50,6 %, aber in den Bezirken variiert der Anteil beträchtlich von 41,5 % bis 54,9 %:
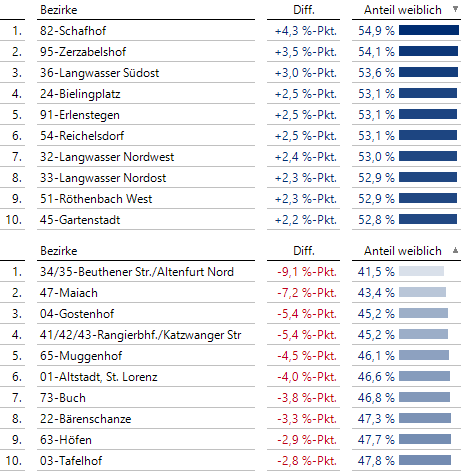
Hohe und niedrige Frauenanteile
Die beiden Bezirke mit den höchsten Frauenanteilen – 82-Schafhof und 95-Zerzabelshof – hatten wir schon als Bezirke mit einem hohen Altenanteil identifiziert. In der Geo-Analyse visualisieren wir die Differenz zum allgemeinen Frauenanteil von 50,6 %:
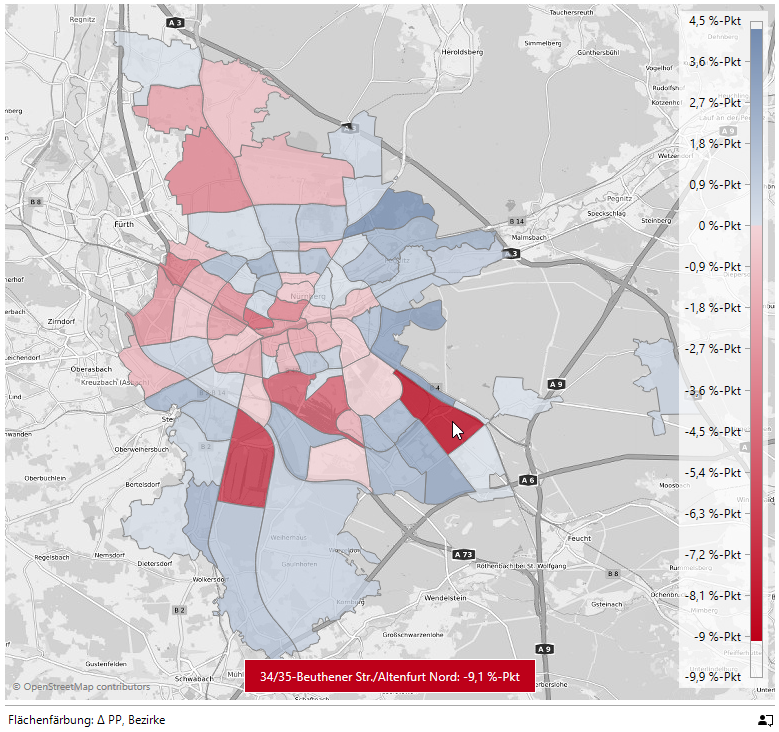
Differenz zum allgemeinen Frauenanteil
Der Mauszeiger befindet sich gerade auf 34/35-Beuthener Str./Altenfurt Nord mit 9,1 %-Punkten unter dem Gesamtwert.
Bevölkerungsbestand: Analyse Ausländeranteil
Wir bilden den Anteil der Einwohner mit Migrationshintergrund (= Deutsche mit Migrationshintergrund + Ausländer) an der Gesamtanzahl der Einwohner:
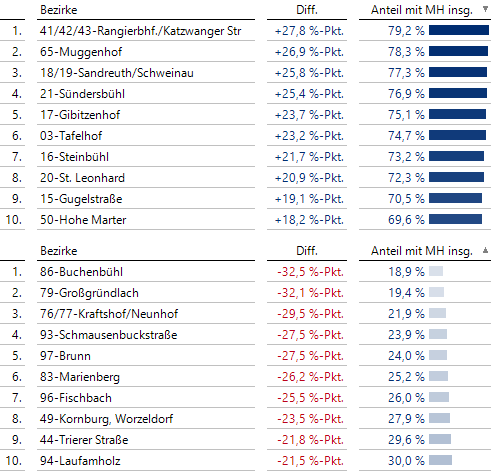
Hohe und niedrige Anteile mit Migrationshintergrund
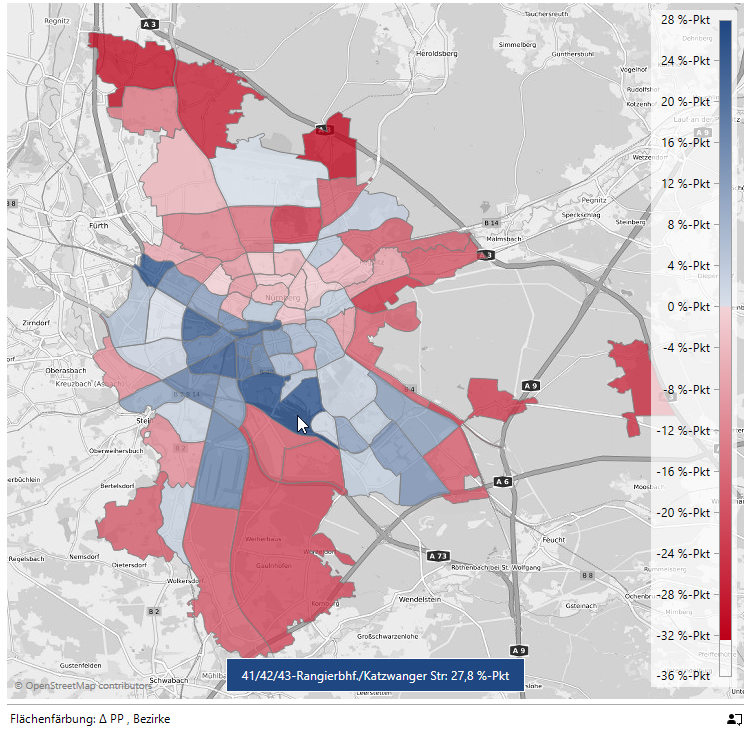
Wie man sieht, variieren hier die Anteile beträchtlich. In der Geoanalyse schauen wir wieder auf die Differenz zum allgemeinen Anteil von 51,4 %:
Differenz zum allgemeinen Anteil mit Migrationshintergrund
In der Analyse ist die Trennung in der Kernstadt nach Nord- und Südstadt gut zu erkennen. Außerdem scheinen sich die Farben gegenüber der Differenz beim Frauenanteil tendenziell umgekehrt zu haben.
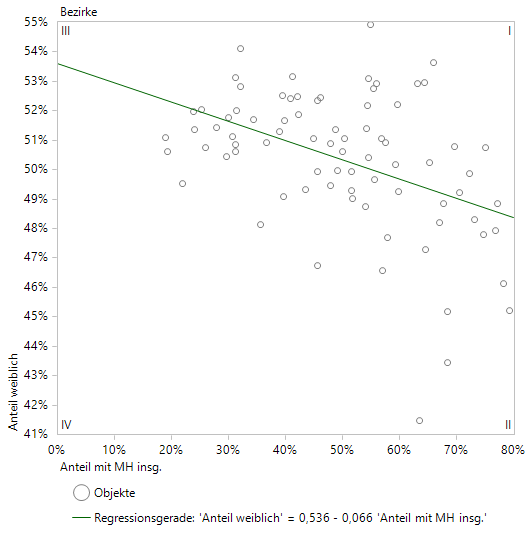
Plotten wir den Anteil der Frauen gegen den Anteil der Einwohner mit Migrationshintergrund, liegt eine sichtbare Korrelation vor. Die in der Portfolioanalyse angepasste Regressionsgerade zeigt fallende Tendenz: je größer der Anteil mit MH insg., desto kleiner der Frauenanteil:
Regressiongerade mit fallender Tendenz
Bevölkerungsbestand: Analyse des Familienstands
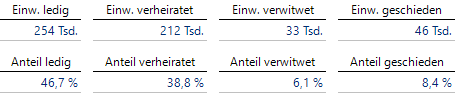
Beim Familienstand gehen wir wieder vor wie bei den Altersklassen. Die allgemeinen Anzahlen und Anteile in Nürnberg sehen wir in der folgenden Grafischen Tabelle:
Anzahlen und Anteile zum Familienstand
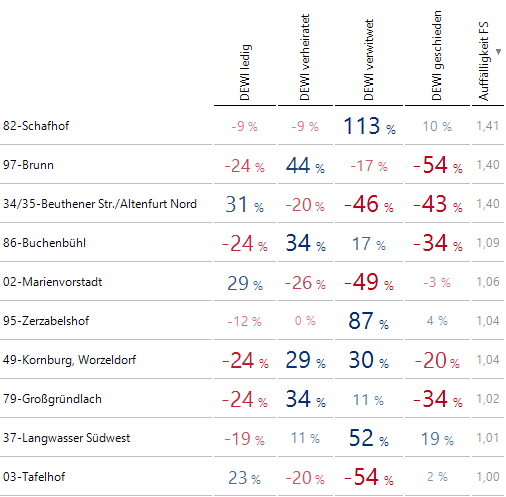
Für die Bezirke berechnen wir die Anteile der vier möglichen Familienstände und setzen sie ins Verhältnis zu den Gesamtanteilen. Danach ziehen wir eine 1 ab und erhalten somit die prozentualen Abweichungen zu den Gesamtanteilen. Dann berechnen wir wieder die Summe der Absolutbeträge der prozentualen Abweichungen und benutzen diese als Auffälligkeitsmaß. Die auffälligsten Bezirke sind gemäß diesem Maß die folgenden:
Auffälligkeiten im Bevölkerungsbestand beim Familienstand
82-Schafhof, das bereits durch hohes Alter aufgefallen ist, zeigt auch einen erhöhten Anteil an verwitweten Personen. In 97-Brunn (die Exklave außerhalb von Nürnberg) ist Scheidung weniger ein Thema. In Bezirk 34 findet man unter anderem einen erhöhten Anteil an ledigen Personen.
Bevölkerungszustand mit Multiples
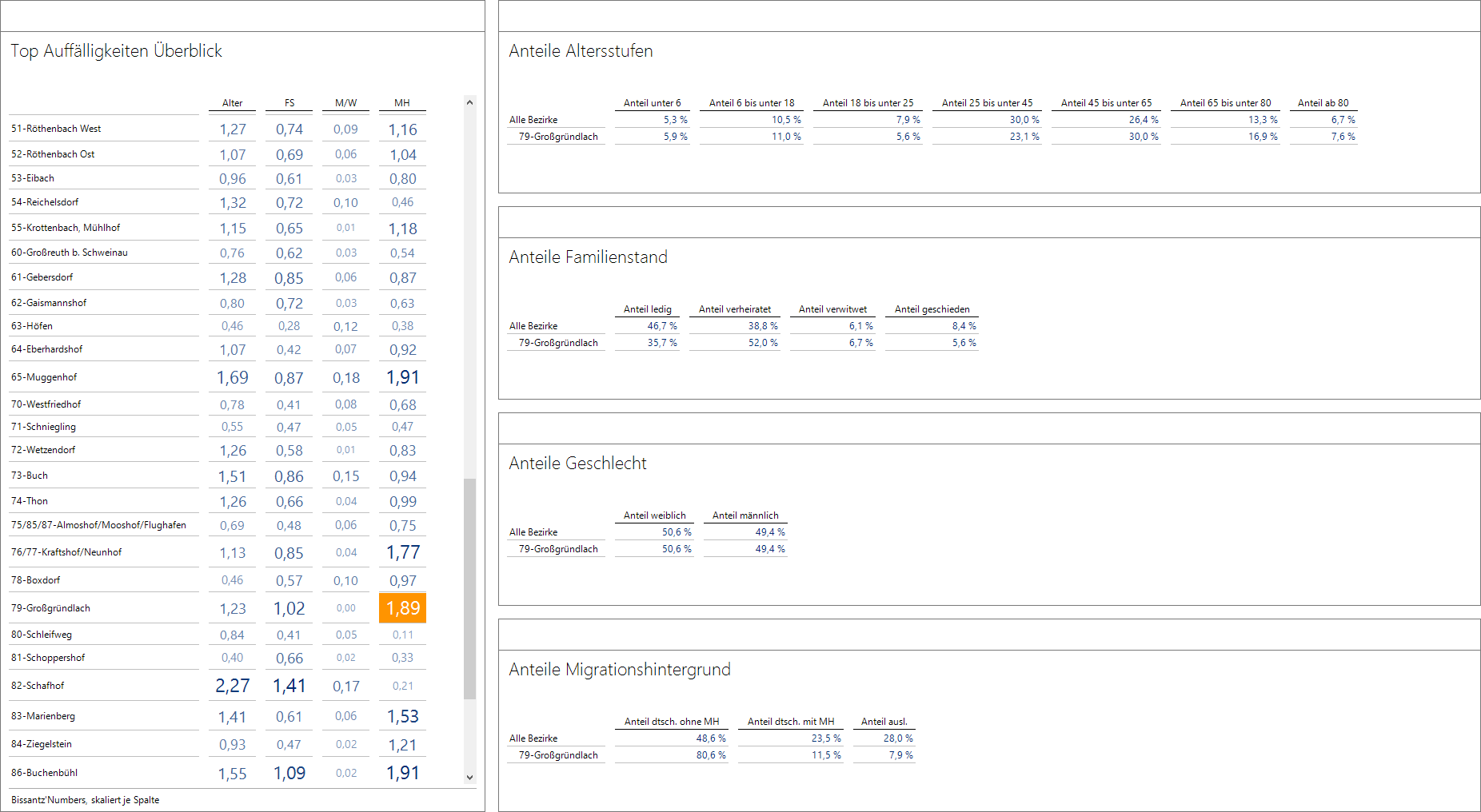
Man kann das noch beliebig weiterentwickeln. Zum Beispiel ließen sich diese aus dem Erwartungswert-Index berechneten Auffälligkeiten für alle vier Kategorien Alter, Familienbestand, Geschlecht und Migrationshintergrund ermitteln und in einem Multiples-Bericht darstellen. Über Strg + Mausklick auf eine der berechneten Auffälligkeiten wird der Bezirk auf die Berichte der rechten Hälfte übertragen und die jeweiligen Anteile angezeigt.
Auffälligkeiten im Bevölkerungsbestand
Da die in der bisherigen Manier definierten Auffälligkeiten bei den vier Kategorien durch die unterschiedliche Anzahl von Elementen unterschiedlich stark schwanken können, habe ich die Bissantz’Numbers spaltenweise skaliert.
Im Beispiel fällt der recht große Wert in 79-Großgründlach beim Migrationshintergrund auf und die Analyse der nun aktualisierten Tabelle rechts unten zeigt, dass hier im Gegensatz zu ganz Nürnberg der Anteil deutsch ohne MH sehr hoch liegt.
Mein Bezirk ist vollkommen unauffällig und war in keiner der Tabellen zu sehen.
Ich möchte noch einmal betonen, dass eine Analyse der multidimensionalen Daten noch bessere Ergebnisse erzielt hätte. Mit solchen Daten hätte man mit den Abhängigkeiten zwischen den Dimensionen zielgerichteter umgehen können. Beispielsweise würde man erkennen, dass aus einem hohen Anteil älterer Menschen ein höherer Frauenanteil und ein höherer Anteil verwitweter Personen folgt.
Genauso hätte man analysieren können, wer vor allem verheiratet ist (Kinder und Jugendliche sind es seltener).
Quellen
1. Daten von der Downloadseite nuernberg.bydata.de: Nürnberg: Bevölkerungsbestand, Merkmale zum Bevölkerungsbestand in Nürnberg nach zusammengefassten Statistischen Bezirken: Anzahl Einwohner nach Geschlecht, Familienstand, Altersgruppe, Migrationshintergrund, Datenbereitsteller: Amt für Stadtforschung und Statistik für Nürnberg und Fürth, Datenlizenz CC BY 4.0 (Creative Commons Namensnennung – 4.0 International); eigene Berechnungen (z. B. pro Fläche)
2. Shapefile der Bezirke für Nürnberg bei Openstreetmap.org: Nürnberg/Stadtteile. (2025, April 15). OpenStreetMap Wiki. Retrieved 08:46, April 29, 2025 from https://wiki.openstreetmap.org/w/index.php?title=N%C3%BCrnberg/Stadtteile&oldid=2837819.
3. Eingeblendeter Kartendienst von Terrestris aufbauend auf OpenStreetMap, Copyright OpenStreetMap contributors: Info zu Urheberrecht und Lizenz
4. Nenadic O, Greenacre M (2007). “Correspondence Analysis in R, with two- and three-dimensional graphics: The ca package.” Journal of Statistical Software, 20(3), 1-13. http://www.jstatsoft.org.
5. Mehr zu den Bezirken bei der Stadt Nürnberg: Nürnberg: Statistische Bezirke
6. Alle Angaben zu Zahlen und berechneten Werten ohne Gewähr.