Um in einer Menge mit vielen Elementen den Überblick behalten zu können, ist eine Zerlegung in eine überschaubare Anzahl von Segmenten notwendig. Oft liegen aber Label oder Kriterien, die über die Gruppenzugehörigkeit entscheiden, noch gar nicht vor – dann hilft die Clusteranalyse. Wenn sich Gruppen überlagern können, stellt die Zuweisung eines Elements zu genau einem Cluster nicht die optimale Lösung dar.
Werden in Lehrbüchern Beispiele für klassische Clusteranalysen benötigt, werden aus didaktischen Gründen gerne Daten verwendet, für die auch der ungeübte Anwender die Gruppen sofort erkennt. Seien beispielsweise pro Element der Menge zwei verschiedene Größen x und y gemessen worden. Die folgende Grafik zeigt im oberen Teil die erhaltenen Messwertpaare (x,y) und im unteren Teil die Cluster, die der K-Means-Algorithmus gefunden hat.
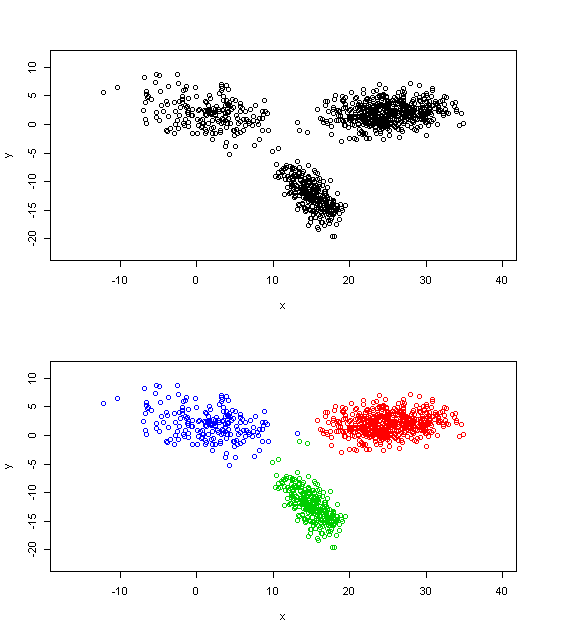
Clusterproblem mit relativ offensichtlichen drei Segmenten
Die gefundene Segmentierung wirkt angemessen. Über die Zuordnungen der Punkte im Niemandsland zwischen den Hauptwolken kann jedoch gestritten werden, wie beispielsweise im Falle der Dreiergruppe (1x Blau, 2x Grün), die möglicherweise auch der roten Gruppe hätte zugewiesen werden können.
Es gibt nun Clusteralgorithmen, die nicht die eindeutige Zuordnung eines Elements zu genau einem Segment verlangen, sondern die Zugehörigkeit durch Gewichte ausdrücken. Diese Gewichte addieren sich pro Element auf 1 auf. Wir stellen nun Gauß’sche Mischmodelle (auch bekannt als Gaussian mixture models) vor. Bei der Anwendung eines solchen Modells wird angenommen, dass die gegebenen Daten in einem zweistufigen Prozess generiert worden sind: Zunächst wird aus einer Menge von k mehrdimensionalen Normalverteilungen eine zufällig ausgewählt und dann wird mit dieser Normalverteilung eine Zufallszahl (bzw. ein Zufallsvektor) erzeugt.
Anpassen eines Modells bedeutet hier die Festlegung des Wahrscheinlichkeitsvektors, der die Auswahl der Normalverteilungen steuert und die simultane Festlegung der beteiligten Normalverteilungen durch Angabe der Erwartungswertvektoren und der Kovarianzmatrizen. Es wird somit direkt die Dichte der Beobachtungen modelliert. Zum Glück existiert der leistungsfähige Expectation-Maximization-Algorithmus (EM-Algorithmus), der die Optimierung der Parameter übernimmt.
Wird dieser Algorithmus beim gegebenen Datensatz eingesetzt, so ergibt sich der folgende Contourplot, der ausgewählte Höhenlinien der angepassten Dichte zeigt. Die Zahl gibt jeweils die Wahrscheinlichkeit an, mit der die zugehörige Normalverteilung ausgewählt wird:
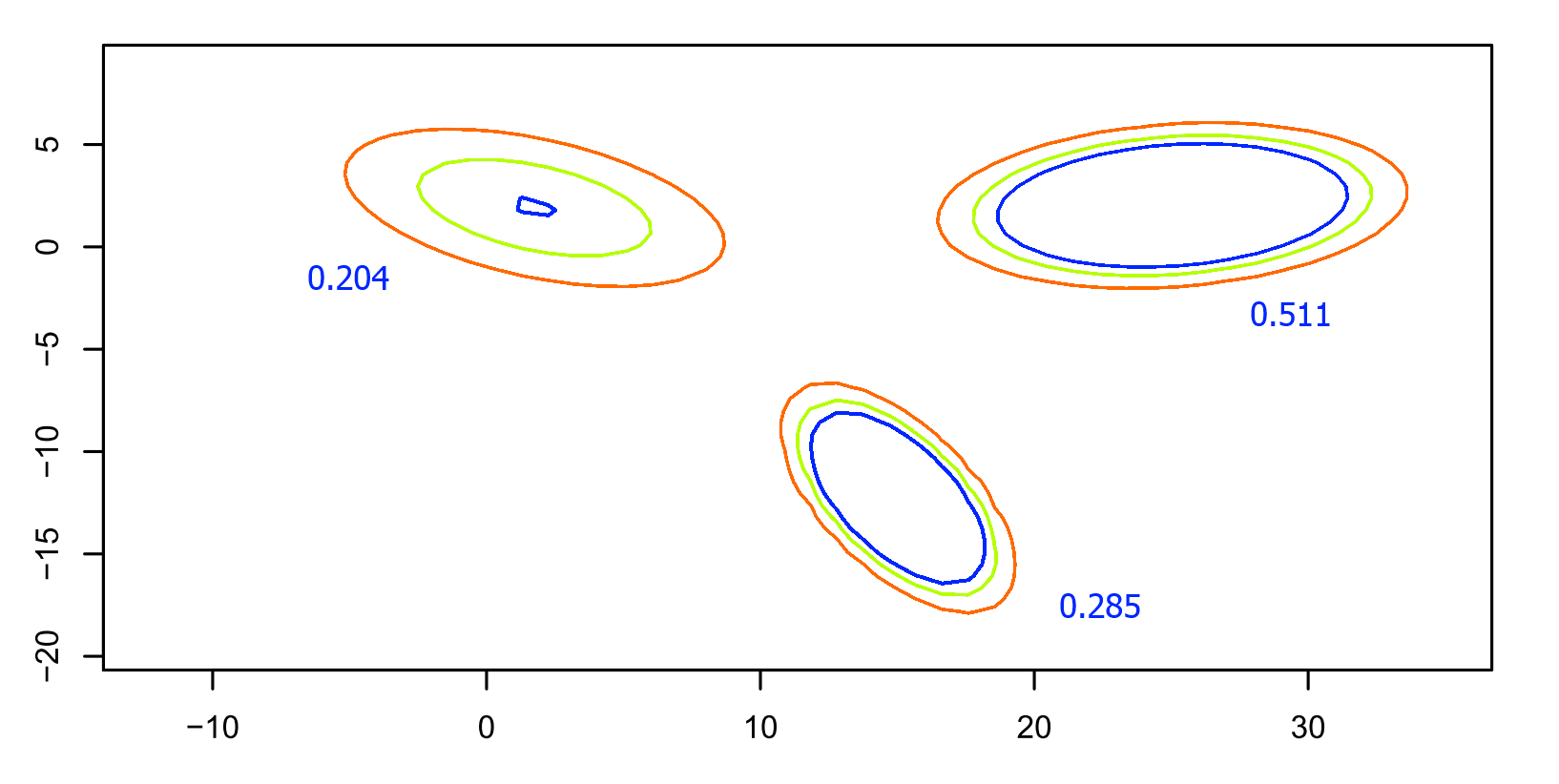
Wahrscheinlichkeiten und Höhenlinien (rot: 0.001, grün: 0.002, blau: 0.003) der angepassten Dichte
Die angezeigten Wahrscheinlichkeiten machen deutlich, dass der rechte Cluster ca. 50 Prozent der Beobachtungen stellt – eine Tatsache, die allein durch Betrachtung der Punktwolken nicht erkennbar ist. Die Dichte kann hier auch direkt in einer 3D-Darstellung gezeigt werden:
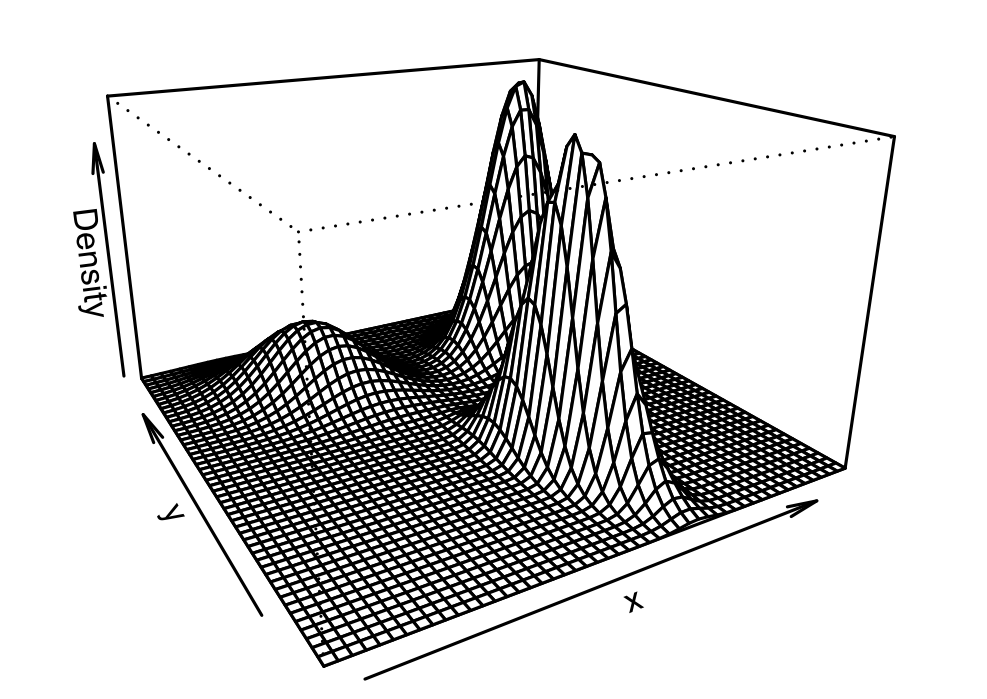
Darstellung der Dichte des Gauß’schen Mischmodells
Die beitragenden Normalverteilungen sind in diesem Fall noch deutlich erkennbar und überlappen sich eher in ihren Ausläufern. Es kann aber durchaus Konstellationen geben, bei denen sich die Normalverteilungen gegenseitig durchdringen.
Die Verwendung eines Misch-Modells bietet nun darüberhinaus die Möglichkeit, „Reverse Engineering“ zu betreiben. Für einen beliebigen Punkt (x,y) lässt sich über das angepasste Modell mittels der Anwendung des Bayes-Theorems die Wahrscheinlichkeit berechnen, dass eine ausgewählte der drei Normalverteilungen für die Generierung dieses Punktes verantwortlich gemacht werden kann. In der folgenden Grafik sind diejenigen Fälle schwarz eingefärbt, bei denen die maximale der drei Wahrscheinlichkeiten unterhalb von 90% bleibt. Bis auf diese fünf Punkte, zu denen auch die oben bereits erwähnte Dreiergruppe C, D und E gehört, können alle Beobachtungen relativ eindeutig einer Gruppe zugeordnet werden, die meisten (955 von 1000) sogar mit einer maximalen Wahrscheinlichkeit von mehr als 99.9%.
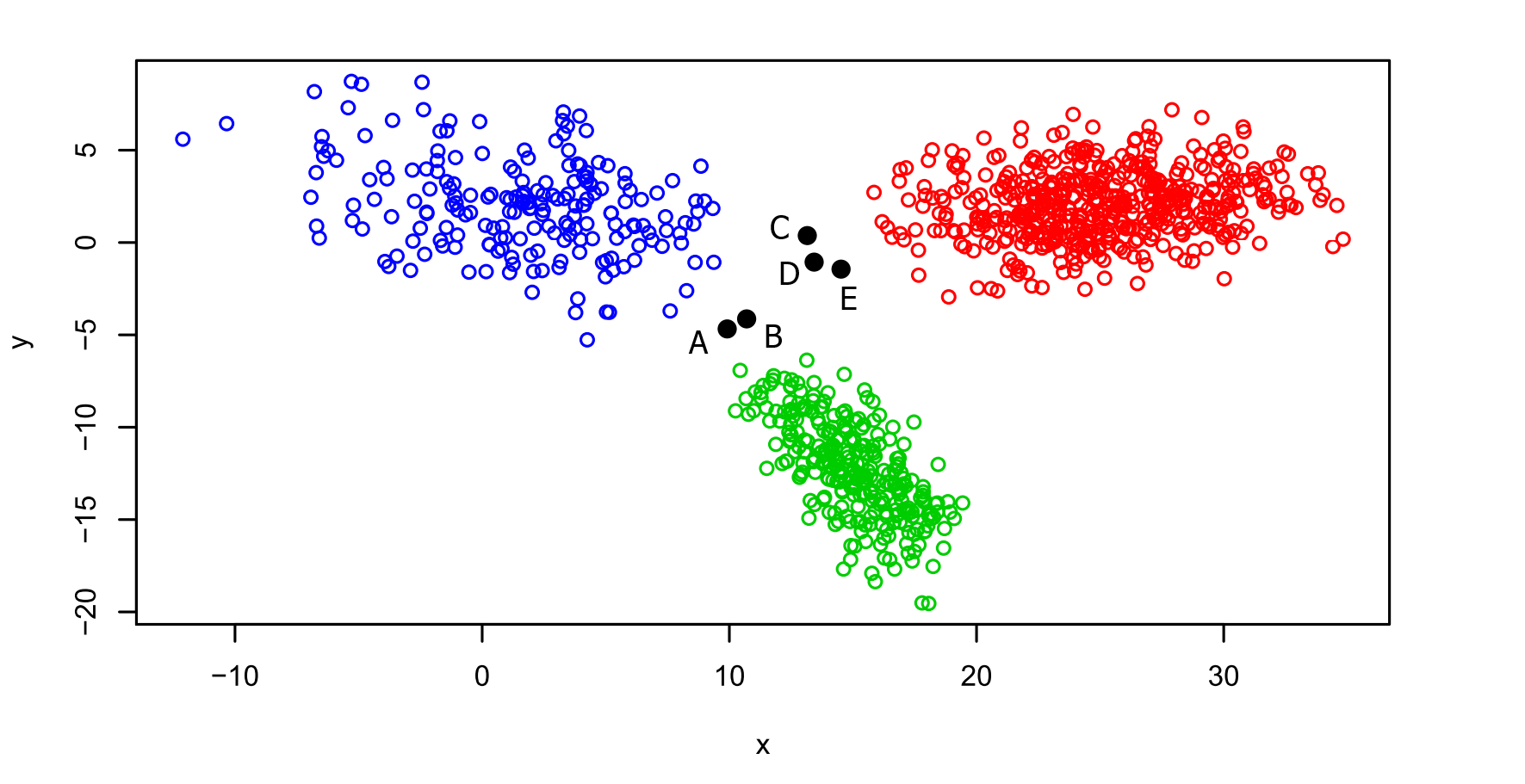
Unklare Fälle sind schwarz markiert.
Für diese fünf Punkte lauten die Wahrscheinlichkeiten der Gruppenzugehörigkeiten folgendermaßen:
| Punkt | Blau | Grün | Rot |
|---|---|---|---|
| A | 0.36 | 0.64 | 0.00 |
| B | 0.45 | 0.55 | 0.00 |
| C | 0.53 | 0.00 | 0.47 |
| D | 0.45 | 0.00 | 0.55 |
| E | 0.27 | 0.00 | 0.73 |
Wahrscheinlichkeiten für die Gruppenzugehörigkeiten
Wie auch schon die Grafik vermittelt, geht es bei den Punkten A und B um einen Zweikampf des blauen und des grünen Clusters und bei den Punkten C-E um die Entscheidung zwischen Blau und Rot; der K-Means-Algorithmus hatte diese drei Punkte noch zwischen Blau und Grün aufgeteilt.
Bei A und B neigt sich die Waage eher zu Grün, auch weil die zugehörige Wahrscheinlichkeit dieser Gruppe mit 0.285 größer ist als die 0.204 der blauen Gruppe. C wird eher der blauen, D und E eher der roten Gruppe zugerechnet. Die Entscheidungen bei B, C und D fallen knapp aus, wie die Wahrscheinlichkeiten nahe bei 0.5 vermitteln.
Die gegebenen Werte sind gut interpretierbar, wenn als sicher angenommen werden kann, dass eine der beteiligten Normalverteilungen für die Generierung zuständig war. Es könnte jedoch auch noch sein, dass Ausreißer vorliegen. Diese können an einem geringen Wert der Dichten aller beteiligten Normalverteilungen erkannt werden.
