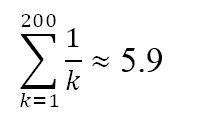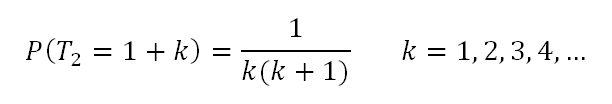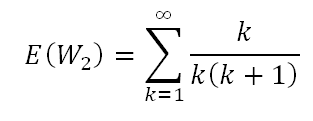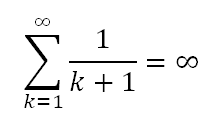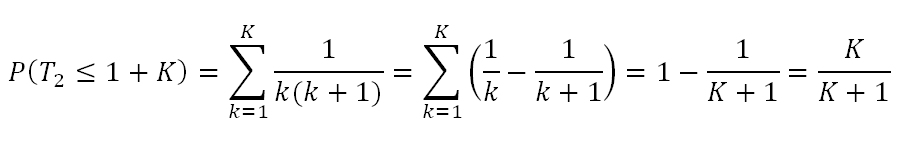Schneller, höher, weiter – in einer Zeit des stetigen Wachstums werden ständig neue Rekorde erwartet. Ein Gewinn einer AG, der nicht der prognostizierten Erwartung entspricht, auch wenn er deutlich über dem Vorjahreswert liegen sollte, wird von einer Gewinnwarnung begleitet. Wir widmen uns heute der Frage, welche Verbesserungen im Vergleich zu vorangegangenen Werten eigentlich erwartet werden können, wenn Stagnation vorherrscht.
Unter Stagnation verstehen wir hier nicht zwingend, dass eine Kennzahl jede Periode immer den gleichen Wert aufweisen muss, sondern wir nehmen an, dass durchaus zufällige Schwankungen um einen konstanten Wert auftreten können. Wir gehen weiterhin von einer sehr feinen Skala aus, sodass sich Werte niemals exakt wiederholen. Geeignet ist die Annahme einer stetigen Verteilung, die sich im Zeitverlauf von Periode zu Periode nicht ändert.
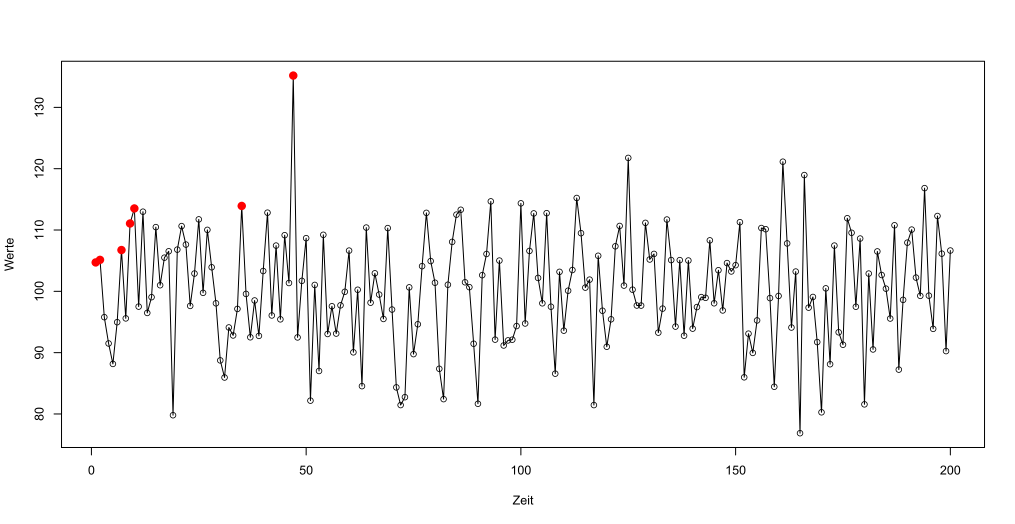
Rote Markierungen: Eine neue Bestmarke wurde erzielt
Wir behandeln hier den prospektiven Fall, befinden uns also im Zeitpunkt t=0 und haben noch keine Werte beobachtet. Folgende Fragestellungen drängen sich typischerweise auf: Mit welcher Wahrscheinlichkeit liefert der zu einem bestimmten Zeitpunkt t beobachtete Wert ein neues Maximum? Wie lange muss man im Durchschnitt warten, bis zum dritten Male ein Höchststand beobachtet wurde? Wie viele Höchststände habe ich typischerweise nach 200 Perioden gesehen?
Wir versuchen nun, einige dieser Fragen zu beantworten.
Nehmen wir einmal an, dass eine Kennzahl jede Periode aus einer Normalverteilung mit Erwartung 100 und Standardabweichung 10 generiert wird. Die oben dargestellte Zeitreihe stellt einen möglichen Verlauf von vielen dar. Es sind diejenigen Perioden markiert, die einen jeweiligen neuen Höchststand im bisherigen Zeitverlauf ergeben (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!).
Während anfangs die Rekorde nur so purzeln, verlängern sich im Zeitverlauf die Dürreperioden, bis ein neuer Rekordwert auftritt. Das zum Zeitpunkt t=47 beobachtete Maximum wird in den nächsten 153 Perioden nicht mehr übertroffen.
Wie wahrscheinlich ist es, in der n-ten Periode ein neues Maximum zu erhalten?
Wir befinden uns im Zeitpunkt t=0 und haben noch keine Werte beobachtet. Bei n erzeugten Werten X(1), X(2), …, X(n) besitzt jeder einzelne die gleiche Wahrscheinlichkeit, das Maximum darzustellen, nämlich 1/n. Das gilt natürlich auch für den letzten Wert X(n). In der Vorausschau werden wir deshalb mit einer Wahrscheinlichkeit 1/t zum Zeitpunkt t ein neues Maximum beobachten. Dieser Zusammenhang ist universell richtig und hängt auch nicht von der genauen Gestalt der stetigen Verteilung ab.
Hieraus lässt sich auch einfach die erwartete Anzahl von Höchstständen während der 200 Perioden berechnen. Diese entspricht der Partialsumme
In unserer simulierten Zeitreihe waren es sieben Maxima. Man könnte mit dieser Formel auch ermitteln, nach welchem Zeitraum zehn beobachtete Höchststände erwartet werden können; dies ist erst nach überraschend hohen 12367 Perioden der Fall. Die folgende Tabelle gibt an, wie viele Perioden vorliegen müssen, um eine vorgegebene erwartete Anzahl von Höchstständen zu erreichen oder zu übertreffen:
| Anzahl Maxima | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Anzahl Perioden | 1 | 4 | 11 | 31 | 83 | 227 | 616 | 1674 | 4550 | 12367 | 33617 | 91380 |
Die Zeitabstände wachsen rasant an, um jeweils ein weiteres Maximum erwarten zu können. Trotzdem kann zu jeder vorgegebenen, noch so großen Anzahl von Maxima ein passender Zeitpunkt gefunden werden, bloß strebt dieser bereits für moderate Vorgaben mit Riesenschritten in die ferne Zukunft.
Reisen wir wieder in der Zeit zurück nach t=0 und stellen die Frage, wie lange wir im Durchschnitt warten müssen, bis der in t=1 beobachtete Wert zum ersten Mal übertroffen wird. Da der zu t=1 beobachtete Wert das erste Maximum darstellt, suchen wir somit die anschließende Wartezeit bis zum zweiten Maximum.
Es lässt sich zeigen, dass die Wahrscheinlichkeit, weitere k Perioden bis zum zweiten Maximum warten zu müssen,
beträgt. In einer Simulation haben wir einmal 100.000 Folgen analog zu unserem Beispiel erzeugt und jeweils festgehalten, wie lange die Wartezeit bis zum zweiten Maximum betrug und dann die Anteile der Durchläufe bestimmt, die jeweils eine Wartezeit k besaßen. Wurde in den nächsten 100 Perioden der erste Wert zu t=1 noch nicht übertroffen, wurde der Simulationslauf abgebrochen und dem Wert 101, der hier als Sammelcontainer dient, zugewiesen. Die folgende Abbildung vergleicht Theorie (rote Linie) und Simulationswerte (schwarze Kreise):
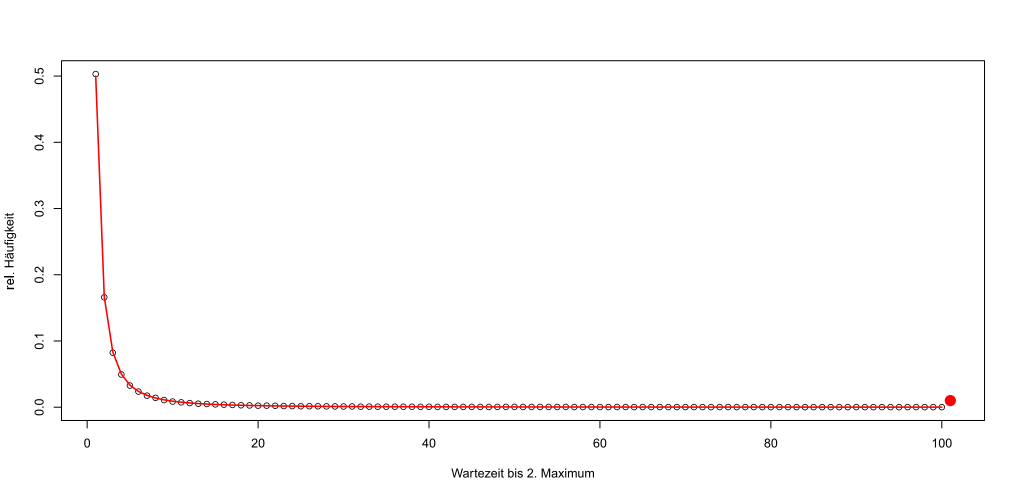
Anteil der Durchläufe für bestimmte Wartezeiten bis zum zweiten Maximum
Eine Darstellung mit den Logarithmen der Anteile ist leichter zu erfassen:
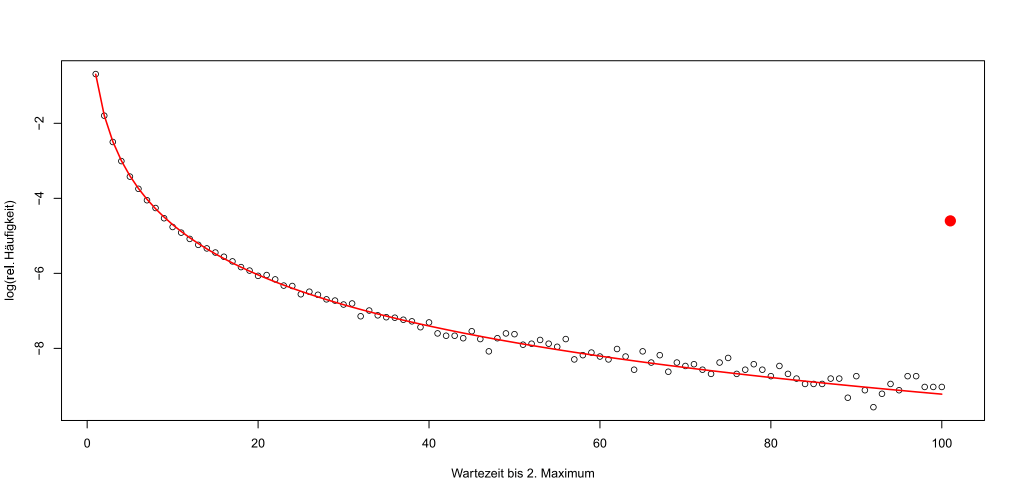
log(Anteil) der Durchläufe nach Wartezeit
Theorie und Simulation passen somit gut zusammen. Wie sieht es nun aus mit der erwarteten Wartezeit bis zum 2. Maximum? Diese lässt sich berechnen zu
Das k lässt sich herauskürzen und wir erhalten einen Ausdruck
der identisch zur harmonischen Reihe ab dem zweiten Summanden ist und deshalb nicht konvergiert. Die erwartete Wartezeit bis zum zweiten Maximum ist also verblüffenderweise unendlich groß, obwohl wir korrekt berechnet hatten, dass nach vier Perioden im Mittel zwei Maxima beobachtet worden sind. Sollten wir somit bei Stagnation froh sein, überhaupt ein Übertreffen des ersten Wertes erleben zu dürfen?
Betrachten wir einmal die Wahrscheinlichkeit, maximal K weitere Perioden warten zu müssen. Diese lässt sich zu einem recht einfachen Ausdruck umformen:
Mit Wahrscheinlichkeit 3/4 beobachten wir das zweite Maximum bis zum Zeitpunkt t=4 und mit Wahrscheinlichkeit 100/101~0.990099 sehen wir das zweite Maximum innerhalb der nächsten 100 Perioden.
Die bisherigen Ergebnisse lassen sich folgendermaßen zusammenfassen: Zum Zeitpunkt t=4 ist die erwartete Anzahl der beobachteten Maxima ungefähr 2 (der exakte Wert ist 1+1/2+1/3+1/4=25/12), zum Zeitpunkt t=4 ist auch mit Wahrscheinlichkeit 3/4 das zweite Maximum bereits beobachtet worden, aber trotzdem ist die erwartete Wartezeit bis zum zweiten Maximum unendlich groß.
Wächst der Beobachtungshorizont K, so strebt die Wahrscheinlichkeit, das zweite Maximum tatsächlich zu beobachten, zwar gegen 1, aber mit einer nicht zu vernachlässigenden Restwahrscheinlichkeit können beliebig hohe Wartezeiten auftreten, die dafür sorgen, dass die erwartete Wartezeit nicht endlich ist. Der Wert zum Zeitpunkt t=47 in unserer Beispielzeitreihe lässt erahnen, dass durch extreme Ausreißer neue Maxima für lange Zeit Mangelware bleiben.
Für die Wartezeiten bis zum dritten, vierten,…, m-ten Maximum ändert sich qualitativ nichts, die erwarteten Wartezeiten sind ebenfalls unendlich groß, aber die Wahrscheinlichkeiten, die weiteren Maxima innerhalb eines festen Horizonts K ab dem vorhergehenden Maximum zu erleben, sinken mit dem Wert m. Es lässt sich sogar zeigen, dass für die Gesamtwartezeit bis zum m-ten Maximum für große m hauptsächlich die Wartezeit zwischen dem m-1-ten Maximum und dem m-ten Maximum verantwortlich ist.
Die genannten theoretischen Ergebnisse über Wartezeiten und Wahrscheinlichkeiten, die bereits zum Zeitpunkt t=0 formuliert werden können, sind deshalb so faszinierend, da sie überhaupt nicht von der Verteilung der Kennzahl abhängen, solange diese stetig ist.
Interessant ist es auch, bei unbekannter Verteilung auf der Basis der bisher beobachteten Werte Aussagen über die Möglichkeiten zukünftiger, noch extremerer Werte abzuleiten. Aber dies ist ein anderes Thema, dem wir uns in einem separaten Blogbeitrag widmen sollten.