Sehr häufig trifft der Anwender auf Dimensionsebenen, bei denen die Annahme plausibel ist, dass alle Elemente der Ebene in der Faktentabelle ungefähr gleich häufig auftreten sollten. Jedoch ist nicht zwingend davon auszugehen, exakt gleiche Häufigkeiten anzutreffen. Wann sind Abweichungen von der Erwartung so groß, dass sie ernst genommen werden müssen?

Wird ein fairer Würfel 600-mal geworfen, so beträgt die erwartete Anzahl jeder der sechs Augenzahlen 100. Das bedeutet aber nicht, dass nun zwingend genau diese Konstellation gleicher Häufigkeiten eintritt; der Fall, dass jede Augenzahl exakt 100-mal vorkommt, ist mit einer Wahrscheinlichkeit von ungefähr 0.000000246 eher sehr selten. Die folgende Tabelle zeigt die erhaltenen Augenzahlen, falls dieses Experiment mit einem fairen Würfel 20-mal wiederholt wird. Von 75 Fünfen bis 122 Dreien werden durchaus beachtliche Abweichungen beobachtet (für eine vergrößerte Darstellung bitte auf die Grafik klicken!).

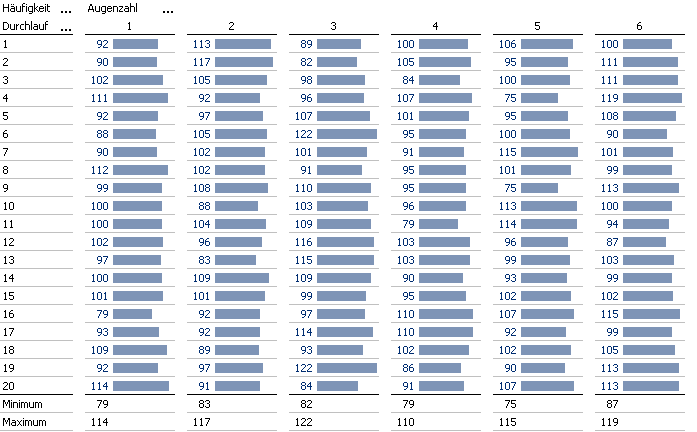
Natürliche Schwankungen der Anzahlen bei einem fairen Würfel

Ist nun ein Ergebnis mit den Häufigkeiten 81-84-117-92-105-121 besonders auffällig oder nicht? Was passiert, wenn ich ein solches Ergebnis mit dem Resultat 208-167-164-158-163-140 vergleichen möchte, das entstanden ist, als ein anderer Würfel 1000-mal geworfen wurde? Wie sieht es mit der Verteilung aller jemals gezogenen Lottozahlen (also 49 Häufigkeiten bis zum Stichtag 18.1.2014) oder der später eingeführten Superzahl (eine einstellige zusätzlich gezogene Ziffer) aus? Um die Brücke zu betriebswirtschaftlich relevanten Zahlen zu schlagen, folgen mögliche Beispiele aus der Praxis:

• Die Bestellhäufigkeiten der drei Farbvarianten Silber, Weiß und Rot eines Automobils betrugen bisher 117-84-312. Diese Ungleichverteilung geht gefühlt über Zufälligkeit hinaus, aber wie weit?
• Ein Produkt wurde im letzten Monat in vier Filialen, die im letzten Jahr vergleichbare Umsätze erzielt hatten, mit den folgenden Häufigkeiten verkauft: 245-315-180-200. Hinreichender Grund, die Filialleiter der Märkte anzusprechen?
• Das neue Tablet wurde am ersten Tag von 1571 Männern und 983 Frauen gekauft. Hat der Begriff Fanboy doch seine Berechtigung?

Hier sind auch Beispiele vertreten, bei denen wir ahnen, dass die Dimensionselemente nicht gleichwahrscheinlich sind. Um aber den Grad der Ungleichverteilung messen zu können, übernehmen wir die Rolle des Advocatus Diaboli, der von der Hypothese der Gleichheit ausgeht, um dann umso wirkungsvoller etwaige Abweichungen messen und verkünden zu können.

Wir hatten bereits in Den Zufall zu Fall bringen Dimensionen nach ihrem Einfluss auf Erfolgsquoten bewertet und sortiert. Ein ähnlicher Ansatz führt zu einem Score, der Abweichungen von der Hypothese, dass alle Dimensionselemente gleichwahrscheinlich sind, beziffert und für eine Sortierung nach Relevanz verwendet werden kann. Die Herausforderung bestand darin, Fälle mit unterschiedlichen Stichprobengrößen und unterschiedlicher Anzahl von Dimensionselementen vergleichbar zu machen. Wie im zitierten Blogartikel kommt es auch hier zu Schwierigkeiten, große Abweichungen verlässlich zu bewerten. Unser Score löst die auftretenden Probleme und bewertet die Szenarios folgendermaßen:

Die Scores der Szenarios

Scores mit einem Wert<1 sind unauffällig, ab einem Wert von 2 sind die Auffälligkeiten schon größer. Wir sehen zum Glück, dass gegen die Annahme gleichwahrscheinlicher Lotto- bzw. Superzahlen nichts einzuwenden ist. Die Würfel sind leicht verdächtig, und schließlich können bei den betriebswirtschaftlichen Szenarios markante Auffälligkeiten gefunden werden. An der Spitze stehen die Farbvarianten des Automobils und die Tabletverkäufe nach Geschlecht. Diese beiden Fälle stellten auch die Herausforderung dar, da bei ihnen der Score auf normalem Wege wegen beschränkter Rechengenauigkeit vorliegender Algorithmen nicht wie gewünscht ermittelt werden konnte und verlässliche Approximationen hergeleitet werden mussten.

Bei den Fällen, bei denen ein hoher Score darauf hinweist, dass eher nicht davon auszugehen ist, dass eine gleichmäßige Verteilung der Häufigkeiten auf die Dimensionselemente vorliegt, ändert sich unter Umständen das Verständnis, was wohl unter „normal“ zu verstehen ist. Der Automobilhersteller kann beispielsweise seine Erwartungen an die Beliebtheit der Farben anpassen, indem er von nun an Plananteile verwendet, die den bisher beobachteten Anteilen entsprechen.