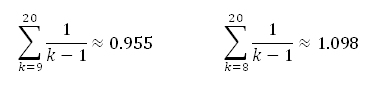Nehmen wir einmal an, dass Sie damit beauftragt worden sind, aus einer Menge von Bewerbern den besten auszusuchen. Es gibt nur einen Haken: Die Bewerber stellen sich der Reihe nach vor und Sie müssen sich sofort entscheiden, haben somit nicht die Möglichkeit, auf einen bereits abgelehnten Kandidaten zurückzugreifen. Welche Strategie ist optimal, um tatsächlich den besten Kandidaten einzustellen?
Dieses Problem taucht seit den 60ern in verschiedenen Varianten auf; in der bekanntesten Variante geht es um den Posten eines Sekretärs bzw. einer Sekretärin, den es zu besetzen gilt; manchmal sind es auch für die Heirat infrage kommende Partner, die sich verständlicherweise nach einem bereits gegebenen Korb wohl so gut wie nie umstimmen lassen. Es könnte auch sein, dass Sie ein Automobil annonciert haben, das Sie zum Höchstpreis verkaufen möchten und sich nun voneinander unabhängige Angebote nennen lassen, bis Sie endlich eines akzeptieren. Als Einstieg in die Thematik empfiehlt sich der Artikel „Who Solved the Secretary Problem?“ von Thomas S. Ferguson, der 1989 auf Spurensuche gegangen ist (*).
Um die nun beschriebene Variante genauer abzugrenzen, seien einige zu erfüllende Kriterien genannt:
- Es gilt mit Oscar Wilde: „Ich habe einen ganz einfachen Geschmack: Ich bin immer mit dem Besten zufrieden“. Wenn Sie auch bereits nur den zweitbesten Kandidaten einstellen, ist Ihre Mission gescheitert.
- Die Reihenfolge der Kandidaten ist zufällig.
- Keine zwei Kandidaten haben exakt gleiche Eignungen.
- Die Anzahl der Kandidaten ist bekannt.
In Analogie mit dem Bewerberbeispiel wollen Sie beim Autoverkauf somit nicht einen angemessenen Preis erzielen, sondern den maximal möglichen.
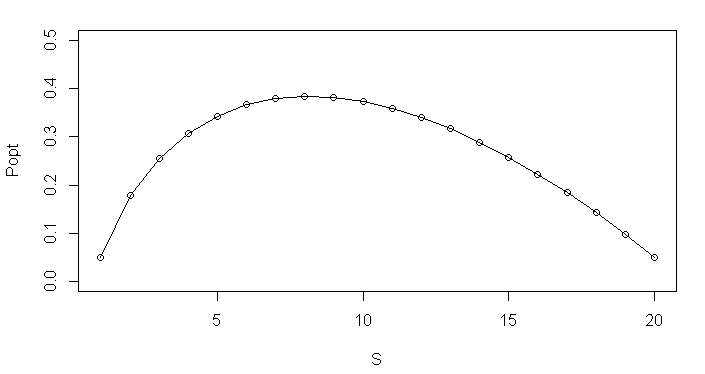
Wahrscheinlichkeit in Abhängigkeit von S, tatsächlich den optimalen Kandidaten zu wählen
Es kann nun gezeigt werden, dass die optimale Regel von der Form sein muss, die ersten S-1 Kandidaten einfach zu ignorieren und ab dem S-ten Kandidaten denjenigen zu nehmen, der als erster besser ist als alle bisher beobachteten. Die Grafik zeigt bei 20 Kandidaten die von S abhängige Wahrscheinlichkeit, tatsächlich den besten zu erwischen.
Nehmen Sie bereits den ersten Kandidaten (S=1), so ist dieser nur mit Wahrscheinlichkeit 1/20 der beste. Warten Sie bis zum Schluss (S=20), so ist dieser ebenfalls nur mit Wahrscheinlichkeit 1/20 der beste. Es geht aber besser:
In diesem Beispiel ist das optimale S=8 und die Wahrscheinlichkeit, den besten Kandidaten zu erwischen (der dann prinzipiell an jeder Position von 8 bis 20 liegen kann), beträgt dann ca. 38.4%. Welche Szenarios gibt es?
- Sie haben tatsächlich den besten Kandidaten gefunden. Glückwunsch!
- Sie finden ab dem S-ten Kandidaten zwar einen, der besser ist als alle bisherigen, aber es ist nicht der beste, da dieser eigentlich noch kommt. Zu früh zugegriffen, leider Pech gehabt!
- Der beste Kandidat war schon unter den ersten S-1. Sie wählen somit überhaupt keinen Kandidaten aus, da Sie die Eignung des besten nicht mehr übertreffen können.
Die folgende Grafik zeigt den schönen Fall, bei dem die Strategie zum Erfolg geführt hat (Bemerkung: Zu jedem Zeitpunkt außer t=20 sind nur die relativen Anordnungen der bisher gesehenen Kandidaten bekannt, nicht ihre absoluten Positionen innerhalb aller Kandidaten).
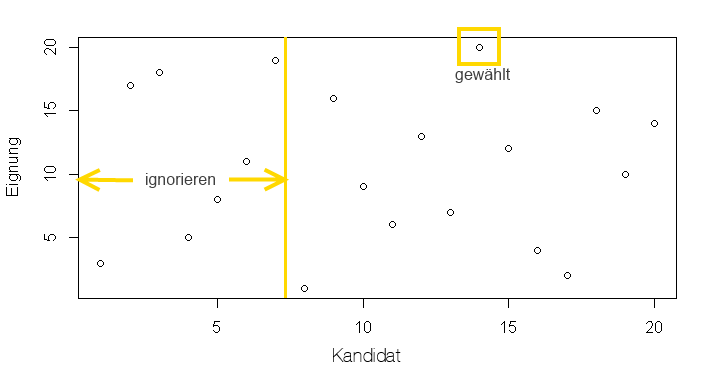
Die ersten sieben Kandidaten abwimmeln, ab dem achten auf der Lauer liegen, bei Kandidat 14 zuschlagen: Treffer versenkt!
F. Thomas Bruss hat in seinem Artikel „Sum the Odds to One and Stop“ (**) bereits in der Überschrift die richtige Strategie genannt: Um das optimale S zu bestimmen, müssen rückwärts von hinten (k=20, 19, 18,…) die Kehrwerte 1/(k-1) aufsummiert werden, bis in der Summe 1 erreicht oder überschritten wird.
Da
gilt, ist somit das optimale S=8.
Bei einer sehr großen Anzahl n von Kandidaten lässt sich zeigen, dass S ungefähr n/e (e=Eulersche Zahl 2.718282…), also ca. 0.368*n ist. Auch die Wahrscheinlichkeit, den global besten Kandidaten zu erwischen, beträgt mit 1/e ungefähr 36.8%. Dies stellt eine nicht zu unterschreitende untere Grenze dar. Selbst bei 1.000.000 Bewerbern werden Sie erstaunlicherweise mit dieser Strategie mit 36.8% Wahrscheinlichkeit den besten auswählen, wobei Sie die ersten ca. 368.000 zwar begutachten und sich den besten merken, aber ansonsten alle gleich durchwinken.
Als einfach zu merkende Daumenregel gilt, dass bei der optimalen Regel ungefähr die ersten 40% der Bewerber begutachtet, aber ignoriert werden und dann der erste Bewerber (falls es ihn gibt) genommen wird, der besser ist als alle bisher beobachteten.
Sollten Sie jedoch zu den Bewerbern gehören und eine Einladung zu einem sehr frühen Termin erhalten haben, vergrößern Sie somit ihre Chancen bei einem mathematisch bewanderten Personalchef, wenn Sie verspätet eintreffen (Empfehlung ohne Gewähr!).
Übrigens hat Robert J. Vanderbei (***) den Fall untersucht, lieber den zweitbesten Kandidaten zu finden, da bei diesem wohl weniger Starallüren anzunehmen seien. Vanderbei hat herausgefunden, dass es schwieriger ist, den zweitbesten Kandidaten auszuwählen, da hier die garantierte Wahrscheinlichkeit nur 25% beträgt. Hier wird bei der optimalen Strategie gleich die komplette erste Hälfte der Bewerber ignoriert und dann der erste Bewerber genommen, der unter den bisherigen Kandidaten der zweitbeste ist.
Es gibt wie bereits erwähnt sehr viele Varianten des Problems, z.B. mit Zielen wie etwa der Maximierung der erwarteten Eignung des gewählten Kandidaten oder des erwarteten Ertrags, mit und ohne Berücksichtigung von zeitabhängigen Kosten. Es hat sich ein ganzer Wissenschaftszweig entwickelt, der sich mit Problemen dieser Art beschäftigt.
(*) Thomas. S. Ferguson, Who Solved the Secretary Problem?, Statistical Science, Vol.4, No. 3 (Aug. 1989), pp. 282-289.
(**) F. Thomas Bruss, Sum the Odds to One and Stop, The Annals of Probability, Vol. 28, No. 3 (2000), pp. 1384-91.
(***) Robert J. Vanderbei, The Postdoc Variant of the Secretary Problem, PDF unter http://www.princeton.edu/~rvdb/tex/PostdocProblem/PostdocProb.pdf (letzter Zugriff 17.3.2014)