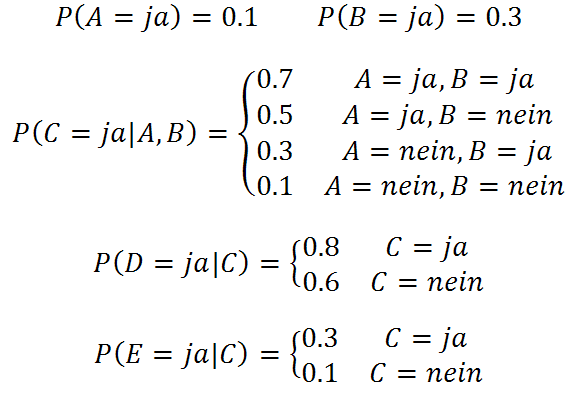Abhängigkeiten, die zwischen zufälligen Größen existieren, können häufig in einem Graphen einprägsam wiedergegeben werden. Wir erläutern heute Ansätze, die es auf relativ einfache Weise ermöglichen, Aussagen über nicht beobachtete Variablen abzuleiten.

In unserem Beispiel nehmen wir an, dass ein Unternehmen sowohl auf seiner Internetpräsenz, als auch im TV für ein neues Waschmittel wirbt. Ein zufällig in einer Straßenumfrage angesprochener Kunde kennt das Produkt – möglicherweise verursacht durch die Werbung – bereits bewusst oder eben nicht. Er wird gefragt, ob er eine kleine Probe gratis haben möchte und ob er seine Email-Adresse zwecks Zusendung eines Newsletters mit weiteren Produkten hinterlassen möchte. Insgesamt gibt es fünf Variablen mit den folgenden Bedeutungen:

1. A: Person hat das Produkt auf der Webseite bereits gesehen (ja/nein)
2. B: Person hat das Produkt in der TV-Werbung gesehen (ja/nein)
3. C: Person kann sich bewusst an das Produkt erinnern (ja/nein)
4. D: Person möchte die Gratisprobe (ja/nein)
5. E: Person möchte die Email-Adresse hinterlassen (ja/nein)

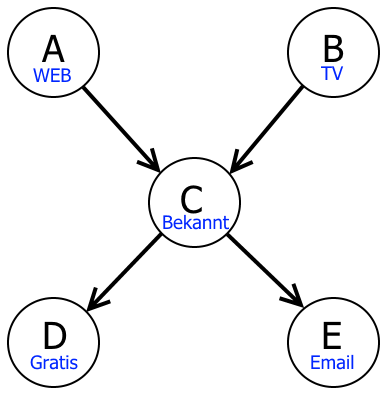
Der folgende Graph zeigt qualitativ, welche Einflüsse zwischen den Größen angenommen werden:

Graph der Abhängigkeiten

Was besagt dieser Graph? Hier wird beispielsweise angenommen, dass der Konsum von Fernsehwerbung unabhängig vom Besuch der Webseite ist. Man könnte auch argumentieren, dass eine positive Korrelation vorliegen könnte: Personen, die Fernsehen schauen, sind mit höherer Wahrscheinlichkeit auch im Web unterwegs. Auch halbwegs plausibel klingt die entgegengesetzte Annahme, dass die Zeit vor dem Fernseher auf Kosten der Zeit im Web geht. Wir bleiben bei der Annahme der Unabhängigkeit.

Dass nur von C aus Pfeile auf D und E zeigen und nicht direkt von A oder B, bedeutet, dass die Entscheidung für eine Gratisprobe oder den Newsletter nur von der Tatsache abhängt, ob das Waschmittel bereits bekannt war oder nicht, es aber keine Rolle mehr spielt, ob das Produkt im Web und/oder im TV gesehen wurde.

Hat man sich auf eine plausible Struktur der Abhängigkeiten festgelegt, gilt es, die Darstellung quantitativ zu füllen. Möchte man ein solches sogenanntes Bayes’sches Netzwerk herleiten, lässt sich die Tatsache ausnutzen, dass die gemeinsame Wahrscheinlichkeitsfunktion aller 5 Variablen hier eine spezielle Struktur annimmt:

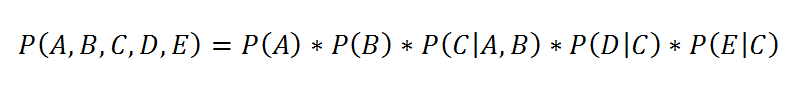
Gemeinsame Wahrscheinlichkeitsfunktion

Beim Vergleich mit der Netzstruktur wird die starke Korrespondenz zur Formel deutlich. Jeder Knoten ohne Vorgänger steht in der Formel als einfache Wahrscheinlichkeit da, hier also P(A) und P(B).
Jeder andere Knoten mit Vorgängern ist ebenfalls vertreten, diesmal als bedingte Wahrscheinlichkeit P(Knoten|Vorgänger). Die hinteren drei Faktoren fallen unter diese Rubrik.

Diese fünf Wahrscheinlichkeitsfunktionen müssen nun bestimmt werden, sei es durch Schätzung, durch Annahmen oder durch Experimente. Letztendlich gelange man beispielsweise zu den folgenden Wahrscheinlichkeitsfunktionen:

Wahrscheinlichkeitsfunktionen

Die Wahrscheinlichkeiten für die Nein-Fälle ergeben sich jeweils als Differenz zu 1, beispielsweise ist P(C = nein | A = ja, B = ja) = 1-0.7 = 0.3.

Nun sind wir soweit, das vollständig definierte Bayes’sche Netz für Schlussfolgerungen nutzen können. Beispielsweise können wir fragen, wie groß die Wahrscheinlichkeit ist, dass eine Person, von der wir nur wissen, dass sie die Werbung im Fernsehen gesehen hat, bei Ansprache auf der Straße den Newsletter bestellen wird. Hier handelt es sich also um eine Voraussage:

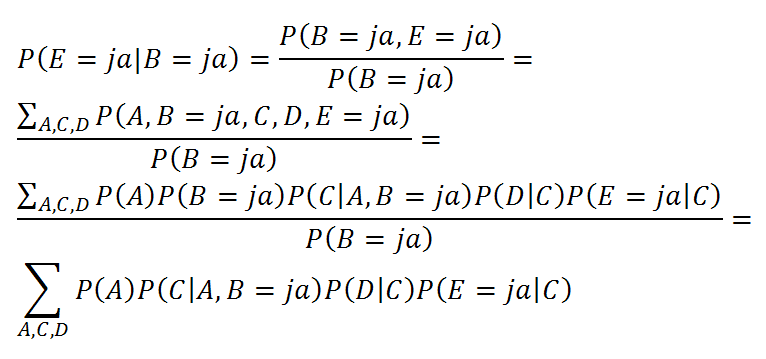
Ableitung der Wahrscheinlichkeit einer Newsletter-Bestellung, gegeben “TV-Werbung gesehen”

In der Summation müssen insgesamt 8 mögliche Kombinationen von A, C und D durchgespielt werden. Hier bei diesem übersichtlichen Beispiel ist das noch ohne Probleme durchführbar, bei sehr großen Netzen kann es passieren, dass man sich mit approximativen Verfahren begnügen muss. Hier ergibt sich nach etwas Rechnerei, dass P(E = ja | B = ja) = 0.168 beträgt.

Aber Schlussfolgerungen können auch rückwärts laufen und nach der Ursache von Beobachtungen fragen. Sei beispielsweise nach der Wahrscheinlichkeit gefragt, dass jemand die Werbung im TV gesehen hat, wenn die Person behauptet, das Produkt bewusst zu kennen. Gesucht ist somit

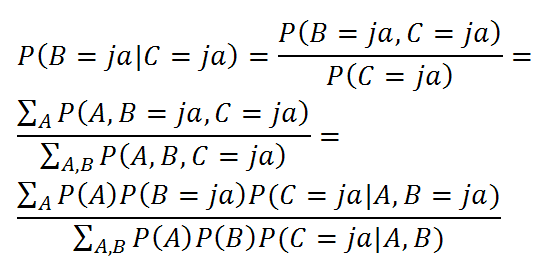
Ableitung der Wahrscheinlichkeit, die Werbung gesehen zu haben, gegeben “Das Produkt ist mir bekannt”

Hier ergibt sich P(B = ja | C = ja) = 0.51. Wie ändert sich die Berechnung, wenn der angesprochene Passant nebenbei bemerkt, das Produkt bereits auf der Homepage gesehen zu haben? Wir suchen somit

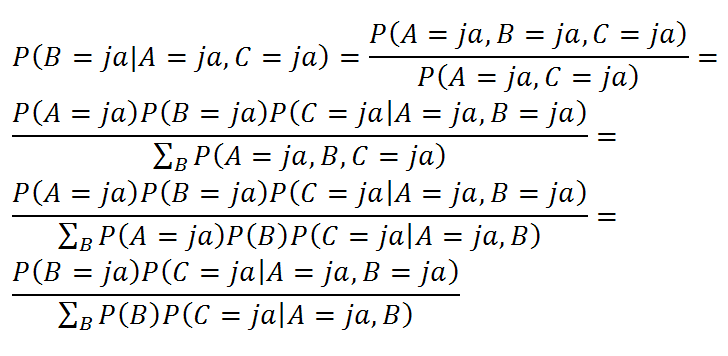
Ableitung der Wahrscheinlichkeit, die Werbung gesehen zu haben, gegeben “Das Produkt ist mir bekannt und ich habe es auf der Homepage gesehen”

Nun ergibt sich P(B = ja | A = ja, C = ja) = 0.375 < 0.51. Dieses Phänomen, dass bei gegebenem Effekt (“kenne das Produkt”) die Wahrscheinlichkeit einer Ursache (“im TV gesehen”) sinkt, wenn eine andere Ursache (“im Web gesehen”) bekannt ist, nennt man Wegerklären (im Engl. “explaining away”).

Ist eine Teilmenge der 5 Variablen mit den Werten gegeben, lassen sich, so wie hier mehrfach illustriert, die Wahrscheinlichkeiten für die ungesehenen Zustände berechnen.

Hier in unserem Beispiel lagen nur binäre Variablen vor und ein Wert war entweder gegeben oder nicht. Bei Variablen mit vielen möglichen Werten kann das beobachtete Vorwissen auch in der Form von vagen Aussagen der Art “Der Würfel zeigte jedenfalls keine 3 und keine 5” vorliegen. Dann gestaltet sich aber die Berechnung aufwändiger.

Es gibt auch Ansätze, die Graphenstruktur soweit wie möglich aus Daten automatisch zu lernen und dann die benötigten Wahrscheinlichkeitstabellen auf der Basis der gefundenen Struktur zu füllen.