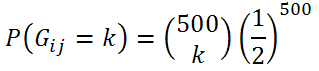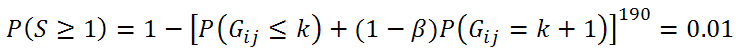Big Data ist das Modewort der Zeit. Daten, die man schon hat, nicht auszuwerten, erscheint kurios, auch wenn es sehr viele sind. Aber wo ist die Grenze? Wie „big“ darf es werden? Wir sind ins Labor gegangen und haben an Zehntausend Zeitreihen Gesetzmäßigkeiten entdeckt, die man in Projekten zu den Themen Big Data und Predictive Analytics kennen sollte.
Höchstwahrscheinlich hat wohl die Verfügbarkeit von billigen Massenspeichern dazu geführt, erst einmal alle anfallenden und beziehbaren Daten zu sammeln, unabhängig davon, ob diese tatsächlich eine Relevanz für das tägliche Geschäft haben werden. Die Angst, möglicherweise gut funktionierende Prädiktoren aus Versehen frühzeitig auszusortieren und sie dann wohlmöglich nicht mehr für die perfekte Formel zur Verfügung zu haben, ist groß.
Wenn unkritisch Unmengen von vorrätigen Datenreihen zur Erklärung von beobachteten Effekten in Betracht gezogen und systematisch auf ihre Prognosefähigkeit getestet werden, schießt man jedoch unter Umständen bei der Analyse über das Ziel hinaus.
Nehmen wir beispielsweise einmal an, dass wir eine monatliche Zeitreihe mit insgesamt 24 Werten über zwei Jahre verfolgen:
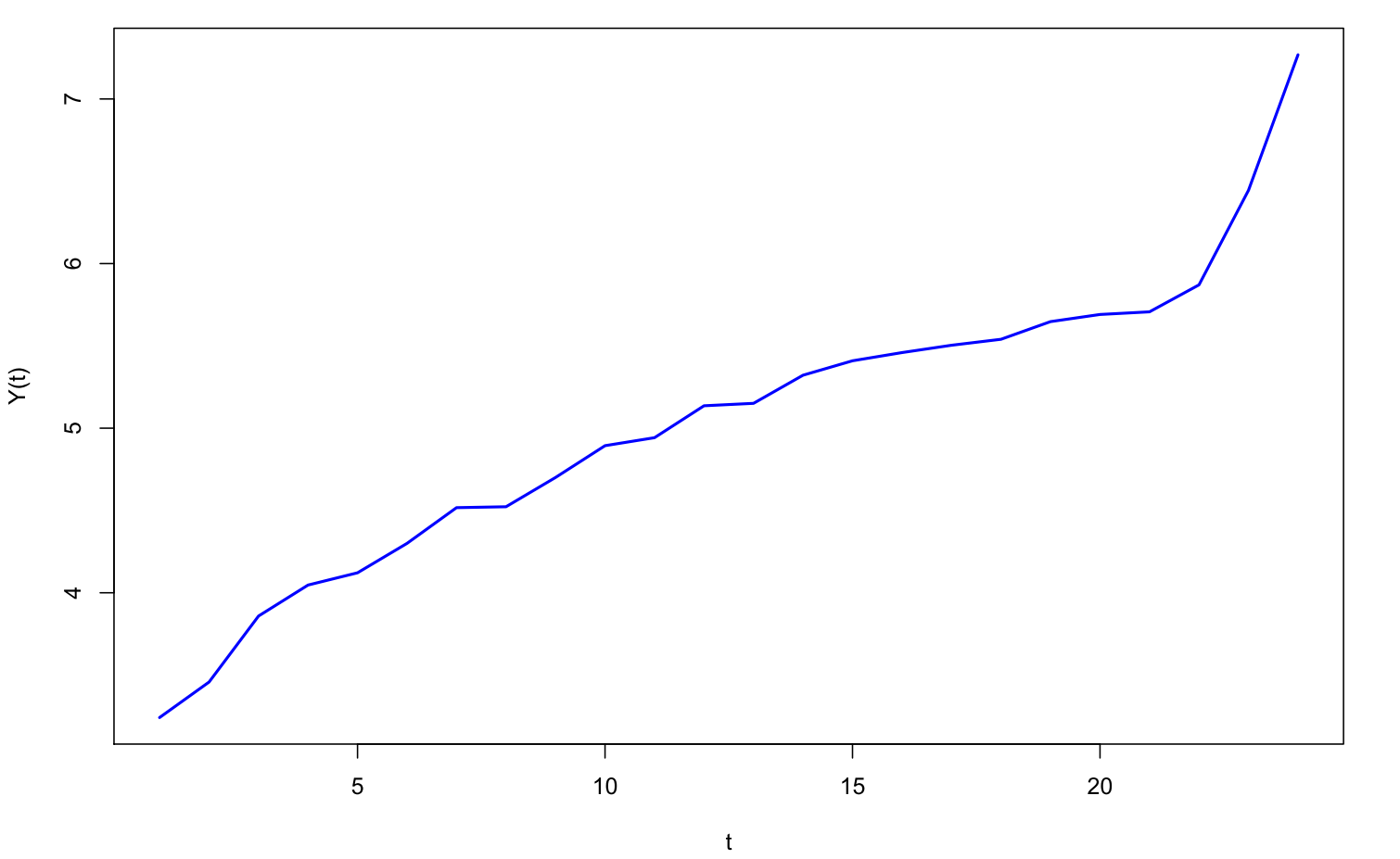
Eine Zeitreihe im Zentrum des Interesses
Weiterhin stellen wir uns vor, dass ein riesiger Pool von Indexzeitreihen zur Verfügung steht. Um einen möglicherweise eingeschlagenen Holzweg noch eindringlicher verdeutlichen zu können, nehmen wir weiterhin an, dass der Pool gar nicht aus realen Zeitreihen besteht, sondern einfach nur unabhängige, identisch normalverteilte Zufallszahlen enthält, die in Segmenten zu jeweils 24 Werten abgerufen werden können. D. h. solchermaßen definierte Zeitreihen haben sogar konstante Erwartung.
Nichtsdestotrotz betrachten wir Korrelationen jeweils zwischen einer Zeitreihe aus dem Pool und unserer gegebenen Zeitreihe. Die Zeitreihe mit der größten Korrelation bei einer Poolgröße von 10000 ist in der folgenden Abbildung in Rot zu sehen, die grüne Zeitreihe zeigt eine mögliche abgeleitete Prognose:
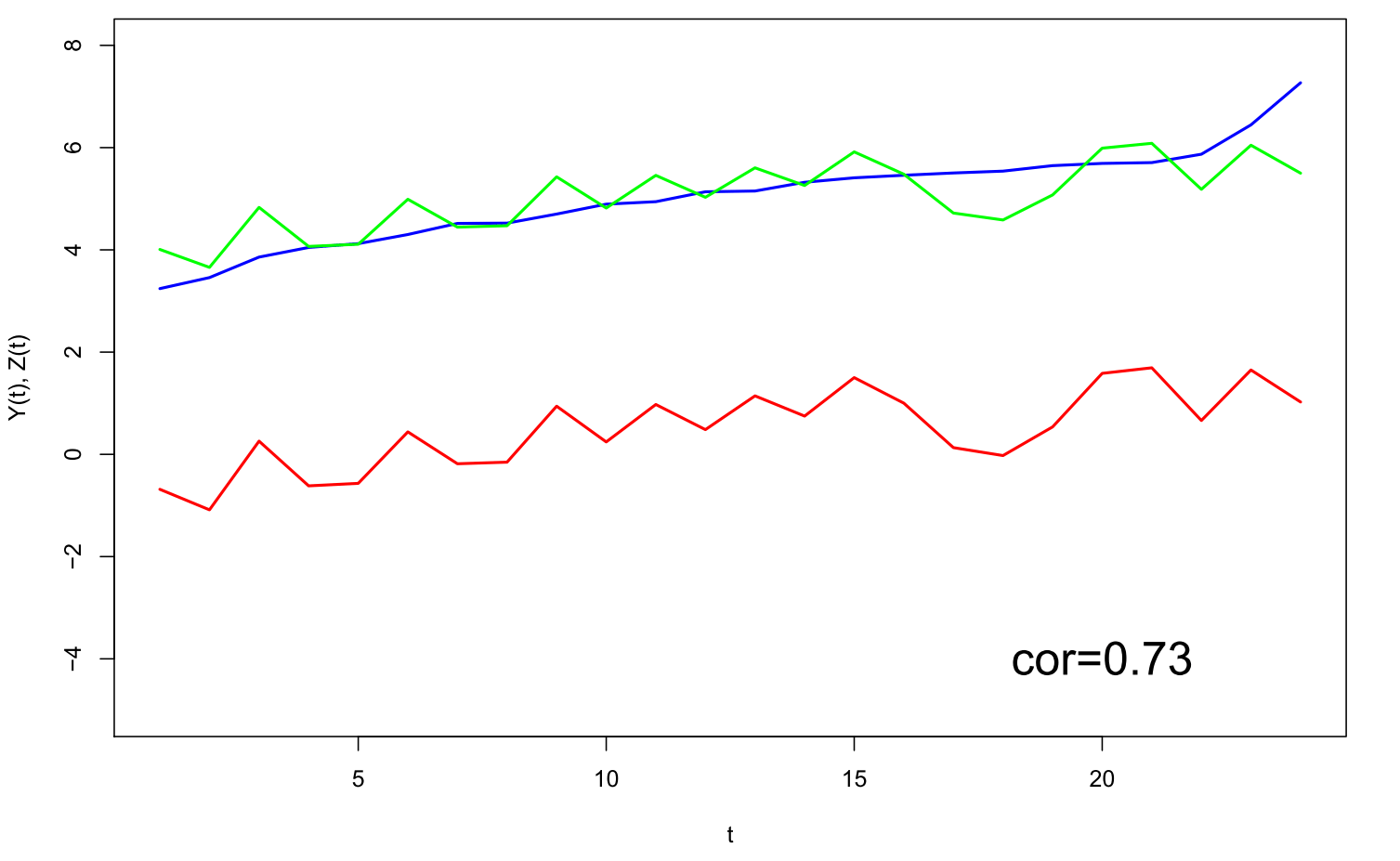
Die beste Zeitreihe (rot) mit einer Korrelation von 0.73 und die abgeleitete Vorhersage (grün)
Eine rein zufällig, ohne systematischen Trend erzeugte Zeitreihe weist somit bereits eine beachtliche Korrelation mit der ausgewählten Zeitreihe auf. Schon an dieser Stelle sollte man im Dunstkreis von Big Data vernommenen Äußerungen, dass Korrelationen Modellbildung ersetzen werden, mit einer gesunden Portion Skepsis begegnen. Eine hohe Korrelation mit einer Indexzeitreihe allein ist somit noch kein hinreichender Grund für einen kausalen Zusammenhang.
Wir könnten ja auch versuchen, mehrere der 10000 Zeitreihen zu verwenden, um unsere uns interessierende Zeitreihe (blau) vorherzusagen. Vier mit einer schrittweisen Prozedur ausgewählte Zeitreihen liefern über eine multiple Regression die folgende Prognose ab:
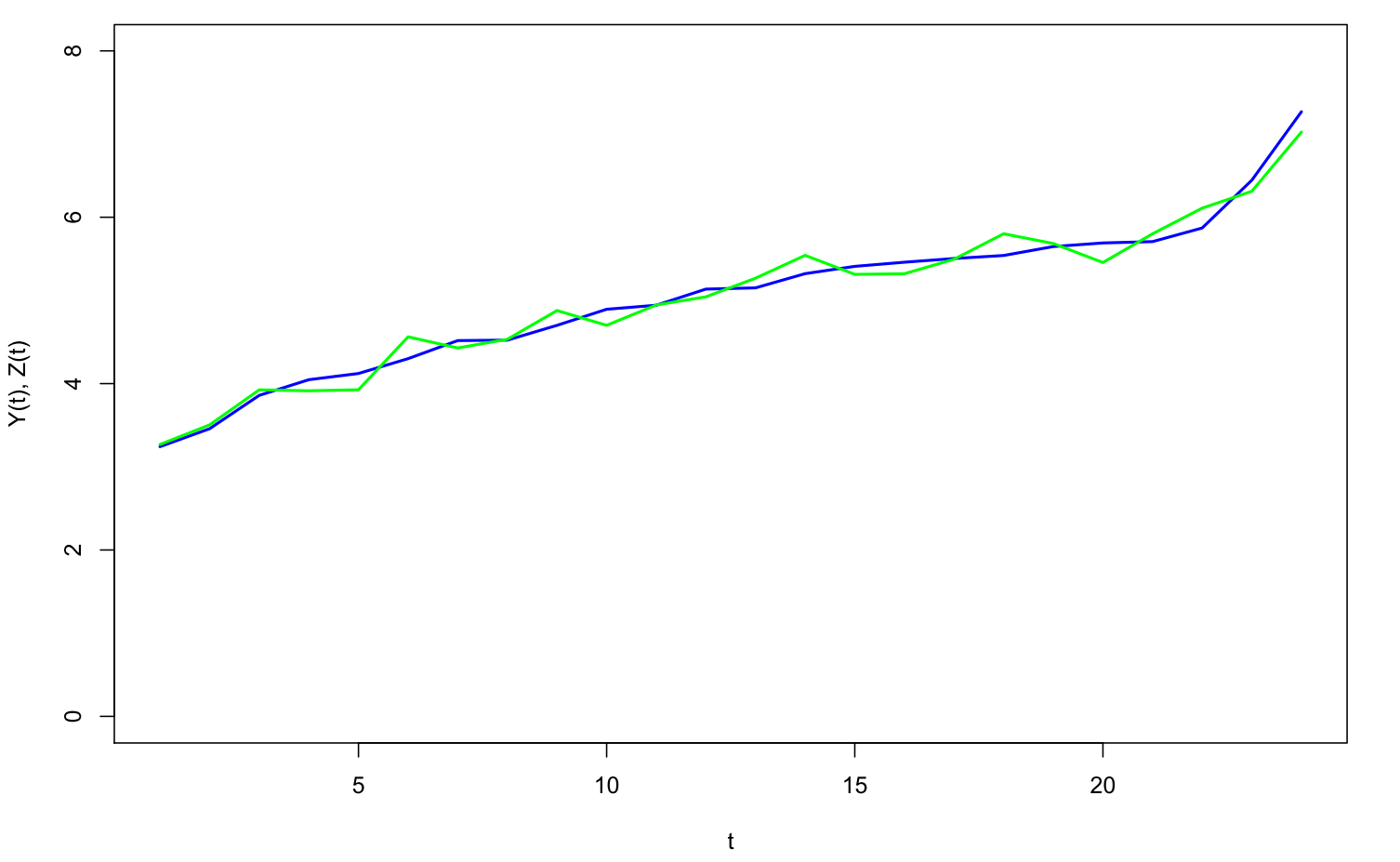
Eine überzeugende Vorhersage (grün) auf der Basis von vier Inputzeitreihen
Es ist schon erstaunlich, welch vermeintliche Prognosekraft Zufallsvektoren zu besitzen scheinen, wenn sie aus einer hinreichend großen Menge ausgewählt werden können. Dass die vermeintliche hohe Prognosegüte nur eine Illusion darstellt, wäre spätestens bei einer Fortsetzung der Prognosen schmerzlich sichtbar geworden.
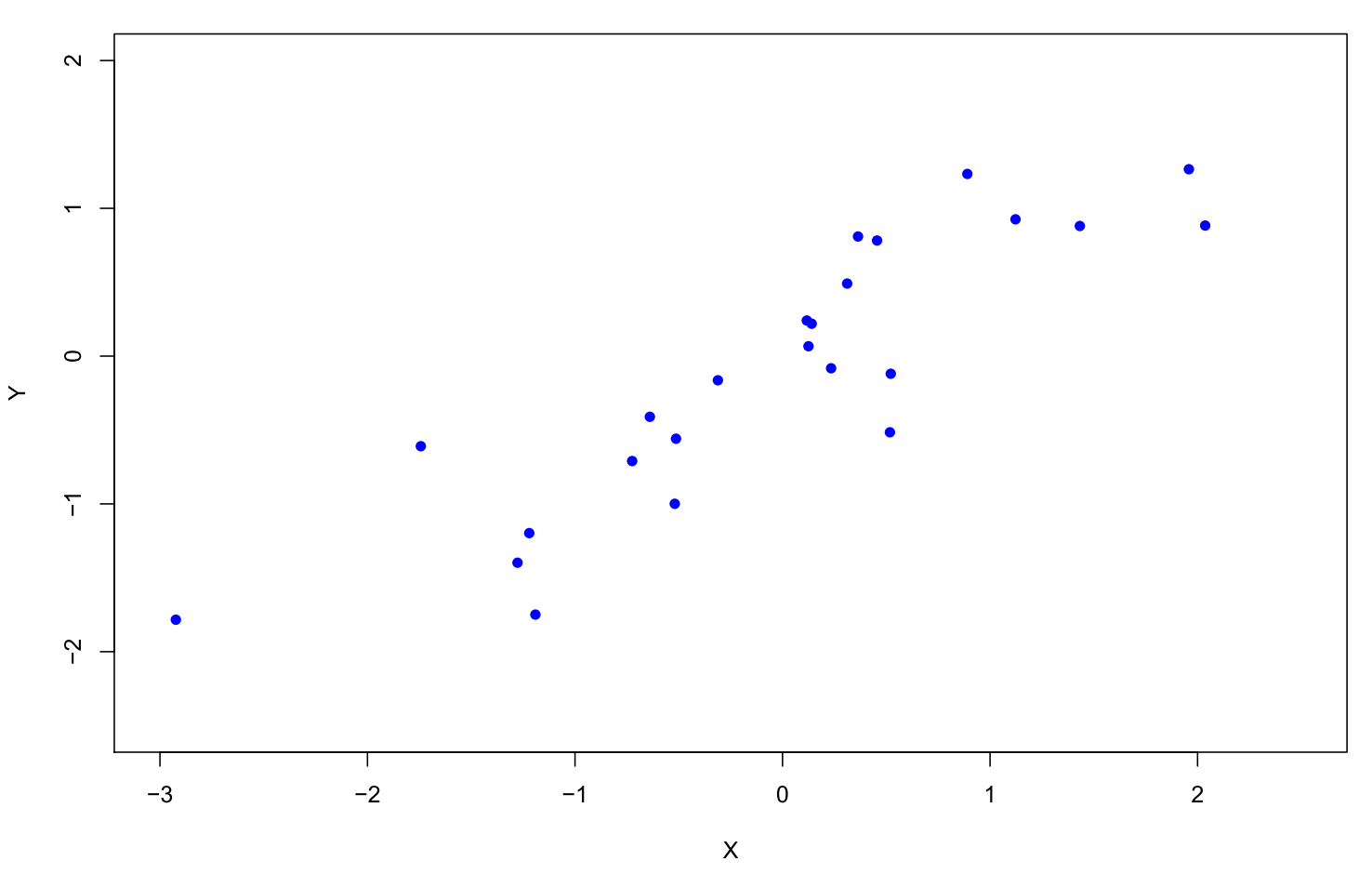
Stellen wir uns nun einmal vor, dass wir unseren Pool von 10000 Zeitreihen auf besonders ähnliche Paare hin durchforsten. Hier wird also jede Zeitreihe mit jeder verglichen. Bei 10000 Zeitreihen ergibt sich somit eine stattliche Anzahl von 10000*(10000-1)/2 = 49.995.000 Vergleichen. Das ähnlichste Paar zeigt im Scatterplot eine sehr strukturierte Punktwolke:
Trotzdem ist auch diese Punktwolke „mit klarem Trend“ nur durch gezielte Selektion aus einer sehr großen Menge mit unstrukturiertem Rauschen entstanden.
Versuchen wir einmal, ein handfesteres Beispiel genauer zu analysieren. Daytrader, die der technischen Analyse vertrauen, suchen gerne nach Regelmäßigkeiten in den Kursverläufen. Hier nehmen wir an, dass wir die qualitativen minütlichen Änderungen des DAX in den ersten 20 Minuten des Handelstages beobachten.
In Wirklichkeit sei das Modell jedoch ein Random Walk, d. h. der DAX steigt oder fällt von Minute zu Minute mit Wahrscheinlichkeit p = 0.5 und dies erfolgt unabhängig von der Historie. Wir haben nun an 500 fiktiven Handelstagen für jedes Paar (i, j) gezählt, wie häufig Änderungen in den Minuten-Intervallen [i-1 ; i] und [j-1 ; j] das gleiche Vorzeichen haben:
![Gleiche Tendenzen beim Paar [1 ; 2] und [2 ; 3] Gleiche Tendenzen beim Paar [1 ; 2] und [2 ; 3]](/images/daxsim.png)
Gleiche Tendenzen beim Paar [1 ; 2] und [2 ; 3]
Wir wissen nicht, von welchen Gefühlen der Daytrader überwältigt wird, wenn er das goldglänzende Kästchen mit satten 282 anstelle der erwarteten 250 Übereinstimmungen bei der Kombination (2, 3), d. h. bei den Intervallen [1 ; 2] und [2 ; 3], erblicken darf.
Wie sollte man dieser Abweichung zur Erwartung begegnen? Dringen wir doch einmal tiefer in die Materie ein.
Für ein festes Paar (i, j) ist die Anzahl der Übereinstimmungen G mit gleichem Trendvorzeichen binomialverteilt:
Hat man sich vor der Datenerhebung ein festes Paar (i, j) ausgesucht und möchte die Hypothese „Es ist ja nur ein Random Walk“ gegen positive Zusammenhänge testen, so ist die Wahrscheinlichkeit für eine Abweichung nach oben in einem einzelnen Paar beispielsweise mit P( G >= 276) ~ 0.01123 bzw. P( G >= 277) ~ 0.00884 gegeben.
Wird somit das Signifikanzniveau alpha = 0.01 vorgegeben, würde man bei 277 oder mehr Übereinstimmungen die Hypothese des Random Walks auf jeden Fall verwerfen, bei 276 Übereinstimmungen (P( G = 276) ~0.00239 ) könnte ein weiteres Zufallsexperiment mit einer auf [0 ; 1] gleichverteilten Zufallszahl Z durchgeführt werden, das bei Z <= 0.484 die Hypothese verwirft, damit das Signifikanzniveau voll ausgeschöpft wird (0.00884 + 0.484 *0.00239 ~0.01 ).
Da das erwähnte Kästchen 282 Übereinstimmungen aufweist und wir somit über der kritischen Grenze liegen, haben wir anscheinend einen bemerkenswerten Zusammenhang gefunden, der sich doch vergolden lassen sollte.
Doch Obacht: Hier haben wir aber 20 * 19 / 2 = 190 Paare, die wir simultan auf Auffälligkeiten untersuchen. Es lässt sich zeigen, dass für p = 0.5 die Anzahlen der Übereinstimmungen in den Paaren (i, j) und (j, k) trotz des gemeinsamen Index j unabhängig verteilt sind. Zunächst folgt sowieso, dass auch bei einem Random Walk 190 * 0.01 ~ 2 Auffälligkeiten erwartet werden können, obwohl es eigentlich nichts zu sehen gibt. Wir können sogar die Wahrscheinlichkeit, mindestens ein signifikantes Ergebnis zu erhalten, wegen der genannten Unabhängigkeit exakt berechnen:
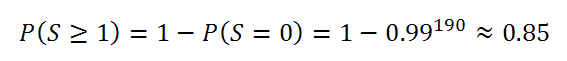
In 85 % aller Fälle „ist da irgendetwas“.
Augenscheinlich führt ein naives Vorgehen zu ständigen Fehlalarmen: In 85 % aller Fälle sehen wir mindestens ein Paar, für welches die beobachtete Trendübereinstimmung über unserer kritischen Grenze liegt – obwohl in Wirklichkeit keinerlei Zusammenhang besteht.
Um nicht auf solche durch „große“ (190 ist da noch relativ klein) Anzahlen von unabhängigen Tests gefundenen Auffälligkeiten reinzufallen, muss das Signifikanzniveau eines einzelnen Tests angepasst werden. Wir hätten gerne erreicht, dass bei einem Random Walk die Wahrscheinlichkeit, überhaupt mindestens eine Auffälligkeit – über alle 190 Paare hinweg – zu entdecken, alpha = 0.01 betragen soll. Hierzu ist die Gleichung
zu lösen. Nach etwas Rechnerei ergibt sich, dass bei einem Wert von k = 294 und mehr die Hypothese eines Random Walks auf jeden Fall verworfen wird, für jedes Paar (i, j) mit k = 293 wird noch eine gleichverteilte Zufallszahl Z erzeugt und die Hypothese dann verworfen, wenn Z <= 0.22436 ist. Mit diesem Vorgehen wird die Nullhypothese bei tatsächlichem Vorliegen eines Random Walks mit exakt p = 0.01 verworfen.
Nun wird ersichtlich, dass das güldene Feld von oben mit k = 282 noch überhaupt keinen Anlass geben kann, nervös zu werden. Die hohe Abweichung nach oben ist normal, wenn so viele Paare auf einmal betrachtet werden.
Es sollte deutlich geworden sein, dass eine große Anzahl von untersuchten Modellen bzw. von parallel durchgeführten Analysen bei der Auswertung nicht unberücksichtigt bleiben darf. Die Kriterien, die die Relevanz eines Ergebnis bewerten, müssen immer – wie im beschriebenen Beispiel illustriert – an die Rahmenbedingungen angepasst werden.