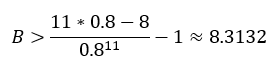Ob Seminare oder Flüge gebucht werden – selten erscheinen wirklich sämtliche angemeldeten Personen zum Kurs bzw. Flug. Es liegt nahe, die potenziellen No-Shows bereits bei der Annahme der Buchungen zu berücksichtigen. Wie das geht, verraten wir heute!
Nehmen wir einmal an, dass wir im Oktober 2017 ein Seminar veranstalten wollen. Bereits im Februar 2017 werden die Anmeldungen angenommen. Damit die Qualität des Seminars hochgehalten wird, ist die Kapazität auf 10 beschränkt. Langjährige Erfahrungen zeigen, dass etwa 80% der angemeldeten Personen auch tatsächlich erscheinen. Nun gibt es 17 Interessenten.
Wie vielen der Interessenten sollte eine Zusage zur Teilnahme gegeben werden?
Um diese Frage mit Methoden der Predictive Analytics beantworten zu können, sollten wir die Modellannahmen und die verwendeten Parameter näher betrachten. Die Kapazitätsgrenze M = 10 hatten wir bereits erwähnt.
Weiterhin nehmen wir an, dass erst am Tag des Seminars nur von einem dann tatsächlich erscheinenden Teilnehmer die Gebühr G auch eingezogen wird. Das Risiko eines No-Shows liegt somit bei uns. Alternativ könnten wir annehmen, dass die Gebühr sofort erhoben wird und das Risiko auf den Kursteilnehmer übergeht, aber hier tun wir so, als ob wir die schwächere Position inne hätten.
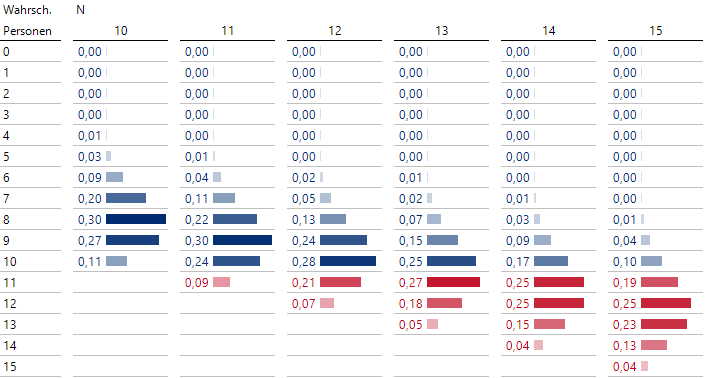
Wahrscheinlichkeiten für die Anzahl der tatsächlich erscheinenden Personen, wenn N angemeldet werden
Andererseits wird jede erscheinende Person, die keinen Platz mehr findet, unser Image negativ beeinflussen. Wir setzen für jeden erscheinenden Kandidaten ohne Platz im Seminar einen negativ zu verbuchenden Betrag B an. Eine bereits im Februar erfolgte zeitnahe Absage an einen Interessenten wird als unkritisch und ohne Auswirkung auf unser Ansehen eingeschätzt.
Eine letzte wichtige Annahme ist, dass das Erscheinen eines Teilnehmers von den Entscheidungen der übrigen Kandidaten unbeeinflusst bleibt. Es gibt in unserem Modell auch keinen Platz für einen externen Grund, wie etwa ein schweres Unwetter, der für die simultane Abwesenheit mehrerer Kursbesucher verantwortlich sein kann.
Die obige Tabelle zeigt für verschiedene Werte N von angemeldeten Personen die Wahrscheinlichkeiten, dass eine bestimmte Anzahl von Personen auch tatsächlich zum Seminar antreten will.
Die zugrundeliegenden Wahrscheinlichkeiten können mittels Binomialverteilungen ausgerechnet werden. Die Fälle, bei denen mehr Personen erscheinen als Plätze vorhanden sind, sind hier rot eingefärbt. Wenn nur 10 Personen angemeldet werden, reicht die Kapazität natürlich sicher aus. Ab 11 und mehr angemeldeten Personen besteht aber die grundsätzliche Gefahr, dass dann auch 11 oder mehr Personen erscheinen und der vorhandene Platz nicht für alle Anwesenden ausreicht.
Trotzdem kann es sich lohnen, Überbuchung zuzulassen!
Im folgenden Diagramm zeigen wir die möglichen Nettobeiträge dieses Seminars, die bei N Anmeldungen und den jeweils tatsächlich erscheinenden Personen möglich sind. Jede Person, die im Kurs untergebracht werden kann, erzeuge einen positiven Beitrag von G = 1, während jede Person, die keinen Platz mehr findet, einen Abzug von B = 4 verursache.
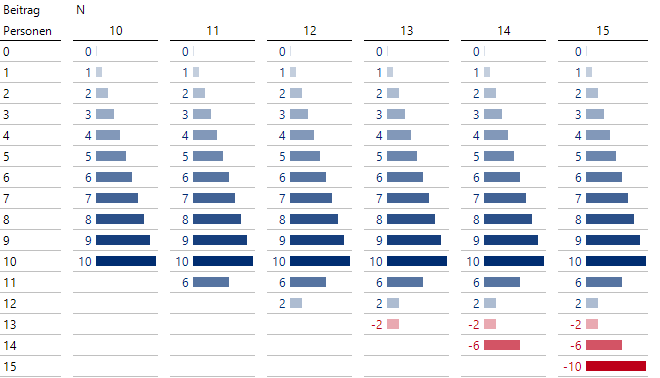
Nettobeiträge in Abhängigkeit von der tatsächlichen Personenanzahl
Wenn beispielsweise 13 von N = 14 angemeldeten Personen erscheinen, können 10 am Seminar teilnehmen und 3 müssen nach Hause geschickt werden. Der Nettobeitrag ergibt sich somit zu 10 * 1 – 3 * 4 = -2 und ist hier sogar negativ.
Um beurteilen zu können, wie relevant ein Nettobeitrag ist, muss er mit der Wahrscheinlichkeit aus der ersten Tabelle gewichtet werden. Es ergibt sich dann die folgende Tabelle:
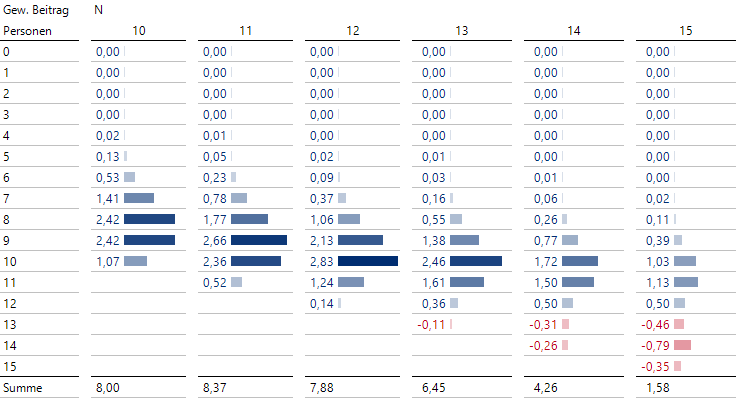
Berechnung der erwarteten Nettobeiträge
Die Summe dieser gewichteten Beiträge pro Spalte ergibt den erwarteten Nettobeitrag und ist für jedes N unterhalb der jeweiligen Spalte angegeben.
Nun lässt sich für jede mögliche Anzahl von Anmeldungen wie beschrieben der erwartete Nettobeitrag berechnen. Für eine Anzahl von Anmeldungen X unterhalb der Kapazitätsgrenze ist die Erwartung einfach X * 0.8. Es lohnt sich somit schon einmal, mindestens Anmeldungen in Höhe der Kapazitätsgrenze zuzulassen.
Wie ersichtlich ist, liegt der erwartete Wert mit 8.37 für N = 11 angemeldete Personen höher als z. B. die erwarteten 10 * 0.8 = 8 für N = 10 Anmeldungen.
Die folgende Grafik zeigt den Gesamtverlauf des erwarteten Nettobeitrags für mögliche Anmeldungsanzahlen N von 0 bis 20:
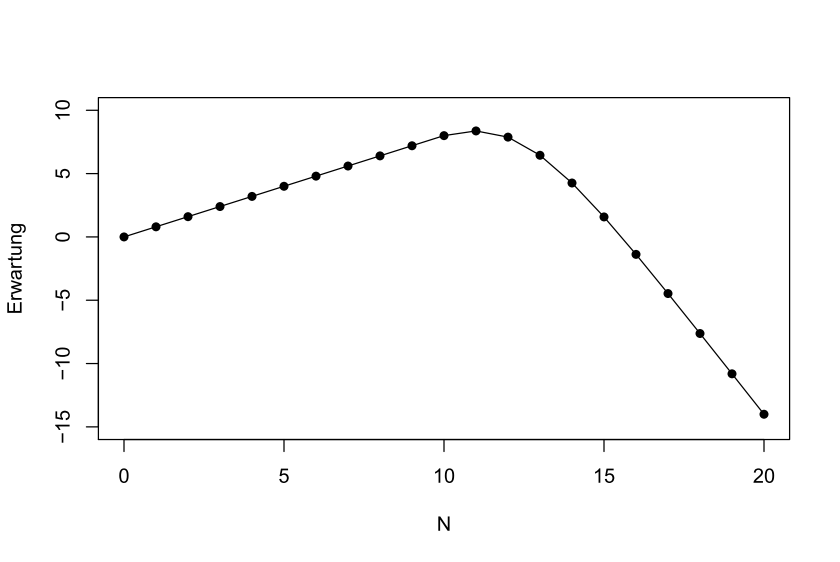
Verlauf der erwarteten Nettobeiträge für verschiedene Anmeldungsanzahlen N
Bis N = 10 steigt die Erwartung linear, dann wird das Maximum bei N = 11 angenommen und für größere Werte von N sinkt die Erwartung wieder. In diesem konkreten Fall (M = 10, p = 0.8, G = 1, B = 4) lohnt es sich somit, ruhig 11 Personen anzumelden, da dann der erwartete Nettobeitrag maximiert wird. Aus betriebswirtschaftlicher Sicht ist es somit durchaus zielführend, über die Kapazität hinaus Personen anzumelden.
Ob überbucht werden sollte, hängt aber unter anderem auch von der Höhe der Bestrafung B ab. Nun wollen wir einmal den Wert von B variieren und jeweils die Erwartungen bei 10 bis 15 Anmeldungen berechnen. Die maximale Erwartung und die zugehörige Anmeldungsanzahl sind in den letzten beiden Spalten der folgenden in DeltaMaster berechneten Tabelle angegeben. Die Zeile zum Kurs B2 gehört zu unserem obigen Beispiel mit B = 4:
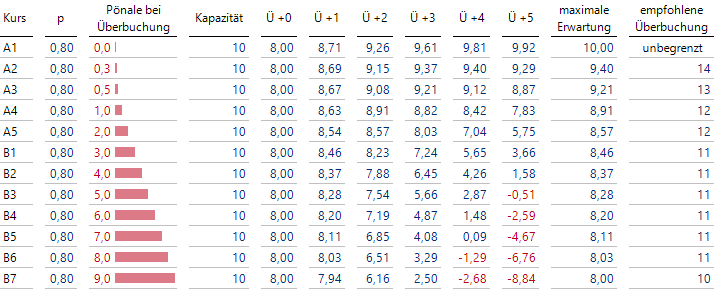
Berechnung der optimalen Überbuchungsanzahlen für diverse Werte der Pönale B
Betrachten wir einmal die erste Zeile, bei der keine Bestrafung anfällt (B = 0). Mit der Anmeldungsanzahl wächst auch die erwartete Anzahl der tatsächlich Eintreffenden. Da überzählige Anwesende nicht negativ in die Berechnung eingehen, kann es nie genug Anmeldungen geben. Der erwartete Beitrag des Kurses nähert sich dann der 10, da mit einer an 1 grenzenden Wahrscheinlichkeit mindestens 10 Personen erscheinen werden und der Kurs somit komplett besetzt ist und gleichzeitig überzählige Anwesende ohne Nachteil nach Hause geschickt werden können.
Wird nun die Pönale erhöht, lohnt es sich immer weniger, Überbuchungen zu betreiben und die empfohlene Überbuchungsanzahl sinkt. Irgendwann, genauer gesagt, wenn
ist, überwiegt die hohe Strafe bei Überbuchung den möglichen Vorteil und es wird dann empfohlen, die Kapazität auszuschöpfen, aber nicht zu überschreiten. Deshalb wird im Kurs B7 mit B = 9 nicht überbucht und die Anmeldungsanzahl bei der Kapazität M = 10 belassen.
Hat man nun mehrere Seminare im Angebot, mit möglicherweise unterschiedlichen Kapazitäten und Anwesenheitsquoten, dann lässt sich für jede Konstellation die optimale Anmeldungsanzahl ermitteln, die den erwarteten Nettobeitrag maximiert (B kann natürlich auch noch variieren, aber hier sei durchgehend B = 4):
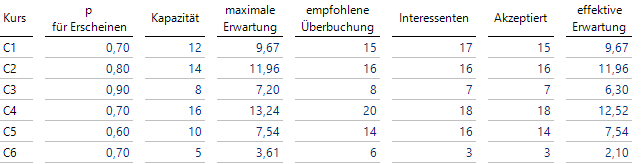
Berechnung der akzeptierten Anmeldungen
Gibt es mehr Interessenten als die empfohlene Überbuchung, müssen einige Personen vertröstet werden (Seminare C1 und C5).
Der Vollständigkeit halber sei noch der Fall erwähnt, dass gar nicht so viele Interessenten erscheinen, wie es der empfohlenen Überbuchung entspricht. In solchen Fällen werden alle Interessenten akzeptiert, auch wenn dann der effektive erwartete Nettobeitrag niedriger ausfällt (Seminare C3, C4 und C6).
Hier waren die Quoten p für das Erscheinen bereits gegeben. Zu einer vollständigen Predictive-Analytics-Anwendung könnte noch die Erstellung eines Modells gehören, das dieses p für diverse gegebene Rahmenparameter des Seminars (z. B. Thema, Referent, Ort, Jahreszeit usw.) vorhersagt.
Deutlich komplexer werden die Analysen, wenn sich die Anmeldungen über einen längeren Zeitraum hinziehen und die Wahrscheinlichkeiten des späteren, tatsächlichen Erscheinens auch vom Zeitpunkt der Anmeldung abhängen. Möglicherweise ist eine exakte Ableitung wie oben dann zu komplex – in diesem Falle können dann Simulationen helfen.