Oft verhalten sich Zeitreihen für eine Weile relativ stabil und schwanken um einen konstanten Wert, um dann auf ein neues Niveau zu steigen oder zu sinken. Unter gewissen Annahmen können diese Niveauänderungen von einem Algorithmus selbstständig erkannt und automatisch Zeiträume gleichen Niveaus generiert werden.

Wir hatten bereits in Zeitmustererkennung: Segmentierung von Niveauänderungen in Zeitreihen einen Algorithmus vorgestellt, der eine einfache Zeitreihe mit einer Beobachtung pro Zeitpunkt segmentiert. Dort musste allerdings die Anzahl der Segmente vorgegeben werden.

Um zu verstehen, welche Information fehlt, um auch auf die Vorgabe der Anzahl der Segmente verzichten zu können, betrachten wir eine einfache Zeitreihe, die aus sechs Werten besteht:

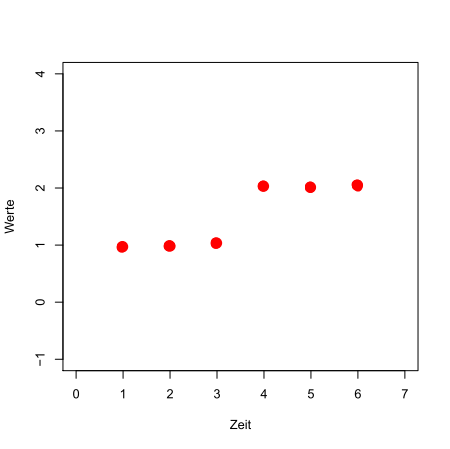
Eine simple Zeitreihe mit sechs Beobachtungen

Es sieht so aus, als ob nach drei Beobachtungen ein Sprung stattgefunden hat. Doch immer der Reihe nach …

Ein mögliches passendes Zeitreihenmodell ist

y(t) = M(t) + e(t)

Der zu einem Zeitpunkt t beobachtete Zeitreihenwert y(t) wird dargestellt als Summe aus dem wahren Wert M(t), der uns interessiert, aber leider unbekannt ist, und einem Fehler e(t). Von diesem Fehler nimmt man an, dass er um den Wert 0 mit einer normalerweise ebenfalls unbekannten Varianz schwankt.

Wären der Fehler und somit auch die Varianz zu jedem Zeitpunkt immer 0, könnte man anhand der Beobachtungen mit absoluter Sicherheit entscheiden, ob aufeinanderfolgende Werte M(t) und M(t+1) auf einem Niveau liegen oder nicht. Wären in unserem obigen Beispiel die Werte ohne Fehler, so gäbe es nicht nur nur zwischen dem dritten und viertem Wert einen Sprung, sondern auch bspw. einen kleineren zwischen dem zweiten und dem dritten Wert. Konsequenterweise unterscheiden wir zwischen der Tatsache, dass sich Werte unterscheiden und dem Betrag der Abweichung. Bei einer angenommenen Varianz von 0 hat sich das Niveau M(t) zwischen t=2 und t=3 sicher geändert, aber eben nur um einen winzigen Betrag.

Wir möchten nun nicht wissen, ob sich der Wert y(t) verändert hat – das sehen und messen wir – sondern, ob es vorteilhafter ist anzunehmen, dass sich M(t) verändert hat oder nicht. Ein Mittelwert, der über mehrere Zeitpunkte eines Intervalls gebildet wird, ist stabiler; andererseits wird möglicherweise ein Bias, ein systematischer Fehler generiert, wenn die zusammengelegten Werte M(t) in diesem Intervall voneinander abweichen. Die Varianz des Fehlers ist hier die entscheidende Größe, um den Effekt des Zusammenlegens beurteilen zu können.

Liegt nun wie oben jedoch nur eine Beobachtung pro Zeitpunkt vor, kann ohne weitere Annahmen nicht beurteilt werden, wie sich der beobachtete Wert y(t) auf den theoretischen Wert M(t) und den Fehler e(t) aufteilt und somit kann auch die Varianz nicht vernünftig geschätzt werden.

Ohne zusätzliche Annahmen gelangt man nun somit nicht zu einer befriedigenden Schätzung der Fehlervarianz. Welche Möglichkeiten bleiben? Manchmal hilft ein parametrisches Modell für M(t), z.B. eine angepasste Gerade, das auch bei nur einer Beobachtung pro Zeitpunkt die Schätzung der Varianz ermöglicht. Bei unserer Annahme konstanter Werte auf einer unbekannten Anzahl von Intervallen mit variablen Grenzen ergeben sich jedoch bei der üblichen Minimierung der Fehlerquadratsumme pathologische Lösungen, da eine Einteilung mit nur einem Zeitpunkt pro Intervall immer zu einem Gesamtfehlerwert von 0 führt.

Am einfachsten wäre es sicher, den Wert der Varianz vom Anwender festlegen zu lassen. Die Möglichkeit, die wir hier nun beschreiben möchten, ist datengetrieben und geht davon aus, dass der beobachtete Wert selbst ein Mittelwert aus mehreren unabhängigen Wiederholungen ist. Es könnte sich beispielsweise um die Benzinpreise einer zufälligen Auswahl von Tankstellen handeln und uns interessiert der Durchschnittspreis.

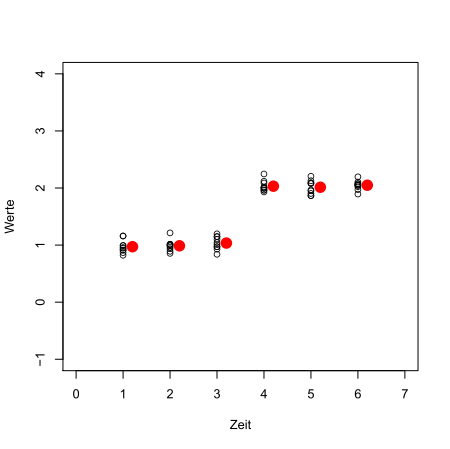
10 Wiederholungen pro Zeitpunkt, zusammen mit dem Mittelwert

Die Wiederholungen erlauben nun eine Schätzung der Varianz und diese liefert wiederum die Grundlage für unseren Algorithmus zu entscheiden, ob eine Zusammenlegung von Intervallen die erwartete Stabilität der Darstellung erhöhen wird.

In der vorliegenden Variante nimmt der Algorithmus eine gleichbleibende Größenordnung der Streuung im Zeitverlauf an. Er verwendet Methoden der Modellauswahl und ermittelt die global optimale Aufteilung in Segmente. Für eine flotte Berechnung werden Ansätze der Dynamischen Programmierung eingesetzt.

Für unser Beispiel sehen wir die plausible Einteilung in zwei Dreiergruppen, die auch unser Algorithmus findet. Die gewonnene Stabilität durch Mittelwertbildung über drei Zeitpunkte ist höher einzuschätzen als der Informationsverlust durch Glättung möglicherweise leicht verschiedener Werte M(t).

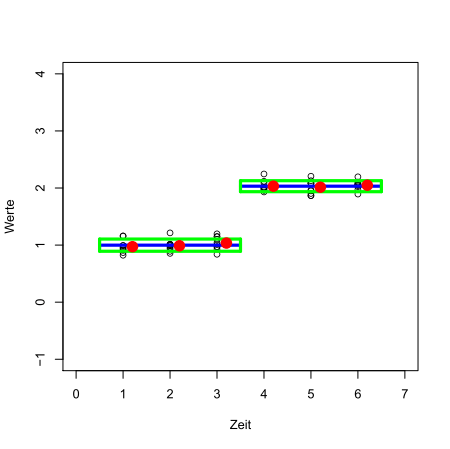
Automatisch gefundene Einteilung in zwei Dreiergruppen

In der Grafik werden Mittelwerte (blau) +/- Standardabweichungen (grün) der gefundenen Segmente dargestellt. Erhöht sich die Streuung, so fällt es immer schwerer zu entscheiden, ob sich die Erwartung, also M(t) geändert hat oder nicht, und welche Zeitpunkte zusammengefasst werden können:

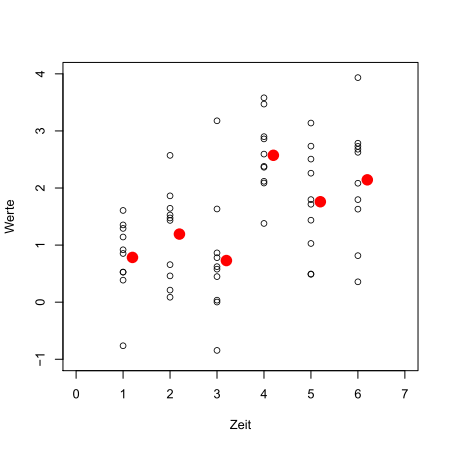
10 Wiederholungen pro Zeitpunkt, diesmal mit größerer Streuung

Unser Algorithmus findet vollautomatisch eine geeignete Einteilung mit der sich dadurch ergebenden Anzahl von Abschnitten. Im vorliegenden Beispiel sind es drei Segmente.

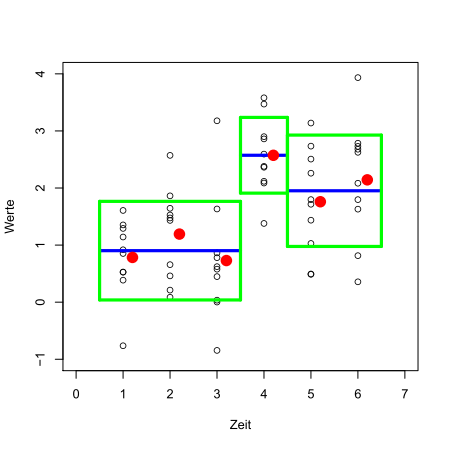
Automatisch gefundene Einteilung in drei Segmente

Der Algorithmus hat dem Zeitpunkt 4 ein eigenes Intervall gegönnt, da die beobachteten Werte (zufällig!) etwas weiter nach oben abwichen.

Wir stellen uns z.B. eine interaktive Anwendung vor, die zur visuellen Unterstützung das zugehörige Intervall hervorhebt:

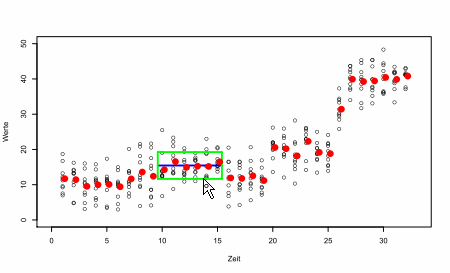
Mögliche interaktive Anwendung

Hier hatten wir uns auf Zeitreihen konzentriert, deren konstantes Niveau sich von Zeit zu Zeit ändert. Was passiert, wenn es auch lineare Trends geben kann? Dazu an dieser Stelle später mehr.