Der Streit um das richtige Vorgehen in der Corona-Krise bleibt weiterhin Schwerpunktthema in Regierungen, Forschungseinrichtungen und an virtuellen Stammtischen. Im heutigen Beitrag versuchen wir wieder, die aktuelle Lage etwas klarer zu erfassen.
Obwohl ich mir eigentlich fest vorgenommen hatte, dieses Mal ein Thema abseits von Corona zu wählen, habe ich mich den laufenden Monat de facto doch wieder nahezu ausschließlich mit Veröffentlichungen zu Covid-19 beschäftigt, sei es in der Wissenschaft oder in der Tagespresse.
Wo steckt die Basisreproduktionszahl im SIR-Modell (Beta=0.5, Gamma=0.2)?
Vorabversionen von wissenschaftlichen Artikeln, die noch nicht das Peer-Review durchlaufen haben (das dann wenigstens ein gewisses Niveau an Anspruch sichert!), und die Tendenz der Medien, aus diesen ausgewählte „Erkenntnisse“ ohne zeitliche Verzögerung im günstigsten Fall verkürzt wiederzugeben, aber im Normalfall – zumindest in den Clickbait-Überschriften – aus dem Zusammenhang zu reißen, ergeben eine gefährliche Kombination. Expertenäußerungen können hierbei ersatzweise die Rolle der Artikel übernehmen.
Kommen noch die jeweils lauernden Fangruppen ins Spiel, immer bereit, die „richtigen“ Ergebnisse sofort in den sozialen Netzwerken und in Kommentarspalten zu verbreiten und zu vervielfachen, führt dies zu einem Gesamtrauschen, das kein klares Informationssignal mehr enthält. Dann spielt es später auch keine große Rolle mehr, wenn ein Artikel unter dem Radar korrigiert oder sogar zurückgezogen wird, oder der Experte beteuert, dass er nicht korrekt zitiert wurde.
Zumindest bei mir führt dieses Rauschen dazu, mir doch lieber immer einen Artikel selbst anzuschauen und mich für eine bessere Beurteilung gegebenenfalls in die Materie einzulesen, auch wenn es natürlich Zeit kostet. Sie können mir hier gerne über die Schulter schauen!
Ein Begriff, der die letzten Wochen eine größere Rolle gespielt hat, ist die Basisreproduktionszahl R0. Mit Reproduktionszahlen konnte man wahlweise beweisen, dass man eindeutig auf dem richtigen Weg sei oder alternativ, dass der Lockdown doch offensichtlich überflüssig war. Ihnen sind sicherlich bereits Diagramme wie das obige begegnet, das den dynamischen Verlauf der Bestandszahlen von Infizierten oder auch noch nicht Betroffenen in einer Gesamtbevölkerung gemäß einem mathematischen Modell (hier handelt es sich um ein deterministisches SIR-Modell) beschreibt.
Was besagt nun diese Basisreproduktionszahl? Häufig wird die Antwort genannt, dass es sich um die durchschnittliche Anzahl der zusätzlichen Personen handelt, die ein Infizierter während seiner infektiösen Phase zu Beginn einer Epidemie in einer nicht immunen Gesellschaft ansteckt. Im Schnitt gibt es somit für einen Infizierten R0 neue Infizierte, wenn die infektiöse Phase der ausgewählten Person beendet ist. Diese stecken ihrerseits gemäß diesem Muster weitere Personen an und zwar auch schon möglicherweise, bevor die infektiöse Phase der Ausgangsperson beendet ist.
Es handelt sich hierbei nicht um eine reine Naturkonstante, die nur von der Krankheit abhängt, sondern für die Basisreproduktionszahl spielt beispielsweise auch das übliche, „normale“ Verhalten der Bevölkerung eine Rolle.
Es lohnt sich, das SIR-Modell (und seine Erweiterungen) zu studieren, um Epidemie-Entwicklungen abschätzen zu können, immer natürlich unter der Annahme, dass das SIR-Modell die Wirklichkeit hinreichend genau wiedergibt.
Vergessen wir einmal Fallzahlen und Verdopplungsintervalle und schauen auf die Bestandteile des SIR-Modells:
- Wir verwenden eine Beschreibung mit Anteilen an der Gesamtbevölkerung:
- Zu einem Zeitpunkt t gibt es die folgenden Größen, meist Abteilungen („compartments“) genannt:
- S = s(t) („susceptibles“): Dies ist der Anteil der Personen, die für einen Virus anfällig sind und sich gegebenenfalls infizieren könnten.
- I = i(t) („infected“): Dies ist der Anteil der Personen, die gerade infiziert sind.
- R = r(t) („removed“): Dies ist der Anteil der Personen, die die infektiöse Phase überstanden haben und in diesem Modell nicht mehr infiziert werden können. Ein bestimmter Anteil der R-Abteilung ist immun, der restliche Anteil verstirbt. Bei aktivem Handeln könnte auch eine absichtliche Isolierung von Infizierten dazugehören.
- Die Summe der drei Anteile ist immer S + I + R = 1, es gibt keine sonstigen Geburten oder Todesfälle.
- Die Reihenfolge der möglichen Übergänge ist fest durch S → I → R gegeben, d. h., ein „susceptible“ kann sich infizieren (oder auch nicht) und ein „infected“ verwandelt sich womöglich in ein „removed“. Es gibt aber keine Abkürzungen oder Zurückführungen zu früheren Zuständen.
- Für den Zeitpunkt t=0 gibt es eine Anfangsverteilung der drei Abteilungsanteile. Kehren etwa 100 Infizierte aus dem Skiurlaub zurück in das noch virenfreie Deutschland mit angenommenen 83 Mio Einwohnern, so könnten die Anteile lauten:
s(0) = 82.999.900/83.000.000, i(0) = 100/83.000.000 und r(0) = 0 - Das R0 hat nichts mit dem R = r(t) zu tun; das eine steht für „reproduction“, das andere für „removed“.
- Das I = i(t) sollte man nicht mit den Neuinfizierten eines Tages verwechseln, sondern I ist eine Bestandsgröße.
Die Zeit verläuft kontinuierlich und die Dynamik wird durch die folgenden Differentialgleichungen beschrieben:
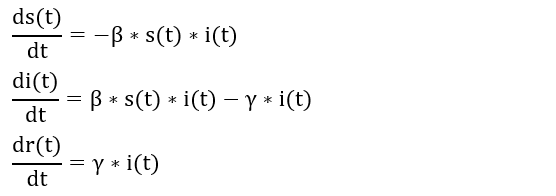
Dynamik des SIR-Modells
Gesucht sind drei Funktionen (in der obigen Abbildung wurden sie schon numerisch gefunden) s(t), i(t) und r(t), sodass die Gleichungen zu jedem Zeitpunkt t erfüllt sind. Sie stellen dabei Steigungen (die linken Seiten) zu Funktionswerten (die rechten Seiten) in Beziehung.
Die Gleichungen beschreiben Gesetzmäßigkeiten, etwa wie Infizierungen stattfinden oder wie die infektiöse Phase beendet wird.
Wir fangen mit der ersten Gleichung an: Eine Neuinfektion kann nur dann stattfinden, wenn ein Infizierter auf einen „susceptible“ trifft. Das Produkt der Anteile s(t)*i(t) ist proportional zur Wahrscheinlichkeit, dass ein zufälliges Aufeinandertreffen zweier Personen zu dieser Konstellation gehört. Hier nimmt man also an, dass die Abteilungen S, I und R gut durchmischt und nicht etwa räumlich getrennt sind.
Besonders hoch wäre das Produkt, wenn die Bevölkerung jeweils zur Hälfte aus Infizierten und aus Empfänglichen bestünde. Gibt es keine Infizierten, passiert nichts, und sind alle bereits infiziert oder immun, gibt es auch keinen weiteren Zuwachs.
Der Parameter Beta steuert dabei, wie leicht es bei einem Kontakt zur Übertragung des Virus kommt.
Der Anteil, der von S abgezogen wird, wandert zur Abteilung I.
Könnte man die Neuinfektionen schlagartig unterbinden und gäbe es somit keinen Zuwachs aus der S-Abteilung, erhielte man eine exponentiell fallende Funktion I(t). Hier ist die Interpretation des Parameters „Gamma“ einfacher: Der Kehrwert von „Gamma“ ist gleich der durchschnittlichen Dauer der Infektiosität.
Schauen wir auf den SARS-CoV-2-Steckbrief des RKI, Punkt 5, heißt es dort allerdings „Das Ende der infektiösen Periode ist momentan nicht sicher anzugeben.“. In einer sehr kleinen Studie sei eine Ende der Infektiosität etwa 4 Tage (Rachen), bzw. 8 Tage (Sputum) nach Symptombeginn festgestellt worden.
Wir behalten außerdem im Hinterkopf, dass ein Infizierter im Gegensatz zu den Annahmen des SIR-Modells nicht sofort selbst infektiös ist, aber bereits 2 Tage vor den ersten Symptomen. Am höchsten sei die Ansteckungsgefahr am Tag vor den ersten Symptomen. Die Inkubationszeit wird mit Mittel mit 5 – 6 Tagen angegeben (Spannweite ist allerdings 1 – 14), daher sollte etwa bei 4 – 5 Tagen die Gefahr für eine Weiterverbreitung maximal sein.
Aber kehren wir zurück zu den Differentialgleichungen: Falls Sie sich an Ihre Schulzeit erinnern, wurde die Steigung einer Funktion als Grenzwert des Differenzenquotienten definiert. Genauso lässt sich ein System von Differentialgleichungen, falls man es nicht explizit lösen kann, häufig durch ein System von Differenzengleichungen beliebig genau annähern.
Geht man in genügend kleinen Zeitschritten vor, lässt sich aus diesem System eine numerische Näherungslösung konstruieren, die jeweils ausgehend von s(t), i(t) und r(t) iterativ die Werte nach einem kleinen Zeitschritt Delta t berechnen. Die Veränderungen lauten dann:
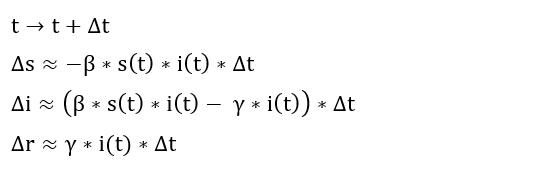
Änderungen der Funktionswerte bei kleinen Zeitschritten
Wir hatten bereits die Basisreproduktionszahl als das Verhältnis der Neuinfizierten zu den Genesenen (bzw. nicht mehr Infektiösen) berechnet. Hier gibt es eine ähnliche Berechnungsmöglichkeit, indem ich für einen kleinen Zeitraum Delta t die durch Ansteckung dazugewonnenen Infektionen ins Verhältnis zu den entfernten Infektionen setze:
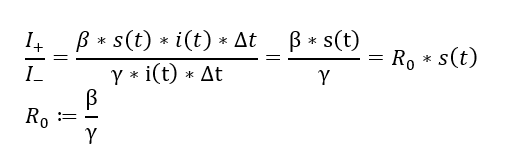
Quotient aus neuen und entfernten Infektionen in einem kleinen Zeitraum
Wie man sieht, kürzt sich da einiges weg. Eine Nebenbedingung war, dass wir uns am Anfang einer Epidemie befinden, sodass S = s(0) ungefähr 1 ist. Der Quotient aus Beta und Gamma ist nun die Basisreproduktionszahl R0. Ist dieser Quotient > 1, kommen anfangs somit mehr neue Infektionen zustande als Infektionen aufhören – die Infektionen nehmen somit zu, die Epidemie startet! Ist der Quotient bereits zu Beginn < 1, stirbt die Infektionskette von selbst aus.
Später in der Epidemie kann der Quotient aus Infektionszugängen und -abgängen selbst bei R0 > 1 kleiner als 1 sein, auch ohne Maßnahmen!
Dass die effektive Reproduktionszahl dann kleiner als eins sein kann, ist allein der Tatsache geschuldet, dass die zur Verfügung stehenden Empfänglichen S = s(t) abnehmen und nun nur noch in zu geringer Zahl vorliegen. Dies geschieht dann, wenn S = s(t) < 1 / R0 ist. Da S = 1 – I – R ist, ist das gleichbedeutend mit dem Sachverhalt, dass die aktuell Infizierten und die bereits abgeschlossenen Fälle zusammen einen Anteil von mindestens 1 – 1 / R0 = (R0-1)/R0 haben müssen. Dies ist die berühmte Schwelle zur Herdenimmunität.
Das RKI nennt Werte für R0 zwischen 2 und 3.3. Mit diesem Intervall ergäbe sich eine Herdenimmunität bei mindestens 50 % bis höchstens 70 %.
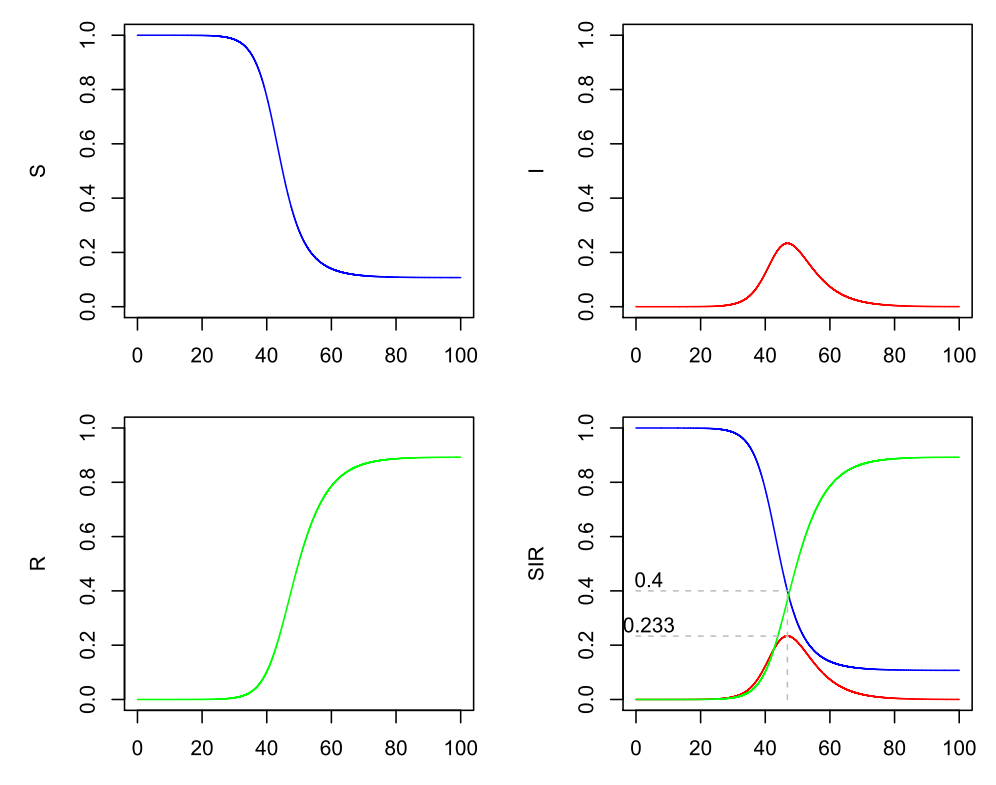
Nehmen wir mal ein R0 = 2.5 an. Beispielsweise ergibt sich dieser Quotient bei einer durchschnittlichen Dauer der Infektiosität von 5 Tagen (Gamma = 1 / 5 = 0.2) und einem Beta = 0.5, da 0.5 / 0.2 = 2.5 ist. Es ergibt sich dann der Verlauf, der bereits in der ersten Abbildung gegeben ist, aber hier noch einmal erscheint, damit Sie nicht scrollen müssen:
SIR-Modell (Beta=0.5, Gamma=0.2)
Ein paar interessante Beziehungen lassen sich ableiten; diese werden im Vorlesungsskript, das am Ende des Blogbeitrags genannt wird, erwähnt.
Beispielsweise lässt sich der momentane Anteil I als Funktion des momentanen Anteils S berechnen. D. h., kennt man S, kennt man auch I, und man muss nicht wissen, welcher Zeitpunkt t vorliegt.
Da wir oben gesehen haben, dass die Infektionen steigen, solange R0*S > 1 ist, und fallen, wenn R0*S < 1 ist, kann man nun ausrechnen, bei welchem S das Wachstum von I beendet ist und I zu fallen beginnt, nämlich, wenn R0*S = 1 und somit S = 1 / R0 = 1 / 2.5 = 0.4 ist.
Nun lässt sich aus diesem S die maximale Höhe von I ausrechnen (siehe Abschnitt 2.4.1 im Skript):
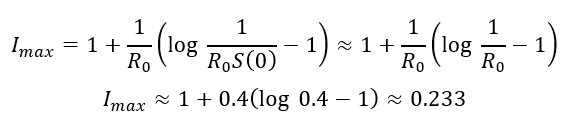
Maximaler Anteil an Infizierten (R0=2.5, Beta=0.5, Gamma=0.2)
Es gibt somit einen Zeitpunkt, an dem gleichzeitig 23.3 % der Bevölkerung infiziert sind.
Interessant ist, dass die genauen Werte von Beta und Gamma keine Rolle spielen, nur der Quotient, also die Basisreproduktionszahl R0 geht ein. Beim höchsten vom RKI angegebenen Wert 3.3 ergibt sich eine maximale Spitze der Infizierten von 33.5 %, bei dem kleinsten Wert 2 beträgt die maximale Spitze 15.3 %.
Möchte man nicht, dass die Zahl der gleichzeitig Infizierten so groß wird, braucht man somit ein kleineres R0.
Seit einiger Zeit wird versucht, durch NPI (non-pharmaceutical interventions) das R0 künstlich zu senken. Während eine Impfung direkt am Anteil S ansetzt und diesen verringert, wirken wir bei den NPI eher auf die Parameter des Modells ein, also auf Beta und Gamma.
Da das Gamma eine eher unveränderliche Eigenschaft der Krankheit ist, wird – in unserem Modell! – bevorzugt am Beta hantiert, das gesenkt werden soll.
Häufig wird dieser Parameter in ein Produkt weiterer Parameter zerlegt, die Kontakthäufigkeit pro Zeiteinheit oder Ansteckungsrate bei Kontakt oder ähnliche Größen berücksichtigen, um auch im Modell feiner steuern zu können. Durch Kontaktbeschränkungen wird dann die Kontakthäufigkeit gesenkt und ein Mundschutz verringert vielleicht die Ansteckungsrate eines Kontaktes.
Da hier natürlich die Bevölkerung mitspielen muss, sind exakte Vorhersagen schwierig, aber momentan scheint sich die aktuelle effektive Reproduktionszahl knapp unter 1 zu befinden.
Alternativ versucht man langfristig, durch Impfungen den Anteil von S künstlich zu senken, am besten unter die Schwelle der Herdenimmunität.
Mit dem Erreichen der Herdenimmunität hören die Infektionen im Modell ohne Maßnahmen übrigens nicht abrupt auf, sondern sie laufen aus. Es bleibt ein gewisser Anteil an S übrig, der wohl nicht mehr infiziert wird. Kann man diesen Anteil im SIR-Modell berechnen? Es entsteht eine transzendente Gleichung, die nur numerisch gelöst werden kann. Hier bleiben auf Dauer etwa 10.7 % von der Infektion verschont (siehe blaue Kurve für S). D. h. bei diesem Beispiel aber auch, dass zwar bei S = 40 % die Herdenimmunität einsetzt, aber trotzdem noch weitere 29.3 % der Bevölkerung im Laufe der Zeit infiziert werden.
Die Logik ist hier eher, dass ein Staat, der es bis zur Herdenimmunität geschafft hat, auch das Kommende bewältigen wird, da das Schlimmste überstanden ist. Natürlich ist die Abkürzung über eine Impfung mit einer genügend großen Anzahl an Freiwilligen der einfachere Weg. Die Infektionen streben übrigens langfristig immer gegen null.
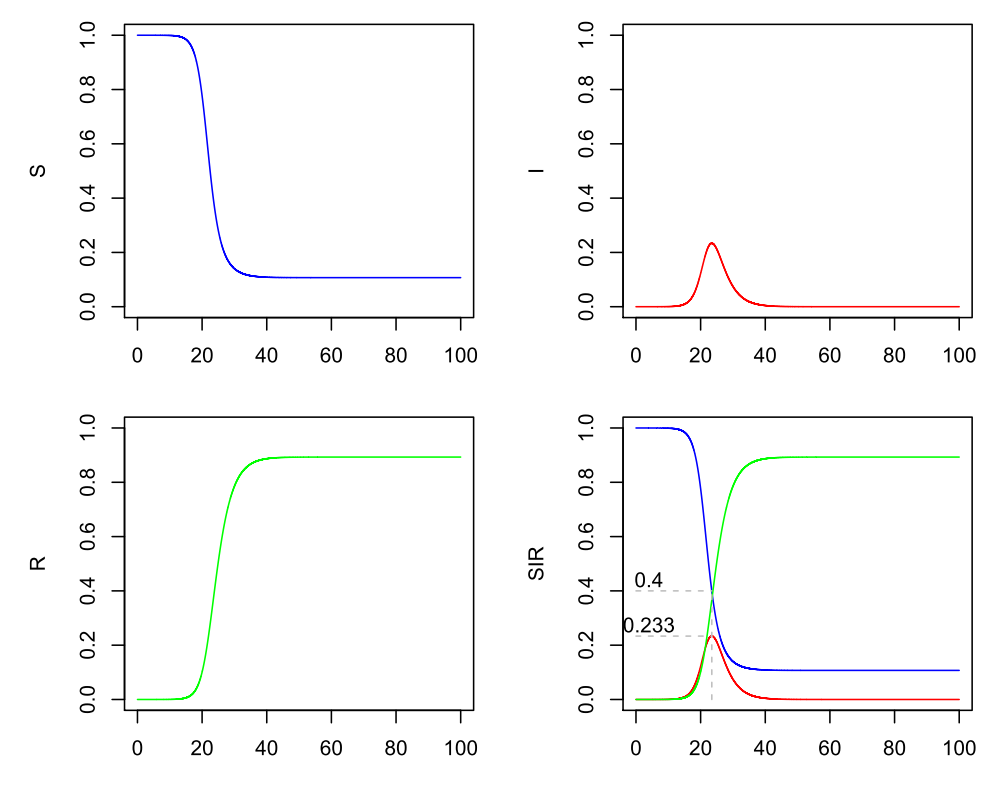
Nehmen wir mal an, dass es Methoden gibt, die das R0 gut schätzen, aber dass Beta und Gamma noch unsicher sind. Wenn Gamma etwa 0.4 ist (dies entspricht einer durchschnittlichen Infektiositätsdauer von 2.5 Tagen), also doppelt so viel wie oben angenommen, müsste Beta = 1 sein, um dieselbe Basisreproduktionszahl 2.5 zu erhalten:
SIR-Modell (Beta=1, Gamma=0.4)
Am Maximalanteil der Infizierten hat sich wie erwartet gemäß der Formel nichts geändert, aber jetzt läuft die Entwicklung auch doppelt so schnell ab. Das lässt sich auch über die Differentialgleichungen nachweisen.
Wenn ein Infizierter die gleiche Gesamtanzahl von Menschen anstecken muss, aber nur noch die halbe Zeit dazu hat, ist diese Beschleunigung logisch. Die Größe R0 allein beschreibt also nicht die gesamte Dynamik des Prozesses, sondern ist nur ein Baustein. Mit Festlegung von R0 wird sozusagen ein generisches Modell erstellt, das aber noch in der Zeit gestaucht (kurze Dauer der Infektiosität) oder gestreckt (lange Dauer der Infektiosität) auftreten kann.
Wenn man wissen will, wie sich denn die Maßnahmen auf die Infektionszahlen zum gegebenen Zeitpunkt auswirken, müsste man wissen, wo wir denn bezüglich der Anteile S, I und R stehen. Hierzu wären mal wieder repräsentative Stichproben notwendig!
Nehmen wir mal an, dass sich die absolute Anzahl für I (laut RKI-Situationsbericht vom 28.4.2020) etwa zu 33.000 (= 156.337 Gesamtfälle – 5.913 Verstorbene – 117.400 Genesene) und R(emoved) zu 5.913 + 117.400 ~ 123.300 berechnen lässt. Jeder Infizierte, solange nicht für gesund erklärt, wird als ansteckend interpretiert. Die Anzahl der Genesenen selbst ist auch nur geschätzt, da Genesungen nicht meldepflichtig sind.
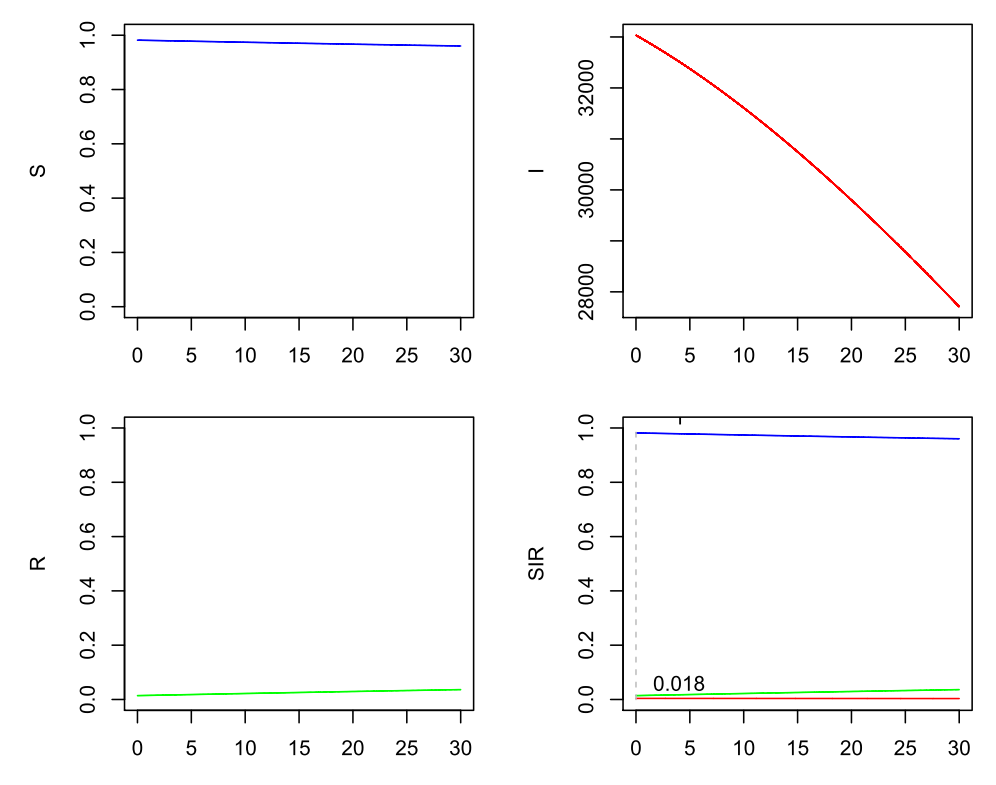
Wegen einer möglichen Dunkelziffer multiplizieren wir die Infizierten großzügig mit 10 (hier müsste man etliche plausible Konstellationen durchspielen!), landen also bei einer Startverteilung von i(0)=330.000/83.000.000 ~ 0.003975. Für R multiplizieren wir nur die Genesenen mit 10 und erhalten ungefähr r(0) ~ 1.179.913/83.000.000 ~ 0.0142. Daraus ergibt sich für den Rest s(0) ~ 0.9818. Würde ein R0 von 1 vorliegen, also das effektive R = R0*s(0) anfangs mit 0.9818 bereits leicht unter 1 liegen, ergäbe sich bei einem angenommenen Gamma = 0.2 und dem daraus resultierenden Beta = 0.2 der folgende Verlauf (hier sind bei I absolute Zahlen angegeben, die die sichtbaren 10 % der Infizierten zeigen!):
SIR-Modell (Beta=0.2, Gamma=0.2), s(0)=0.9818, i(0)=0.00398, r(0)=0.0142, 10 % sichtbare Infizierte
Hier sollten (gemäß Modell!) in einem Monat die sichtbar Infizierten von 33.000 auf ca. 28.000 gefallen sein. Bei einem noch kleineren R0 = 0.75 landet man in einem Monat sogar unter 7.000.
Hierbei ist den Infizierten bei Auftreten von stärkeren Symptomen eigentlich bewusst, dass sie infiziert sind und sie werden isoliert. Es ist also anzunehmen, dass die Neuinfektionen hauptsächlich stattfinden, bevor die ersten Symptome auftreten oder höchstens noch durch die Kandidaten mit leichteren Symptomen oder vielleicht noch durch die asymptomatischen Infizierten entstehen.
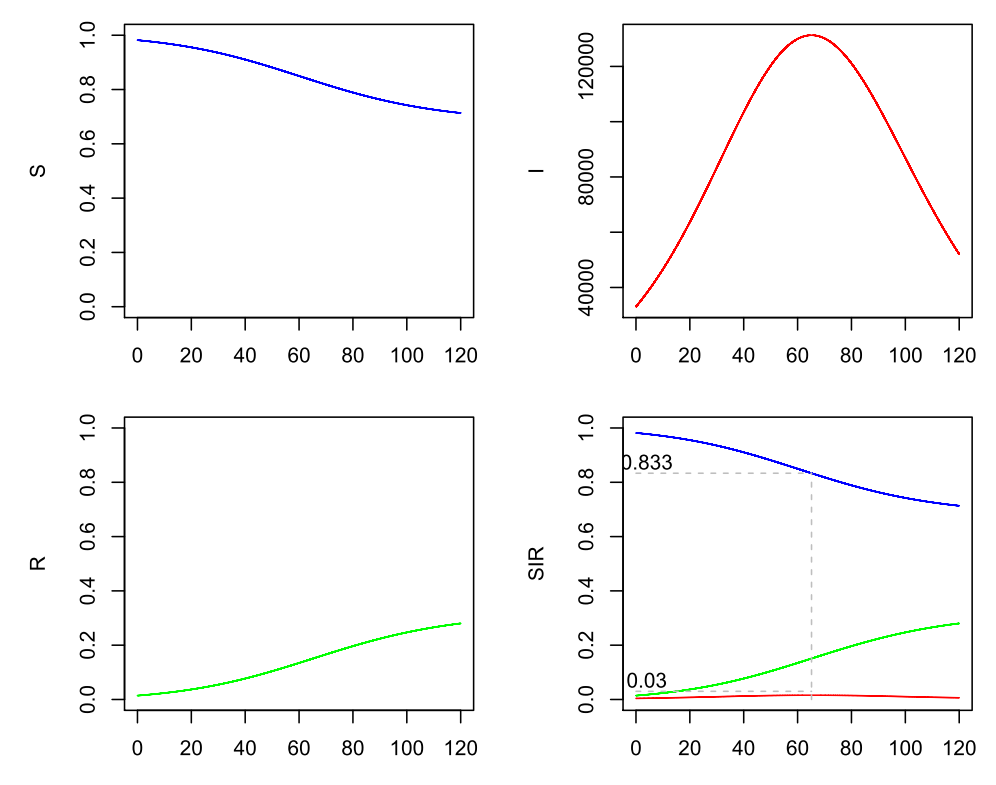
Was passiert bei Nachlässigkeit? Wäre R0 = 1.2, also das effektive R anfangs leicht über 1, so sähen die Verläufe so aus (man beachte die veränderte Zeitachse!):
SIR-Modell (Beta=0.24, Gamma=0.2), s(0)=0.9818, i(0)=0.00398, r(0)=0.0142, 10 % sichtbare Infizierte
Hier wäre dann nach ca. 65 Tagen das Maximum erreicht und die sichtbaren Infizierten liegen irgendwo bei 125.000.
Zur Erinnerung: Die Unsicherheit bei den Parametern kann mittels Bayesschen Ansätzen oder zumindest auf jeden Fall mit Monte-Carlo-Methoden berücksichtigt werden. Meine angenommenen Zahlenwerte sollen zwar nicht weit weg von den wahren Werten sein, dienen hier aber nur der Illustration der Methoden!
Das SIR-Modell ist nur das Einstiegsmodell der Epidemiologie; es gibt zahlreiche Erweiterungen.
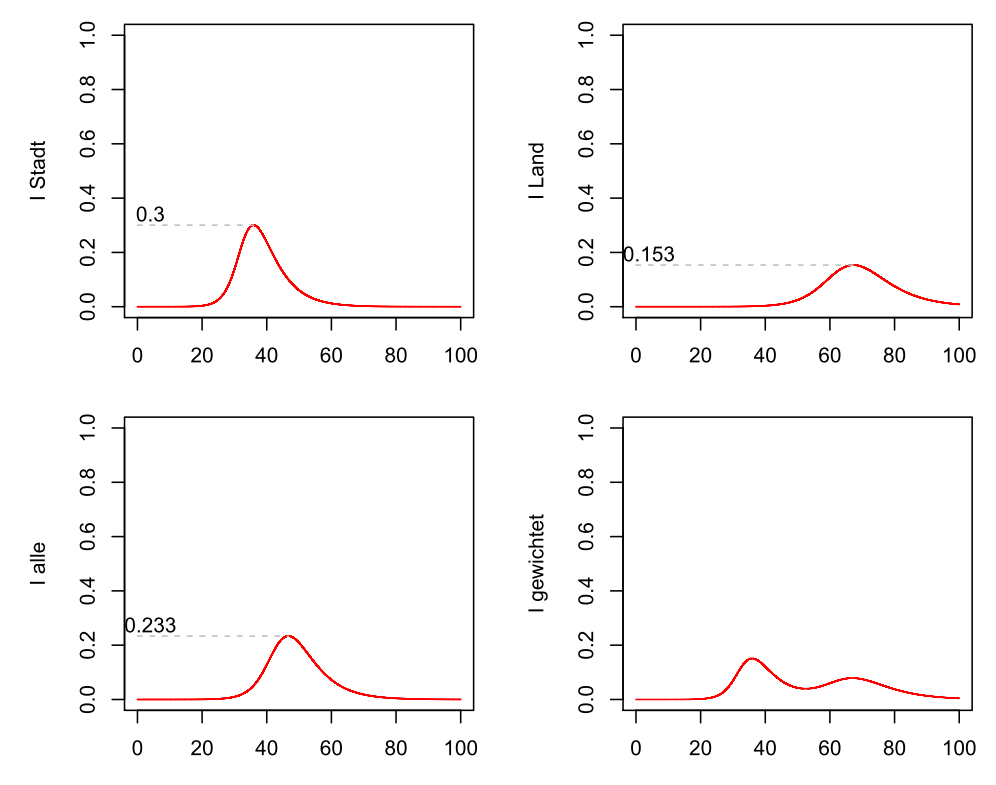
Beispielsweise könnten regionale Modelle erstellt werden, da sich höchstwahrscheinlich Land- und Stadtbevölkerung unterscheiden. Es wird hier sicherlich nicht ein einziges R0 geben.
Seien rein hypothetisch auf dem Land R0 = 2 und in der Stadt R0 = 3 zu beobachten, und beide Bevölkerungsteile sollen 50 Prozent ausmachen und sich normalerweise aus dem Weg gehen; wo ist dann der Unterschied zu einem einzigen umfassenden Modell ohne Differenzierung?
Hier würde man in getrennten SIR-Modellen wohl ein gemeinsames Gamma annehmen, aber unterschiedliche Betawerte. Ohne Differenzierung würde man bei diesen Annahmen ein R0= 2.5 für die Gesamtbevölkerung erhalten.
Entwicklung der Infektionen: Getrennte Modelle für Stadt und Land
Die Infizierten-Spitze fällt hier nur für die Stadt mit 30 % höher und nur für das Land mit 15.3 % geringer aus als die 23.3 % des Einheitsmodells. In der jeweils mit 0.5 gewichteten Summe ergibt sich der Verlauf der letzten Grafik mit lokalen Maxima, die aber durch die zeitliche Verschiebung immer unterhalb von 15.2 % liegen.
Für die gesamte Bevölkerung ist hier also die Prognose bezüglich der Infektionsspitze bei einem differenzierenden Modell nicht mehr so dramatisch, während das eine in diesem Beispiel betroffene Teilgruppe – nämlich die Stadtbevölkerung – wohl anders sehen wird.
Angemessen wäre hier auch noch das SEIR-Model, bei der zwischen S und I noch eine Exposed-Abteilung eingeschoben wird, die berücksichtigt, dass ein Infizierter eine Weile selbst nicht ansteckend ist. Aus den RKI-Angaben lässt sich eine mittlere Verzögerung von ca. 2.5 Tagen berechnen. Würde man also Exposed auch berücksichtigen, würde sich der Ablauf weiter verlangsamen, da infizierte Personen sozusagen erst einmal eine Zeit lang in einem Zustand ohne Einfluss verweilen, bevor sie wieder auf weitere Personen einwirken können.
Es kann auch sein, dass eine Immunisierung nur vorübergehend ist, und somit eine Verbindung von R zurück auf Start S existiert; es gibt Modelle, die asymptomatische Fälle behandeln.
In diesem vorläufigen Artikel Estimate of the development of the epidemic reproduction number Rt from Coronavirus SARS-CoV-2 case data and implications for political measures based on prognostics wird beispielsweise mit insgesamt 8 Abteilungen noch modelliert, wie Infizierte erkranken und ins Krankenhaus, bzw. sogar auf die Intensivstation müssen (siehe Bild 1 im zugehörigen PDF).
Die Wirklichkeit ist beliebig komplex und Modelle, die diese Wirklichkeit nachbilden wollen, können ebenfalls beliebig komplex werden, aber trotzdem können notwendige Bedingungen wie „das effektive R muss kleiner als 1 sein“ (sonst gehen die Infektionen nicht zurück) formuliert werden.
Das Hauptproblem für die Überprüfung der Wirksamkeit der momentanen Maßnahmen sind die Verzögerungen, die an verschiedenen Stellen vorliegen (z. B. bei den Meldungen). Die aktuellen Neumeldungen entsprechen eben nicht den Neuinfizierten dieses Tages (unabhängig von einer vorliegenden Dunkelziffer, die für die qualitative Entwicklung unerheblich ist, solange ein festes Verhältnis angenommen werden kann!), sondern beziehen sich durch Verzögerungen auf erkannte Infizierte der vergangenen Tage.
Dies heißt aber auch, dass die Zahlen der Infizierten in einem umgekehrten Verfahren aus den Meldungen geschätzt werden müssen. Da die Meldungen hinterherhinken, sind aktuelle Infiziertenzahlen nur Schätzwerte. Der dazu veröffentlichte Artikel des RKI hat wieder zu einigen nicht konsistenten Interpretationen geführt. Im Epidemiologischen Bulletin 17/2020 lassen sich Ansatz und weitere Quellen nachlesen.
Quelle:
Vorlesungsskript Modellierung mit Differentialgleichungen, Sommersemester 2019 von Lars Grüne, Mathematisches Institut, Fakultät für Mathematik, Physik und Informatik, Universität Bayreuth.