Oft ist es möglich, eine Menge von Objekten durch paarweise definierte Ähnlichkeiten (oder auch Unähnlichkeiten) zu beschreiben, die in einer Matrix dargestellt werden können. Wir präsentieren Ansätze, die Objekte derart zu ordnen, dass die Strukturen klarer hervortreten.
Als mögliche Anwendung ergibt sich beispielsweise die Darstellung des Zusammenhangs von Dimensionen in Gestalt des Kontingenzkoeffizienten, der von DeltaMaster z.B. in der Interdependenzanalyse verwendet wird.
In der Standardansicht geschieht die Darstellung tabellarisch. In der Matrixansicht erscheinen die Dimensionen sowohl in den Zeilen, als auch in den Spalten in der Reihenfolge, wie sie in der Sicht aufgeführt werden. Unabhängigkeit wird durch eine 0, starke Abhängigkeit durch eine 1 ausgedrückt. Wir haben es hier also mit einem Ähnlichkeitsmaß zu tun.
Die tabellarische Anordnung passt zur Anforderung, schnell eine Rangliste der stärksten Zusammenhänge zu erstellen; die graphische Darstellung als Matrix hilft, bei bekannter Reihenfolge der Dimensionen den Wert eines Zusammenhangs schnell nachzuschlagen, bzw. auffällige Werte einfach zu identifizieren.
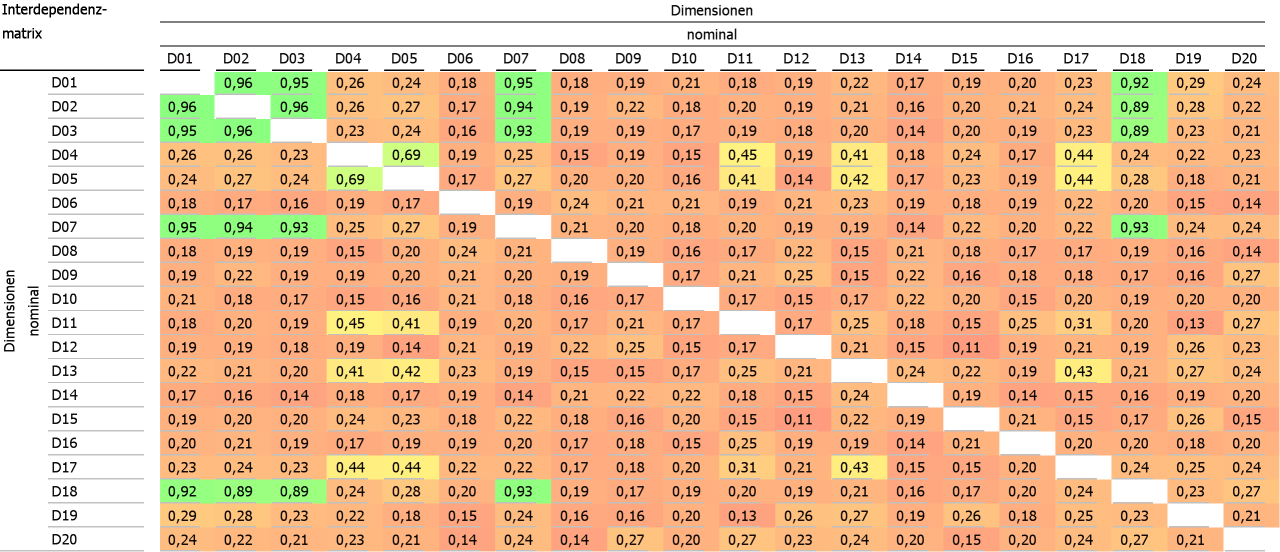
Die Abhängigkeiten zwischen den 20 Dimensionen
In einem Beispiel mit 20 Dimensionen könnte die Matrix wie in der obigen Abbildung aussehen (klicken Sie auf die Grafik für eine vergrößerte Darstellung!).
Wir möchten nun erreichen, dass wir einfacher erkennen, ob die Dimensionen Cluster bilden, d.h. ob die Dimensionen so gruppiert werden können, dass Dimensionen innerhalb einer Gruppe hohe Abhängigkeiten zeigen, die Zusammenhänge zwischen Dimensionen unterschiedlicher Gruppen jedoch geringer ausgeprägt sind. Diese Gruppen lassen sich in der obigen Darstellung noch nicht mühelos erkennen. Es gäbe nun zwar Möglichkeiten, diese Cluster in Bäumen darzustellen oder Projektionen über Multidimensionale Skalierung zu gewinnen, aber an dieser Stelle möchten wir innerhalb der Matrixdarstellung verbleiben.
Aber auch mit der Restriktion, sich auf Matrixdarstellungen zu beschränken, existieren noch einige Varianten. Allen ist gemein, die Dimensionen so anordnen zu wollen, sodass Dimensionen mit auffälligen Abhängigkeiten eng nebeneinander stehen. Die Anordnung wirkt sich natürlich immer simultan auf Zeilen und Spalten aus. Michael Hahsler und Kurt Hornik haben in ihrem Report (*) einige Algorithmen aufgeführt. Da sie von Unähnlichkeiten ausgehen, müssen die Werte unserer Matrix für die dort genannten Ansätze intern noch transformiert werden, am einfachsten durch f(x)=1-x. In unseren Grafiken werden aber immer die Originalwerte dargestellt.
Die aus einem Hierarchischen Clusterverfahren gewonnene Anordnung erzeugt das folgende Bild. Es ist nun z.B. leicht erkennbar, dass die Dimensionen 18, 7, 3, 1 und 2 einen Cluster bilden, in dem zwischen allen möglichen Paaren hohe Zusammenhänge vorherrschen. Gleichzeitig existiert ein zweiter Cluster mit ebenfalls 5 Dimensionen, der durch die Dimensionen 4 und 5 zusammengehalten wird.
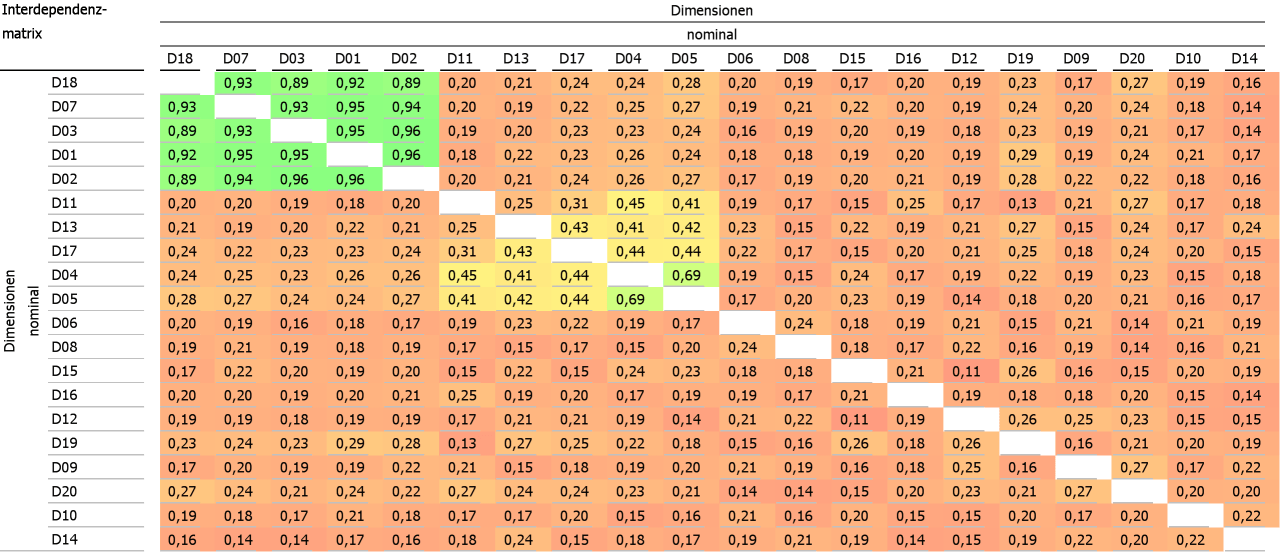
Sortierung mit Hierarchischem Clusterverfahren
Erstaunlicherweise lässt sich die Aufgabe auch als Problem des Handlungsreisenden (TSP: traveling salesman problem) darstellen: Jede Dimension stellt einen „Ort“ dar, und wir suchen eine möglichst kurze „Reise“, die jede Dimension einmal besucht, wobei „Entfernungen“ zwischen Dimensionen umso größer werden, je unähnlicher sich die Dimensionen sind. Wir benutzen dazu ein indirekt abgeleitetes Maß, das nicht die direkt aus der Matrix ablesbaren Werte benutzt, sondern auf den jeweiligen Abhängigkeiten gegenüber den restlichen Dimensionen aufbaut.
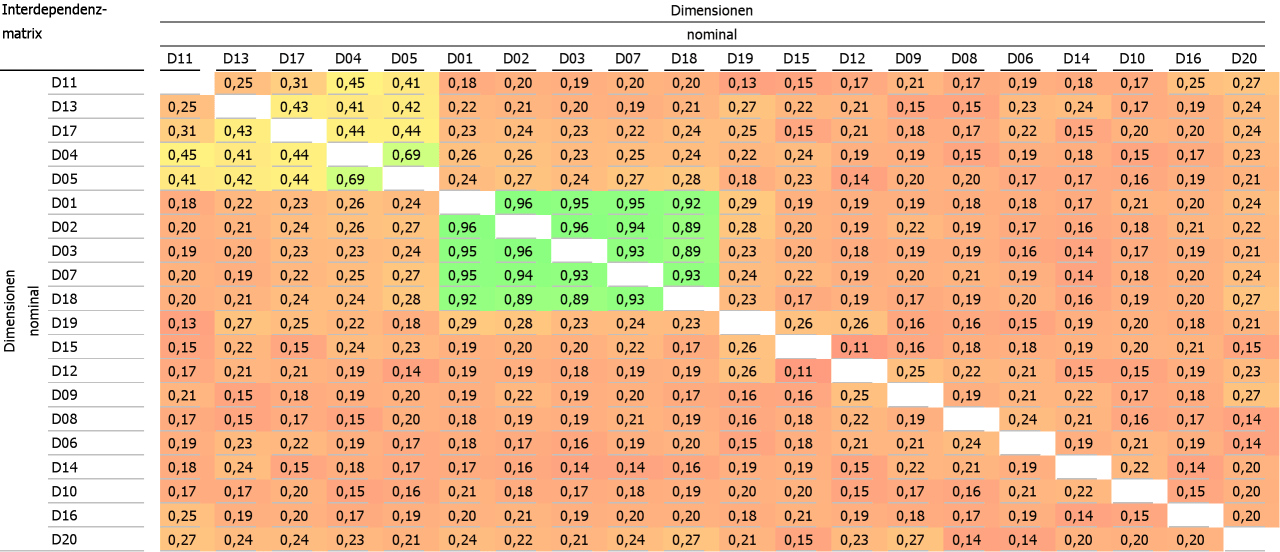
Sortierung mit TSP-Ansatz mit indirektem Maß
Grundsätzlich ergibt sich eine ähnliche Struktur wie mit der ersten Methode, mit den identischen zwei Hauptclustern. Wie sieht es bei einer größeren Anzahl von Dimensionen aus? Bei folgendem Beispiel sind die 85 Dimensionen in der Ausgangssituation bunt gemischt:
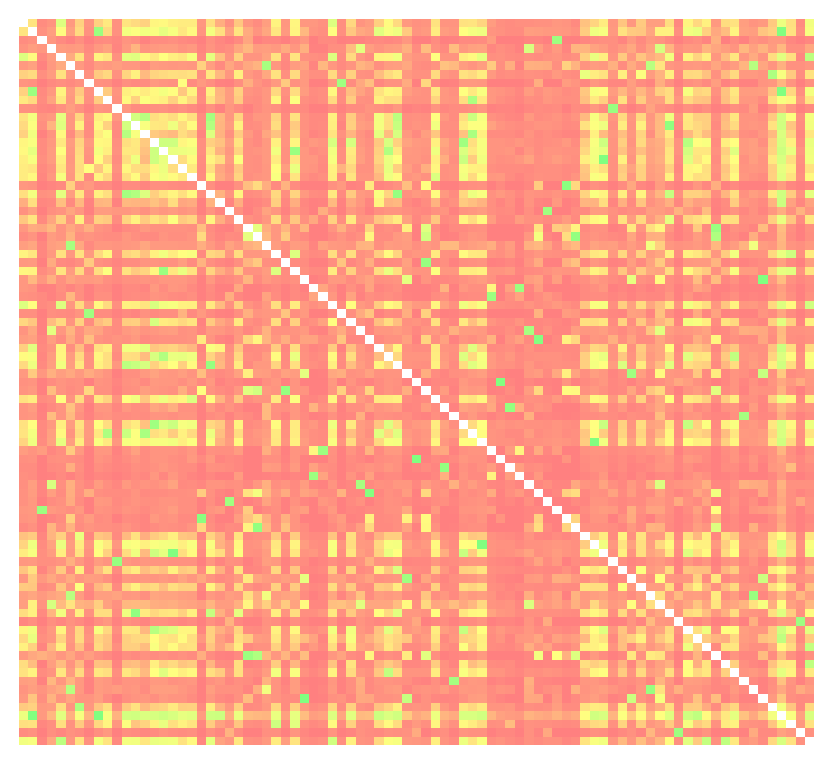
Original mit zufälliger Anordnung
Auch hier wird die Struktur durch die optimierte Anordnung der Dimensionen deutlich sichtbar:
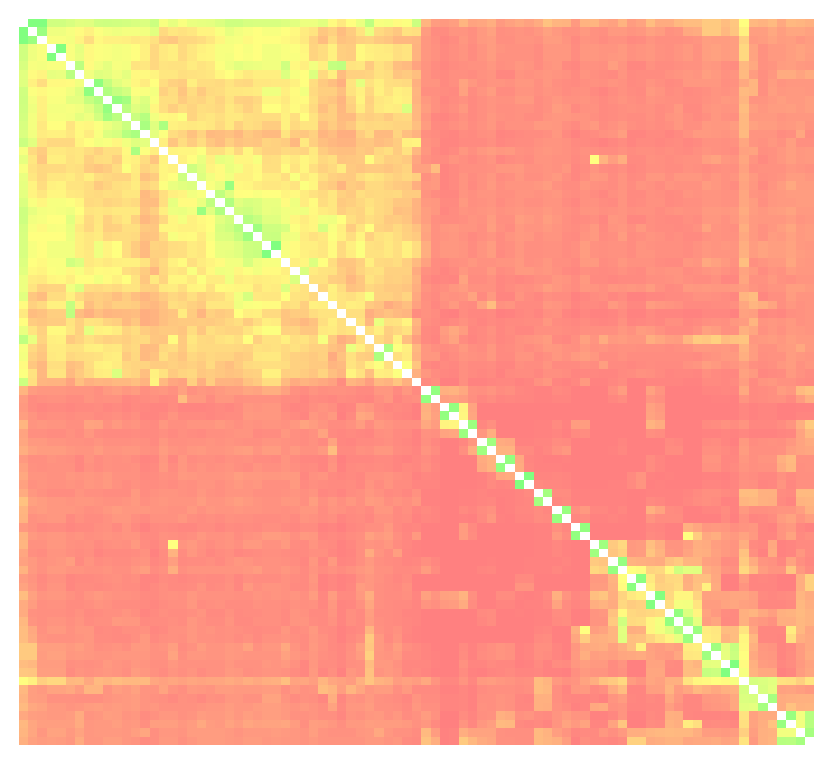
Optimierte Anordnung der Dimensionen mittels TSP-Ansatzes
Auffällig sind hier beispielsweise der Hauptcluster, der etwa die Hälfte der Dimensionen beinhaltet, und die vielen kleinen Cluster mit jeweils zwei bis drei Elementen. Weiterhin sind einige mittelgroße Cluster mit etwa vier bis neun Elementen erkennbar. Auch die einzelnen versprengten Pixel fallen nun auf, und die jetzt wahrnehmbaren „Linien“ sind ebenfalls einen zweiten Blick wert.
(*): Michael Hahsler, Kurt Hornik, „Dissimilarity Plots: A Visual Exploration Tool for Partitional Clustering“, Department of Statistics and Mathematics, WU Wirtschaftsuniversität Wien, Research Report Series Report 89, September
