Größen wie Erfolge oder Ausfälle werden häufig nicht absolut, sondern relativ als Anteile an einer Grundgesamtheit angegeben. Glücklich kann sich derjenige Anwender schätzen, der die zur Berechnung benötigten absoluten Anzahlen nicht voreilig entsorgt: Mit ihrer Hilfe sind tiefer gehende Analysen der Quoten möglich!

Stellen Sie sich bitte einmal vor, dass Sie einen Paketdienst für eine dringliche Lieferung beauftragen möchten. Der potenzielle Kandidat A hat bisher 4 von 6 und Kandidat B hat 60 von 100 Lieferungen innerhalb des Zeitfensters, das Ihnen vorschwebt, erfolgreich abgeschlossen. Wem würden Sie das Paket anvertrauen?

Zur Komplettierung des Feldes existieren weitere von Ihnen in jüngster Zeit beauftragte Kandidaten C und D. Die folgende Tabelle fasst die bisherige Erfolgsbilanz aller Kandidaten zusammen:

Erfolgsbilanz der vier Kandidaten, absteigend sortiert nach Quote

Schauen wir auf die nach der Quote der rechtzeitig eingetroffenen Lieferungen sortierte Liste, so führt Kandidat A mit 66.7 % die Liste an. Bei reiner Konzentration auf die Quote geht jedoch die Information verloren, auf welcher Grundgesamtheit dieser Wert beruht. Deshalb scheinen hier beispielsweise die Kandidaten B und D gleichwertig, obwohl sich doch Kandidat B bei gleicher Quote im Vergleich zu D bereits auf eine 5-mal größere Anzahl von Auslieferungen berufen kann. Für Kandidat C lässt sich hier bereits sagen, dass er bei der Auswahl B unterliegen wird, da er bei bei gleicher Gesamtanzahl weniger Erfolge aufweisen kann (C könnte aber trotzdem die höhere theoretische Erfolgsquote aufweisen, aber er wird bei rationaler Vorgehensweise nicht ausgewählt!).

Wie kann man berücksichtigen, dass Kandidat A mit bisher nur 6 Auslieferungen einer viel größeren Variabilität ausgesetzt ist? Hätte er nur ein einziges weiteres Paket nicht rechtzeitig abgeliefert, läge seine Quote nur bei 50 %. Bei Kandidat B hingegen führt ein weiterer angenommener Misserfolg anstelle eines Erfolgs nur zu einer Verringerung auf 59 %.

Wir versuchen es zunächst mit Konfidenzintervallen, die es in den Varianten exakt und approximativ gibt. Die Anwendung eines Konfidenzintervalls fußt auf der Annahme, dass es für jeden Kandidaten eine individuelle theoretische Erfolgswahrscheinlichkeit p der rechtzeitigen Auslieferung gibt. Die Anzahl der Erfolge ist dann binomialverteilt, mit individuellen Strichprobenanzahlen.

Der wahre Parameter p ist bei dieser Betrachtungsweise nicht zufällig – die Grenzen des Intervalls sind es! In Abhängigkeit der zufälligen Anzahlen für Erfolge bzw. Misserfolge wird ein somit ebenfalls zufälliges Intervall erzeugt. Die Konstruktion der Intervalle stellt sicher, dass die Wahrscheinlichkeit der Intervalle, die das p enthalten, mindestens einen vorgegebenen Wert 1-alpha erreicht und dies unabhängig vom wahren Wert von p! Für alpha=0.1 ergeben sich die folgenden unteren und oberen Grenzen der Konfidenzintervalle, berechnet mit der exakten Methode (das sogenannte Clopper-Pearson-Intervall).

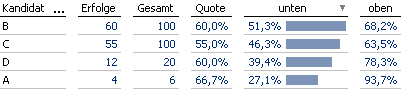
Absteigende Sortierung nach der unteren Grenze des Konfindenzintervalls

Nimmt man die untere Grenze des Konfidenzintervalls als Sortierkriterium her, so landet nun Kandidat A auf dem letzten Platz und B übernimmt die Führung. Je höher die Gesamtanzahl, desto schmaler das Intervall – deswegen entsteht hier der Vorteil für Kandidat B.

Bei einem Wert alpha=0.1 ist es nicht richtig, davon zu sprechen, dass das in der Tabelle gegebene, konkrete Intervall den wahren Parameter mit Wahrscheinlichkeit 0.9 enthält – der Parameter selbst ist bei dieser Sichtweise nicht zufällig und hat keine Verteilung. Wie bereits erwähnt sind nur die Intervalle zufällig.

Wäre es aber nicht schön, behaupten und belegen zu können, dass das p von B mit einer Wahrscheinlichkeit > 50 % höher ist als die Erfolgsquote von A? Was wir für solche Aussagen benötigen, ist eine Verteilung von p, d. h. wir möchten p als eine Zufallsvariable betrachten.

Es gibt nun einen Zweig der Statistik – die Bayes’sche Statistik – der genau solche Erweiterungen stützt und fördert. Für bestimmte Parameter, hier die Erfolgswahrscheinlichkeiten p, werden Verteilungen postuliert. Die beobachteten Daten werden dann benutzt, um über die Anwendung des Satz von Bayes aktualisierte Verteilungen der Parameter zu erhalten. Mit diesen A-posteriori-Verteilungen wird dann gerechnet.

Wo kommen nun die A-priori-Dichten der Verteilungen her? In der folgenden Grafik sind drei Varianten angegeben. Die einfachste Annahme geht davon aus, dass die Erfolgswahrscheinlichkeit p eines zufällig ausgewählten Paketdienstes zwischen 0 und 1 gleichverteilt ist (rot). Die grüne Dichte, die an den Rändern ansteigt, ist in einem gewissen mathematischen Sinne die optimale Wahl. Praxisnäher könnte die Schätzung der Verteilung der Erfolgswahrscheinlichkeiten eines zufällig ausgewählten Paketdienstes sein. Hier bei unserem Beispiel nehmen wir aufgrund unserer bisherigen langjährigen Erfahrungen mit anderen Paketdiensten an, dass typische Erfolgswahrscheinlichkeiten symmetrisch und konzentriert um 0.5 verteilt sind (schwarz):

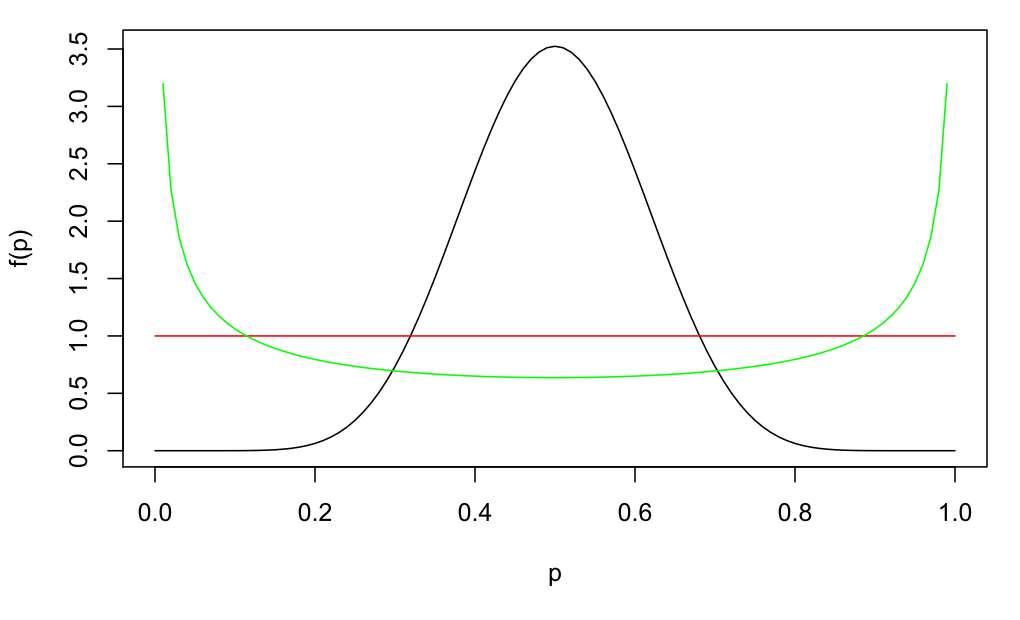
Drei mögliche Priors: einfach gleichverteilt (rot), mathematisch optimal (grün) oder subjektiv aufgrund Erfahrung (schwarz)

Wir entscheiden uns für die praxisnahe Variante (dies ist ein sogenannter subjektiver Prior, der trotz seines Namens so objektiv wie möglich gewählt wird) und verwenden für jeden unserer Kandidaten die schwarze Dichtefunktion. Die folgende Abbildung zeigt nun die aktualisierten A-posteriori-Dichten, hier für die Kandidaten A (grün) und B (schwarz), also die Dichten, die Vorwissen und die Erfolge und Misserfolge im konkreten Fall berücksichtigen:

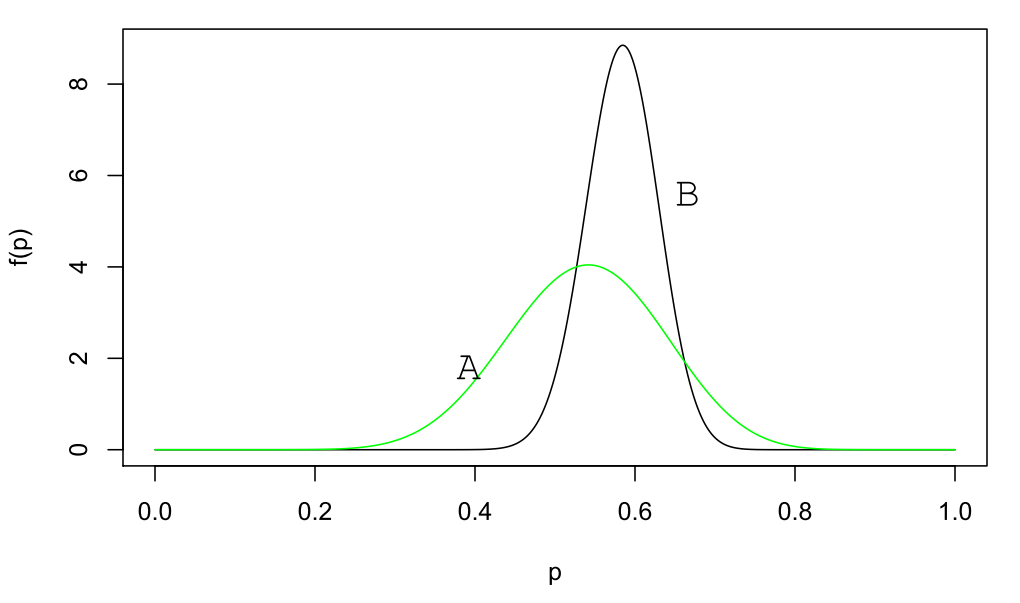
Die A-posteriori-Verteilungen für Kandidaten A und B

Verglichen mit dem Prior haben sich die A-posteriori-Dichten jeweils in Richtung der zugehörigen Quote verschoben. Je größer die Stichprobe ist, desto näher liegt der Schwerpunkt an der Quote und desto schmaler und höher wird auch die Dichte sein.

Mit diesen A-posteriori-Dichten können wir nun einiges anstellen. Um die vier Kandidaten sortieren zu können, sollten die Dichten auf jeweils eine Kennzahl eingedampft werden. Die Anzahl der spannenden Optionen ist nun eher gewachsen.

Fangen wir einfach an: Für jede Dichte kann die zugeordnete Erwartung berechnet werden, die natürlich möglichst groß sein soll.

Ein anderes Maß lässt sich aus einer möglichen Risikoaversion ableiten: Wir möchten das Risiko, dass der Kandidat schlechter als der Marktdurchschnitt abschneidet, minimieren, d. h. P(p>=0.5) soll möglichst groß sein.

Ein dritter Ansatz schaut eher auf die Chancen: Wir möchten uns die Möglichkeit offenhalten, einen absoluten Überflieger zu engagieren; dies soll bedeuten, dass wir P(p>=0.65) maximieren wollen. Es ergeben sich bei den drei Ansätzen die folgenden Werte:

Erwartung, Risikoaversion und Chance für die vier Kandidaten

Mit Kandidat B sollten wir einen guten Fang gemacht haben – er maximiert die Erwartung von p und auch die Wahrscheinlichkeit, besser als der Marktdurchschnitt abzuschneiden. Nur, wenn es um die Chance geht, haben Kandidaten A und D noch berechtigte Ansprüche, in die engere Auswahl zu gelangen. Bei ihnen besteht noch die größte Wahrscheinlichkeit, einen Schnellzusteller zu engagieren. Leider ist aber auch gleichzeitig die Gefahr, mit A und D lahme Enten zu erwischen, erhöht. Wie zu erwarten war, wird Kandidat C von B in allen Belangen dominiert.

Abschließend können wir auch noch die Wahrscheinlichkeiten berechnen, dass unser bevorzugter Kandidat B im paarweisen Vergleich eine höhere Erfolgswahrscheinlichkeit aufweist als jeder der drei Herausforderer. Jede der Erfolgswahrscheinlichkeiten p(A), p(B), p(C) und p(D) ist ja selbst eine Zufallsvariable, deren Verteilung jeweils durch die zugehörige A-posteriori-Dichte gegeben ist. Im direkten Vergleich ergeben sich die folgenden Werte: P(p(B)>p(A)) = 66 %, P(p(B)>p(C)) = 74 % und P(p(B)>p(D)) = 64 %.

Auch aus dieser Sicht liegen wir mit Kandidat B goldrichtig. Wir vertrauen unser Paket Kandidat B an!

PS: Übrigens könnten wir die in Damit es „Klick“ macht! gewonnenen Erkenntnisse der stetigen Webseitenoptimierung auch auf die Auswahl des Paketdienstes übertragen, um bei der Suche nach dem zuverlässigsten Anbieter so effizient wie möglich vorzugehen.