Wer die Wahl hat, hat die Qual – vor allem dann, wenn die Entscheidung zwischen zwei oder mehr Optionen wiederholt getroffen werden muss und die Konsequenzen zufälligen Einflüssen unterliegen. Sollte man häufig wechseln, um alle möglichen Varianten immer besser einschätzen zu können? Oder sollte man sich lieber schnell auf wenige oder gar nur einen Fall einschießen und dabei aber Gefahr laufen, auf lange Sicht nicht optimal zu handeln?
Entscheidungen unter Unsicherheit stellen ein faszinierendes und nahezu unerschöpfliches Forschungsgebiet dar. Aber selbst einfach anmutende Fragestellungen widerstreben manchmal hartnäckig einer offensichtlichen Lösung.
In unserem Fallbeispiel betrachten wir eine Webseite, auf der wir einen Link platzieren wollen, der mit einem Bild verschönert werden soll. Zur Auswahl stehen mehrere Bilder und wir möchten natürlich das optimale wählen, also dasjenige, das am häufigsten zum Anklicken verleitet und dann hoffentlich zum Kauf des auf der verlinkten Seite angebotenen Produktes führt. Die verlinkte Seite sei unabhängig vom gewählten Bild immer dieselbe und die anschließende Navigation sei vom Bild unbeeinflusst und kann deshalb für die Analyse vernachlässigt werden.
Welche Variante nehmen – mit Bild A oder mit Bild B?
Nehmen wir der Einfachheit halber einmal an, dass nur zwei Bilder A und B zur Auswahl stehen. Der Link wird bei Bild A wird in 20% aller Fälle angeklickt und bei Bild B in 60%. Leider sind diese Prozentzahlen zunächst unbekannt und können nur dann immer genauer bestimmt werden, wenn das entsprechende Bild immer wieder den Webseitenbesuchern präsentiert wird.
Die optimale Strategie bei Kenntnis der wahren Wahrscheinlichkeiten wäre hier natürlich, immer das Bild B anzubieten. Am Wert 60% müssen wir alternative Strategien messen. Wir tun dies, indem wir als Hauptkriterium den erwarteten Anteil der Klicks im Vergleich zur bisherigen Besucheranzahl hernehmen. Natürlich könnten wir zunächst Bild A 10000-mal präsentieren und anschließend Bild B 10000-mal und nehmen wir dann ab Besucher 20001 das Bild, das besser abgeschnitten hat, wird dieses mit sehr hoher Wahrscheinlichkeit Bild B sein. Leider haben wir bei diesem Vorgehen eine sehr hohe Anzahl von Klicks leichtfertig verschenkt.
Wir möchten also nicht unbedingt die tatsächlichen Klickraten aller möglichen Bilder bis auf die dritte Stelle hinter dem Komma ermitteln. Ständig muss abgewägt werden, ob das bisher vermeintlich beste Bild präsentiert werden sollte, um möglichst viele Klicks einzusammeln, oder ob vernachlässigte Bilder noch Potenzial besitzen könnten und deshalb präsentiert werden sollten, um ihre tatsächliche Performanz immer sicherer beurteilen zu können.
Betrachten wir einmal für unser Beispiel mit zwei Bildern eine Reihe von möglichen Strategien:
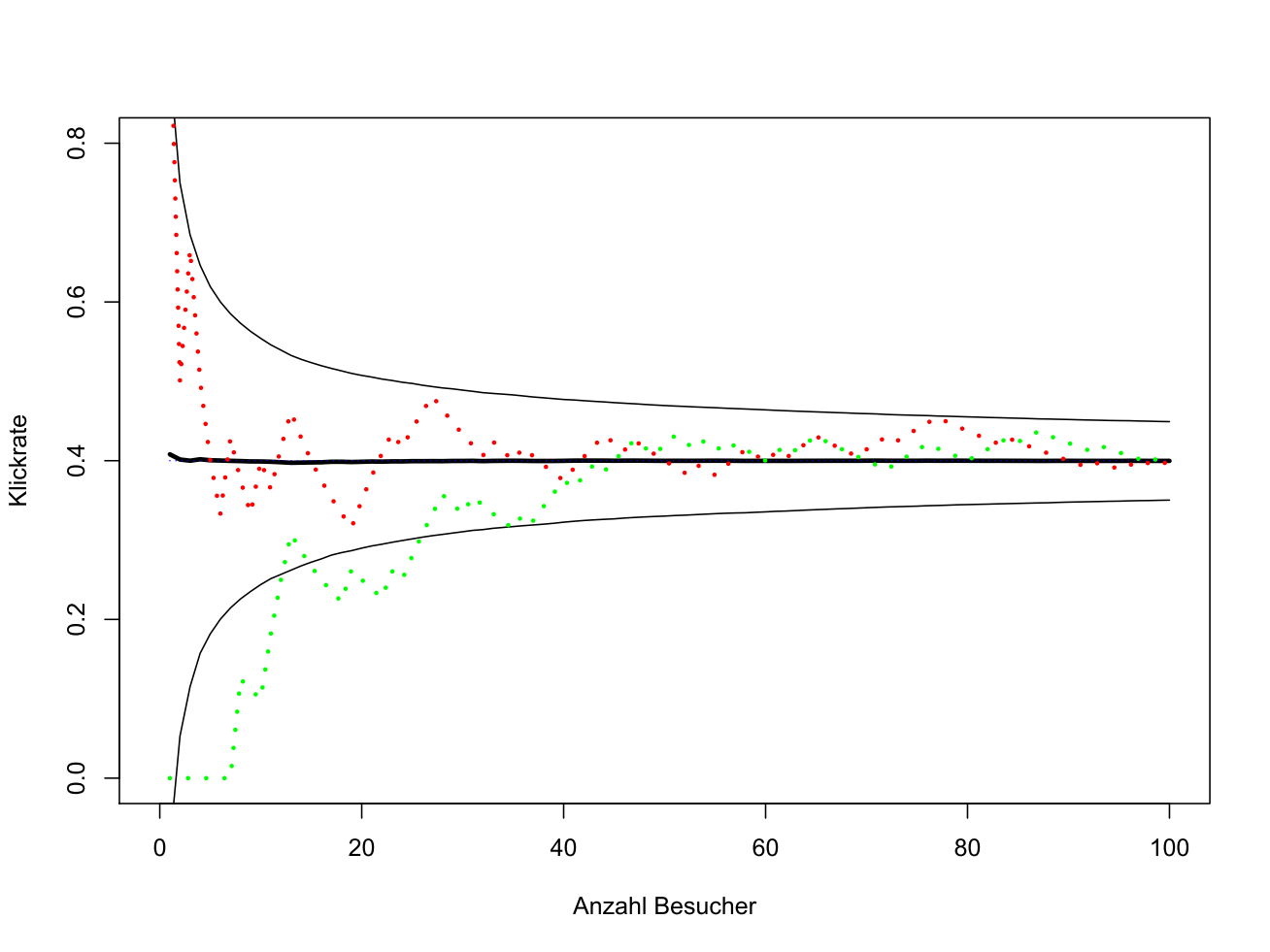
S1) Wir wählen immer eines der beiden Bilder zufällig mit p=1/2 aus. Mit Wahrscheinlichkeit 1/2 bieten wir pro Zeitpunkt das optimale Bild B an, mit gleicher Wahrscheinlichkeit 1/2 das unterlegene Bild A. Hier ist die erwartete Klickrate jederzeit 40%.
Wir nutzen Simulationen, um mögliche Verläufe der Klickraten zu illustrieren. 100 Personen besuchen der Reihe nach die Webseite und die Bilder A und B werden dynamisch mittels der genannten Strategie eingeblendet. Der gesamte Vorgang wird 10000-mal wiederholt. Die folgende Grafik zeigt das Ergebnis der Simulation (bitte klicken Sie auf die Grafik für eine vergrößerte Darstellung!):
Die durchgezogenen schwarzen Linien geben die mittlere, kumulierte Klickrate +/-Standardabweichung an. Die rote und die grüne gestrichelte Linie zeigen zwei mögliche Verläufe der 10000 Durchgänge. In der Anwendung wird man üblicherweise nur einen derartigen Durchlauf beobachten. Die empirische Klickrate kann sich also anfangs durchaus weit oberhalb oder unterhalb des erwarteten Wertes befinden, wird sich aber mit zunehmender Anzahl auf das Limit 0.4 einpendeln. Die erwartete Klickrate beträgt von Anfang an 40%. In nur etwa der Hälfte der Besuche wird das optimale Bild B präsentiert.
Es sollte bessere Strategien geben. Versuchen wir diese:
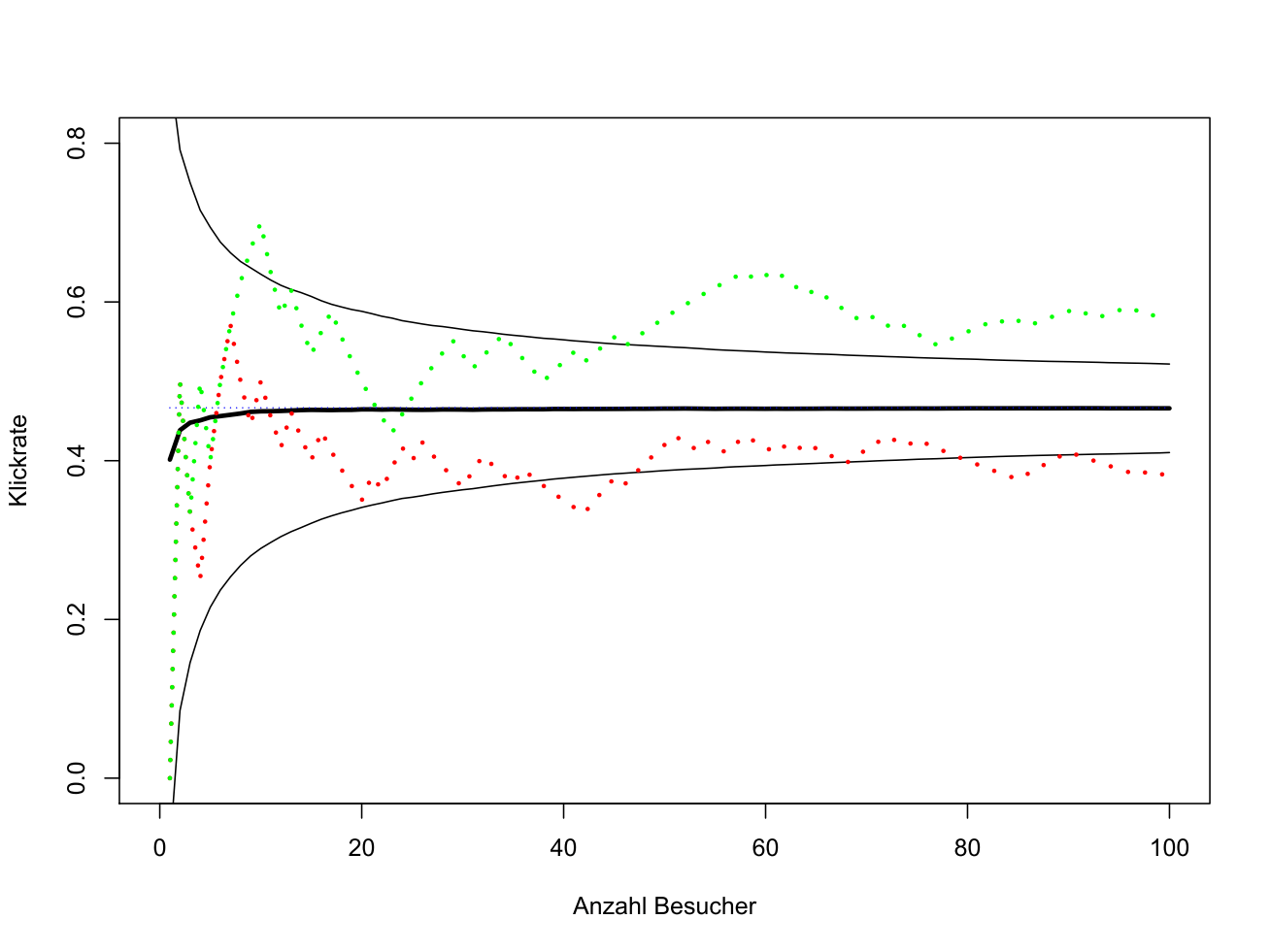
S2) Wir bleiben bei einem Bild, solange es angeklickt wird, und wechseln immer dann zur Alternative, falls dies nicht der Fall ist. Das erste präsentierte Bild wird zufällig ausgewählt.
Hier lässt sich eine Markov-Kette formulieren – Markov-Ketten waren bereits zweimal Thema dieses Blogs: So bekommt man Zustände und Serien mit Folgen – die die Übergänge zwischen den vier Zuständen „Bild A wird gezeigt und der Link angeklickt“, „Bild A wird gezeigt und der Link nicht angeklickt“, „Bild B wird gezeigt und der Link angeklickt“ und „Bild B wird gezeigt und der Link nicht angeklickt“ beschreibt.
Aus der Theorie der Markov-Ketten folgt ein Klickraten-Grenzwert von etwa 46.7% (zur Berechnung siehe (*)), der in der Erwartung relativ schnell erreicht wird (man beachte die Steigerung der durchschnittlichen Klickrate vom Startwert 40% innerhalb weniger Iterationen auf Werte nahe 46.7%) und eine Verbesserung gegenüber Strategie 1. Noch klafft jedoch eine gewaltige Lücke zum Optimum 60%.
Soll dieses Optimum erreicht werden, muss notgedrungen das Verhältnis der Anzahl der Kunden, die Bild A zu sehen bekommen, zu denen, die B sehen, im Laufe der Zeit gegen null streben. Diese Bedingung ist bei dieser Markov-Kette nicht erfüllt. Hier sehen etwa 2/3 der Besucher das gute Bild B, aber 1/3 bekommen weiterhin das unterlegene Bild A zu sehen, egal wie viele Besucher bereits die Webseite besucht haben.
Es muss also ein cleverer Ansatz her, wie etwa der in Chapelle et al. (**) beschriebene Algorithmus, der auf Bayes’schen Ansätzen aufbaut (die ihrerseits einmal einen Blogbeitrag wert wären!).
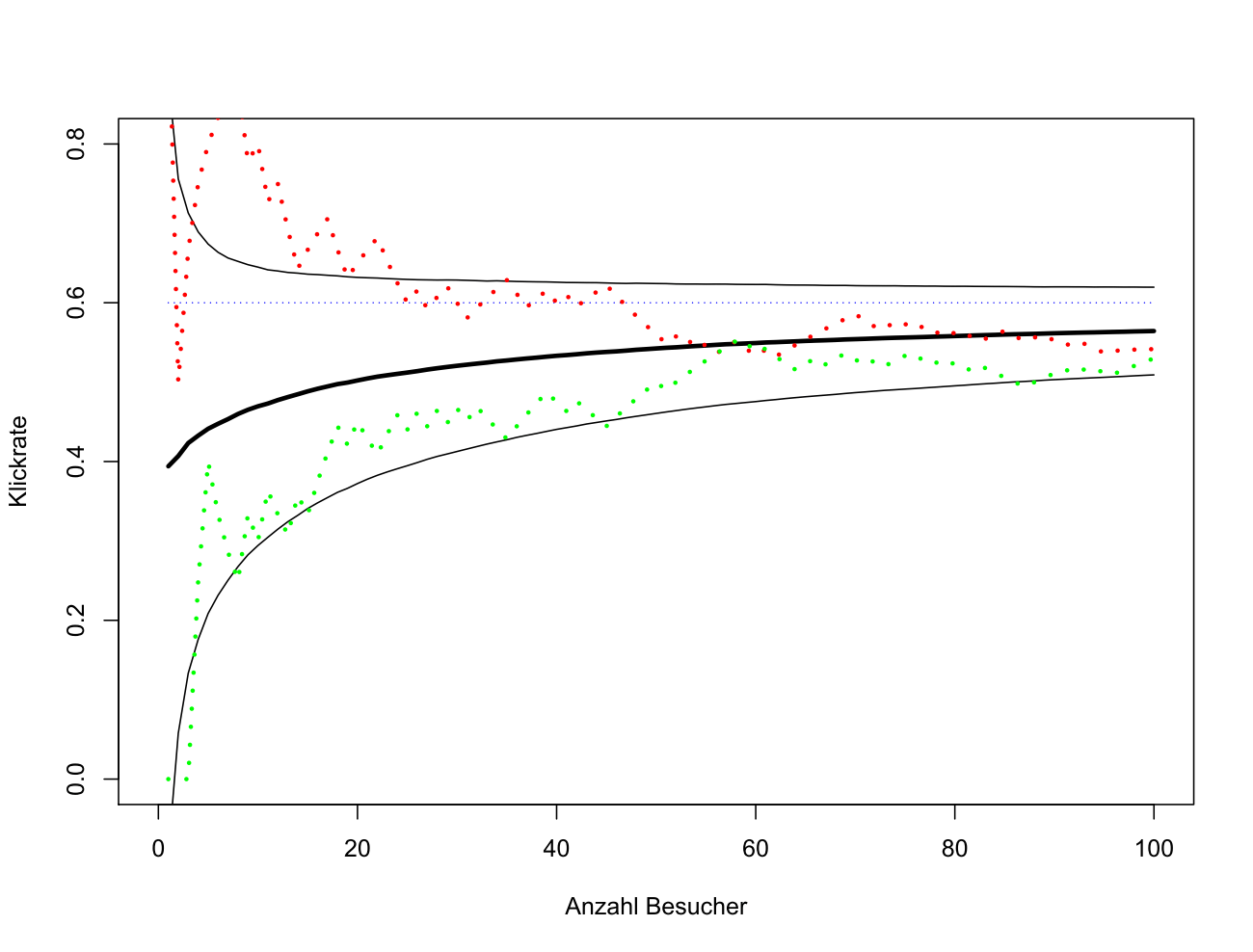
S3) Die möglichen Werte der Klickwahrscheinlichkeiten werden jederzeit durch eine Dichtefunktion angenähert, eine für Bild A und eine für Bild B. Zur Initialisierung dient jeweils eine Gleichverteilung auf dem Intervall zwischen 0 und 1, da anfangs für beide Bilder prinzipiell alle Werte gleichermaßen möglich sein sollen. Für jedes Bild wird jeweils aus der zugehörigen aktuellen Verteilung eine Zufallszahl gezogen und der größte Wert legt das gezeigte Bild fest. Anschließend wird geschaut, ob der Link angeklickt wurde oder nicht und die aktualisierte Verteilung wird als A-posteriori-Verteilung des gewählten Bildes gemäß den Bayes’schen Rechenformeln berechnet.
Die Dichtefunktion eines Bildes, welches häufig gezeigt wurde, wird schmal und hoch und verteilt ihre Masse konzentrierter um die wahre Klickwahrscheinlichkeit. Wurde ein Bild bisher wenig gezeigt, ist die Dichtefunktion eher breit, sodass die reelle Chance besteht, dass die Zufallszahl dieses Bildes die größte ist und somit das Bild ausgewählt und nicht vergessen wird.
Die Simulation zeigt, dass die mittlere Klickrate für die ersten 100 Besucher über alle Simulationsläufe hinweg etwa 56.5 % erreicht. Die mittlere Klickrate steigt dann mit jedem Besucher weiter, für die ersten 1000 Besucher ist sie mit ca. 59.5% schon sehr dicht an den optimalen 60%.
Nehmen wir nun zum Schluss in einem weiteren Beispiel an, dass vier Bilder mit den folgenden wahren, aber noch unbekannten Klickwahrscheinlichkeiten zur Auswahl stehen: A mit 0.9, B mit 0.7, C mit 0.4 und D mit 0.1.
Die folgende Grafik zeigt einen möglichen Verlauf für die ersten 100 Kunden und es ist ablesbar, welches Bild (A, B, C oder D) jeweils gemäß der Strategie 3 präsentiert wurde. Ein grüner Punkt markiert einen angeklickten Link, ein roter Punkt einen ignorierten Link.
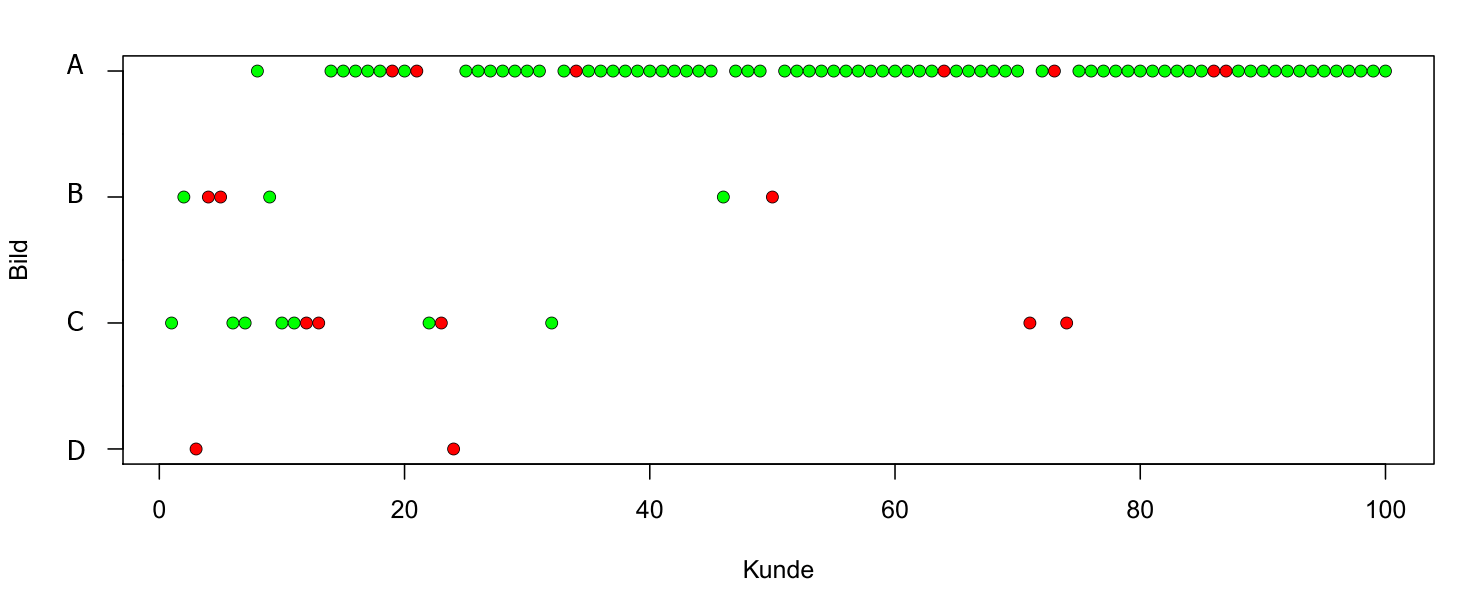
Simulation mit Strategie 3 bei vier Bildern
Es wird deutlich, dass das schlechteste Bild D insgesamt nur zweimal präsentiert und wegen mangelnden Erfolges bis auf Weiteres auf Eis gelegt wurde. Bild C startete trotz der relativ geringen Klickwahrscheinlichkeit von 0.4 mit fünf Erfolgen. Durch die anschließenden zwei Misserfolge von C bekommt das eigentlich beste Bild A die Gelegenheit, sich zu beweisen und wird dann bis auf wenige Ausnahmen durchgehend präsentiert.
Das angeführte Beispiel ist natürlich nur eines von vielen möglichen – es könnte bspw. auch um die Auswahl (nicht Generierung!) der eingängigsten Formulierung eines einleitenden Textes mit anschließendem Link gehen.
Es ist nicht trivial, Heuristiken zu entwickeln, die optimal im Sinne eines geeigneten Kriteriums sind, und es ist nicht einfach, diese Optimalität dann auch nachzuweisen. Je nach Zielkriterium wird sich auch die optimale Strategie ändern. Die Beschäftigung mit der Theorie der sequentiellen Entscheidungen unter Unsicherheit lohnt sich aber in jedem Fall – für den Intellekt und für die Firmenkasse.
(*) H. Robbins. Some aspects of the sequential design of experiments. Bulletin of the American Mathematics Society, 58:527–535, 1952.
(**) O. Chapelle and L. Li. An empirical evaluation of Thompson sampling. Advances in Neural Information Processing Systems 24, 2012.