Wenn in der Planung Stückzahlen auf prozentuale Zuschläge treffen, kann es schon einmal vorkommen, dass Planwerte unschöne Nachkommaanteile aufweisen. Wenn einfaches Runden nicht hilft, sondern eher Verwirrung stiftet, bedarf es eines Plans ℤ.
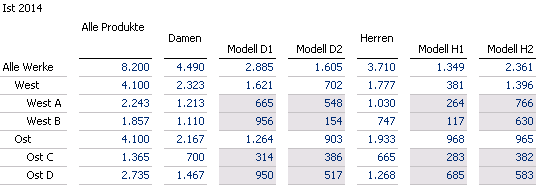
Nehmen wir in unserem konkreten Fallbeispiel an, dass in einer Schuhmanufaktur die Istwerte der Produktion des Jahres 2014 vorliegen:
Jeweils zwei exklusive Damen- und Herrenmodelle werden in insgesamt vier Produktionsstätten angefertigt. Die grau hinterlegten Felder stellen die Anzahlen auf den jeweils untersten Ebenen der beiden Dimensionshierarchien dar, aus denen sich die übrigen dargestellten Werte durch Aggregation ergeben.
Für das Jahr 2015 wird von einem Wachstum von 3 % ausgegangen und es ergeben sich die folgenden Planwerte:
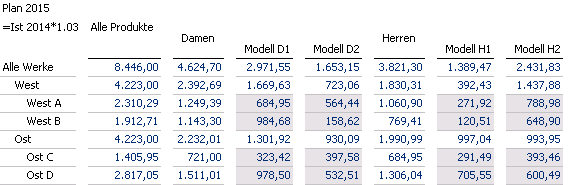
Ungerundete Stückzahlen Plan 2015
Der verantwortlichen Person tut es in der Seele weh, die exklusiven Schuhmodelle zerstückelt zu sehen, und sie möchte nur ganzzahlige Planwerte in der Tabelle betrachten. Leider führt der vermeintlich naheliegende Ansatz, alle Werte zellweise zu runden, zu Unstimmigkeiten (einen ähnlichen Fall hatten wir bereits in Abgerundet wird zum Schluss behandelt):
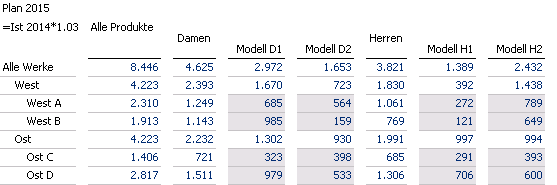
Plan 2015 Zelle für Zelle gerundet
Zum Beispiel gilt ungerundet für Herrenschuhe H2 im Osten zwar 393.46 + 600.49 = 993.95, aber Zelle für Zelle gerundet passt es nicht: Die Summe 393 + 600 ist leider nicht identisch zu 994.
Wir probieren einen Bottom-up-Ansatz aus und runden nur die Werte in den Basiszellen und berechnen die anderen Werte als Aggegration der gerundeten Werte:
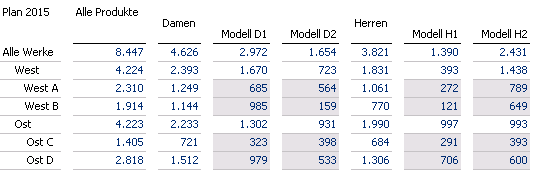
Plan 2015 aus den gerundeten Basiszellen aufaggregiert
Jetzt gehen zwar aufgrund der gewählten Vorgehensweise alle Summen auf, aber der Vorgabewert der Gesamtproduktion von 8446 wird um 1 verfehlt. In Abhängigkeit von der vorliegenden Datenkonstellation könnten hier aber auch größere Abweichungen entstehen. Hätten beispielsweise alle 16 Zellen einen Nachkommaanteil von 0.5, würden alle Basiszellenwerte aufgerundet werden und in der Gesamtsumme ergäbe sich eine unerwünschte Abweichung von 16 * 0.5 = 8.
Es ist an der Zeit, systematischer vorzugehen. Für unsere eingefärbten Basiszellen verlangen wir, dass die ganzzahligen Werte weniger als 1 von den ungerundeten Werten abweichen. Bereits ganzzahlige Werte bleiben unangetastet – die übrigen Werte werden entweder auf- oder abgerundet. Weiterhin soll die Gesamtsumme gleich der Vorgabe sein. Wie müssen wir vorgehen, um Abweichungen zwischen Summen von ungerundeten Werten und den Summen ihrer ganzzahligen Ersetzungen zu minimieren?
Es lässt sich leicht nachweisen, dass sich die Nachkommaanteile der Basiszellen des ungerundeten Planes zu einer ganzen Zahl S addieren lassen, die hier S = 0.95 + 0.68 + 0.42 + 0.50 + 0.44 + … + 0.46 + 0.49 = 10 beträgt. Damit die Gesamtsumme 8446 erzielt wird, müssen somit 10 von 16 Zellen aufgerundet werden und 6 abgerundet. Das ergibt im vorliegenden Fall „nur“ 8008 Möglichkeiten, aber welche Kombination sollte hiervon ausgewählt werden?
Lassen wir die aggregierten Werte zunächst einmal außer Acht und schauen nur auf die 16 Modell/Werk-Kombinationen auf der untersten Ebene. Aus diesen 16 Basiswerten können 2^16-1=65535 Teilmengen mit einem zugeordneten aggregierten Wert gebildet werden.
Für jede Teilmenge können wir die Summe der ungerundeten Werte mit der Summe der gerundeten vergleichen und den Absolutbetrag der Differenz der zwei Summen bilden. Die aggregierten Werte unserer Tabellen, die sich auf natürliche Weise aus den Hierarchien ergeben, sind Spezialfälle dieser größeren Menge. Beispielsweise ist 4626 im letzten Beispiel die Summe der acht Damenschuhfelder, die vom ungerundeten Wert 4624.70 um 1.3 abweicht.
Hier lassen wir jedoch völlig beliebige Teilmengen zu, die auch quer über die Hierarchien zusammengestellt werden könnnen. Es ist etwa erlaubt, die Anzahlen „Modell D2 in West A“ (564.44) mit „Modell H1 in Ost D“ (291.49) zu addieren und mit der ganzzahligen Summe zu vergleichen: |564.44 + 291.49 – ( 564 + 291)| = 0.93. Fügen wir „Modell H1 in West B“ (120.51) hinzu, erhalten wir für diese dreielementige Menge eine Abweichung von nur noch |564.44 + 291.49 + 120.51 – ( 564 + 291 + 121)| = 0.44
Haben wir festgelegt, welche 10 der 16 Basiszellen aufgerundet werden sollen, ergibt somit jede der möglichen 65535 Teilmengen eine bestimmte Abweichung. Gibt es unter den 8008 möglichen Zuordnungen eine ausgewählte, die uns generell vor besonders großen Abweichungen bewahrt, unabhängig davon, welche der Teilmengen betrachtet wird?
Von der Gesamtmenge, die alle 16 Zellen enthält, wissen wir bereits, dass die Abweichung 0 betragen wird, da wir ja genau 10 Zellen aufrunden werden. Für die 16 einelementigen Mengen haben wir eine maximale Abweichung < 1, da nur Auf -bzw. Abrunden zur nächsten ganzen Zahl erlaubt ist.
Für (mindestens) eine der 65535 Teilmengen wird hingegen die größte Abweichung gemessen. Wir möchten nun den Worst Case optimieren, d.h. eine solche Zuordnung der 10 aufzurundenden Zellen finden, dass die größte auftretende Abweichung minimiert wird. Die Berechnung der optimalen Zuordnung für die Worst-Case-Minimierung ergibt für unser Beispiel die folgenden gerundeten Werte:
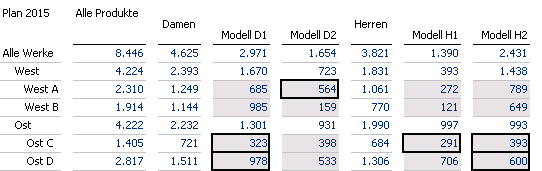
Plan 2015 mit Worst-Case-Minimierung
Es sind die Zellen markiert, die als Teilmenge die maximale Abweichung ergeben:
|564.44 + 323.42 + 978.50 + 291.49 + 393.46 + 600.49 – ( 564 + 323 + 978 + 291 + 393 + 600 )|= 2.8
Die gleiche Abweichung ergibt sich übrigens auch für die Teilmenge der nicht markierten Zellen. Egal, welche der 65535 Teilmengen nun betrachtet wird – keine Summe wird mehr als 2.8 vom ursprünglichen Wert abweichen. Sind wir somit am Ziel? Dies verneinen wir leider:
Der gezeigte Ansatz sichert uns für beliebige Teilmengen gegen zu große Fehler ab, aber die aggregierten Werte, die in der Tabelle erscheinen, sind nicht ohne Grund angegeben. Besonders hier wünschen wir kleine Abweichungen. Beispielsweise weichen die Planwerte 2015 für West und Ost voneinander ab, obwohl doch die Istwerte 2014 noch identisch waren.
Es ist also wünschenswert, bestimmte Aggregationen (= ausgewählte Teilmengen der Basiszellen) bevorzugt zu behandeln, während trotzdem die Fehler auf den restlichen möglichen Kombinationen möglichst klein bleiben sollen.
Hier in diesem Beispiel bietet es sich an, mit einem Top-down-Ansatz einen optimalen aggregierten Plan nur für die 4 Werke und die 2 Regionen zu erstellen. Der Gesamtplanwert wird in vier optimal gerundete ganzzahlige Werte für die Werke zerlegt:

Ganzzahliger optimal gerundeter Plan 2015 für die Werke
Die vier ganzzahligen Werte der Werke dienen nun als Vorgabe, um jeweils einen Worst-Case-optimierenden Teilplan für die Basiszellen der jeweiligen Zeile zu erstellen. Zum Vergleich noch einmal die Ausgangssituation:

Ungerundete Stückzahlen Plan 2015
Und hier der passende ganzzahlige Plan, der über die Werksdimension das Ausgangsproblem in vier Teilprobleme zerlegt:
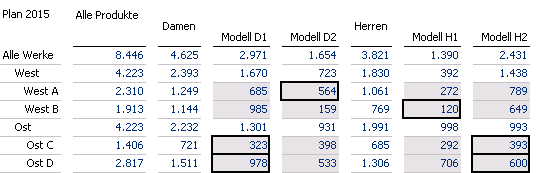
Ganzzahliger Plan 2015 unter besonderer Beachtung der Randsummen der Werksdimension
Hier ist der Worst Case mit 2.82 gegeben – er hat sich also nur um 0.02 erhöht. Sämtliche sichtbaren aggregierten Werte sind nun aber maximal 0.96 (Wert für Modell H1/Ost) von den ursprünglichen, ungerundeten Werten entfernt – die meisten sogar weniger als 0.5. Dies ist nicht die einzige Möglichkeit, das Ausgangsproblem zu vereinfachen. Man hätte beispielsweise auch die Produkthierarchie nehmen oder den Gesamtwert in vier Region/Geschlecht-Kombinationen zerlegen können.