In the previous parts of this series (iPod, PowerSearch) I demonstrated how simple rankings can deliver much more information than initially meets the eye. Let’s take another look at our Formula 1 data, but this time we will create a ranking across all data and simultaneously search for unusual combinations of characteristics. After all, Formula 1 is just one of many sports in which several different factors determine the winner. Grant it, our data doesn’t offer much detail in this aspect, but I’ll let that pass for the sake of a simple illustration.
The following list shows the results for double combinations:
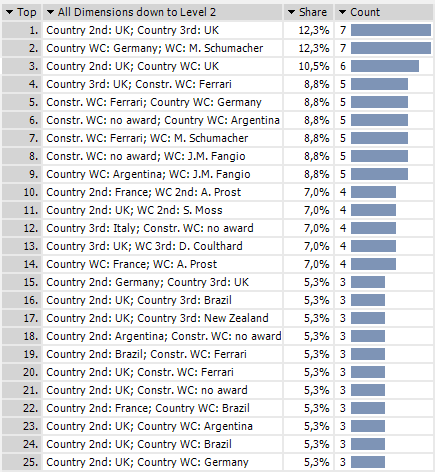
Within the first two lines we can spot our first interesting relationship. The German pilot Michael Schumacher has won the world championship just as many times as British pilots have ranked second and third within a single season.
British pilots have also won the champion and runner-up trophies in six separate seasons – not bad for a country where people still drive as they did in the days of horses and buggies…on the left side of the road! Ferrari, too, was most successful with Schumacher behind the wheel.
What is remarkable about this procedure is that you can apply it to almost any kind of question. The interesting criterion is always the measure by which you sort your data, whether you are dealing with simple revenue figures or complex Key Performance Indicators.
Of course, you don’t always have to go to extremes as done, for example, by a market research institute which recently conducted a passenger survey on quality in order to shape the profile of a major airline. An index was created based on the given point values and, in turn, was tested against all combinations of elements. Since the survey contained countless quality attributes and the airline included its own customer information, the final data model contained over 40 dimensions with almost 500 elements and several million characteristic combinations!
We can use simple rankings to explore complex relationships as in the example above. Whether you understand the results or not, however, ultimately depends on how well you understand the measure that serves as the basis for your ranking. And if you do, you know that you can trust the results, because you know how they were derived instead of blindly accepting the “black box” effect of many high-level data mining algorithms.
